Інтегрований урок з алгебри та інформатики при вивченні теми «Етапи статистичного дослідження. Завдання математичної статистики»
Імовірнісно - статистична змістова лінія має велику прикладну цінність. Йдеться про вміння аналізувати випадкові фактори, оцінювати шанси, висувати гіпотези, прогнозувати розвиток ситуації, використовувати статистичну інформацію і, нарешті, приймати рішення в ситуаціях, що мають імовірнісний характер, у ситуаціях невизначеності. Ймовірнісно - статистичне мислення необхідне людині для професійного становлення. Статистичні методи застосовуються для дослідження соціальних і економічних явищ, в астрономії, фізиці, біології, психології, мовознавстві тощо, ними найрізноманітніші явища- від явищ, що відбуваються в мікрочастинках, до явищ у людському суспільстві. Щоб професійна школа змогла ефективно сформувати вміння користуватися статистичними методами учні мають бути готовими до цього , мати уявлення про них, користуватись ними в найпростіших випадках. Необхідно учня сприймати і застосовувати статистичну інформацію. Тоді це може стати надбанням на все життя.
Тема уроку : Етапи статистичного дослідження. Завдання математичної статистики
( урок-практикум з алгебри та початків аналізу, 11 клас, ІІ курс)
Мета уроку:
Освітня: закріпити поняття математичної статистики як розділу прикладної математики; сформувати уявлення про види статистичних спостережень та основні етапи статистичних досліджень; формувати уміння учнів будувати частотні таблиці, гістограми, полігони на основі власноруч зібраних даних; знаходити центральні тенденції вибірки: середнє значення, моду, медіану.
Розвиваюча: розвивати способи і прийоми мислення, індивідуальні здібності учнів, їх пізнавальні інтереси.
Виховна: виховувати розумову культуру, культуру усного і писемного мовлення та міжособистісного спілкування.
Тип уроку: урок засвоєння нових знань та способів дій.
Обладнання: підручники, таблиці, опорні конспекти, інформаційні картки, бланки зібраної інформації для статистичного дослідження, листи для оформлення статистичних звітів груп.
Хід підготовки до уроку
- Учні групи об’єднуються в різнорівневі (за рівнем навчальних досягнень) експертні групи для спільного статистичного спостереження з подальшим опрацюванням на уроці. Учитель призначає керівника групи учня, який організовує і контролює діяльність усіх членів групи.
- Кожна група отримує своє завдання:
- зібрати дані про температуру за лютий місяць;
- зібрати дані про розмір взуття в групі;
- зібрати дані про зріст юнаків в групі;
- зібрати дані про вагу учнів в групі.
3. Для роботи на уроці кожній групі видається картка - інструкція, опорний конспект (додаток 1)., лист статистичного звіту учні (додаток 4)
Етапи уроку
- Організація класу.
2. Мотивація діяльності.
3. Пояснення нового матеріалу.
4. Формування навичок і вмінь.
5. Закріплення нових знань.
6. Домашнє завдання.
7. Підбиття підсумків уроку.
Хід уроку
1. Організація групи
До початку уроку учні розсаджуються по експертним групах.
2.Мотивація діяльності
Найкраще рішення у будь-якій ситуації можна прийняти лише тоді, коли є необхідна інформація. Майбутній робітник має розуміти, що якою б справою не займалась людина, часто змушена приймати рішення з урахуванням багатьох обставин, не маючи повної і точної інформації. Будь-яку інформацію слід використовувати якомога повніше. Статистичний аналіз допомагає здобувати інформацію із наявних даних і оцінювати якість цієї інформації в різних життєвих та виробничих ситуаціях.
Статистика (лат.status-стан, становище). Заслуховується повідомлення учня «З історії розвитку статистики» ( додаток 2)
3.Пояснення нового матеріалу
Учитель ознайомлює учнів з основними етапами статистичного дослідження:
- статистичне спостереження:
- статистичне зведення, групування;
- обчислення центральних тенденцій;
- побудова графіків (гістограм, полігонів).
- За таблицею «Статистичні спостереження» з’ясовуються види спостережень за трьома основними ознаками: часовою, за способом організації, за ступенем повноти охоплення одиниць.
Розв’язується задача, на прикладі якої вчитель пояснює основні етапи дослідження, вводить нові поняття, дає алгоритм виконання кожного етапу дослідження і зразок оформлення. Учні в зошитах ведуть записи таким чином: ліворуч розв’язання задачі, а праворуч означення нових понять, алгоритм виконання етапів дослідження.
Задача
За перший семестр учні отримали такі оцінки
Табл.1
|
№ за списком |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
Бали |
1 |
9 |
7 |
1 |
6 |
7 |
4 |
8 |
8 |
4 |
4 |
7 |
5 |
9 |
7 |
7 |
1 |
4 |
Розв’язання
- Статистичне спостереження: одиничне - за часовою ознакою(так як потрібне лише один раз для розв’язування задачі на уроці), звітне - за способом організації(так як дані взяті з журналу групи); несуцільне – за ступенем охоплення одиниць ( не беремо до уваги учнів, що прийшли в групу після 11 кл.)
- Статистичне групування: згрупуємо дані за досліджуваною ознакою – рівнем успішності учнів і запишемо їх у таблицю таким чином – табл.2
Таблиця 2.
|
Ознака-кількість балів |
1 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Частото-кількість учнів |
3 |
4 |
1 |
1 |
5 |
2 |
2 |
Таблиці такого виду називаються частотними. В ній перший рядок – параметри досліджуваної ознаки, а другий рядок – частоти, які показують, як часто зустрічається у вибірці її значення
Отже, статистичне групування оформлюється в частотні таблиці. Іноді потрібно знайти відносну частоту ознаки.
Відносна частота ознаки =(частота значення : загальну кількість знач)*100%
В нашій задачі відносна частота значення 9 балів дорівнює:
(2:18) 100%=11%
Отже, 11 % учнів групи засвоїли предмет на рівні 9 балів.
- На цьому етапі розглянемо центральні тенденції вибірки та алгоритми їх знаходження.
Середнім значенням вибірки називається середнє арифметичне усіх її значень.
Алгоритм знаходження середнього значення вибірки ( х )
- Знайти добутки значень вибірки на їх частоту.
- Скласти всі добутки ( одержимо суму всіх значень вибірки).
- Одержану суму поділити на загальну кількість членів вибірки
У нашій задачі:
Середнє значення (1*3+4*4+5*1+6*1+7*5+8*2+9*2)=99:18=5,5
Можна зробити висновок, що середній бал учнів 5,5.
Мода ( лат.modus – міра, правило) вибірки - це те значення ознаки, яке трапляється найчастіше, тобто має найбільшу частоту.
Алгоритм знаходження моди вибірки ( Мo)
- Знайти в рядку частот найбільше число (їх може бути декілька найбільших і рівних між собою).
- У рядку значень ознаки знайти відповідні значення, які відповідають найбільшій частоті або частотам.
Зауваження. Моди вибірки не існує, якщо всі значення вибірки зустрічаються однаково часто. Якщо два середніх сусідніх значення мають однакову частоту і вона більша від частоти буд-якого значення, то мода є середнє цих значень.
У нашій задачі найбільша частота дорівнює 5. Цій частоті відповідає значення ознаки 7.Отже, мода дорівнює 7.
Медіана вибірки
Розглянемо спочатку питання про впорядковану вибірку. Так називають вибірку , в якій усі її значення розташовані в порядку зростання або спадання. Розташуємо нашу вибірку в порядку зростання:
1,1,1,4,4, 4,4,5,6,7,7,7,7,7,8,8,9,9
Усього в ряду 18 членів (так як кількість учнів дорівнює 18)
А тепер пригадаємо, де в математиці ми зустрічались з терміном «медіана»?
Отже, медіана вибірки – це число, яке «поділяє» сукупність навпіл. В нашій задачі медіана дорівнює середньому арифметичному цих значень:
M= (6+7):2=6, 5
Отже, половина ( так як медіана «ділить» навпіл) учнів засвоїли предмет на 6,5 балів.
Алгоритм знаходження медіани вибірки ( Ml )
1. Упорядкувати сукупність ознак.
2. Якщо кількість членів ряду непарна, то медіаною є «середнє» число ряду.
3. Якщо кількість членів ряду парна, то медіана дорівнює середньому арифметичному двох «середніх» значень.
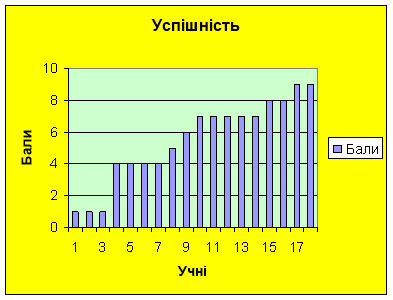
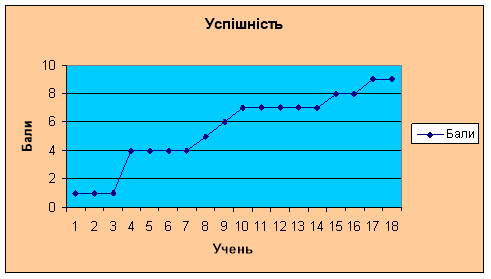
4. У статистиці стовпчасті діаграми називають гістограмами (гр.- стовп)
Для побудови гістограми, полігону відкладемо по горизонталі значення ознаки(кількість балів), а по вертикалі – частоти(кількість учнів, що їх одержали).
Алгоритм побудови стовпчастих діаграм ( гістограм), полігону
1. Відкласти по горизонталі ( вісь ОХ ) значення ознаки ( кількість балів).
2. Відкласти по вертикалі ( вісь ОУ ) частоти ( кількість учнів , що їх одержали).
3. У гістограмі кожний стовпчик закінчити горизонтальною лінією, в полігоні розподілу з’єднати відрізками середини верхніх основ послідовних прямокутників гістограми.
- Формування навичок та умінь
Учні працюють в експертних групах. Кожна група проводить статистичне дослідження на основі зібраних даних:
- складає частотну таблицю;
- обчислює відносну частоту найбільшого значення ознаки вибірки;
- знаходить центральні тенденції вибірки;
- будує гістограму, полігон.
Усі необхідні розрахунки учні виконують у робочих зошитах, на аркуші статистичного звіту фіксуються вже готові відповіді.
4.Закріплення нових знань
Після закінчення роботи в групах звіти здаються вчителю для остаточного оцінювання.
Кожна група обирає представника для захисту звіту.
Після перегляду звітів учителем вони вивішуються на дошку. По черзі заслуховується звіт кожної групи, учні повторюють основні поняття, виправляють помилки в звітах(якщо вони є).
Після захисту звітів слухається повідомлення про завдання математичної статистики та сфери її застосування
(додаток 3).
6. Домашнє завдання.
За підручником Г.П.Бевз «Алгебра і початки аналізу» 10 -11 кл.(2005) вивчити параграф 48, розв’язати № 869, стр.201.
7. Підведення підсумків уроку.
Вчитель пропонує учням виділити основні положення вивченого матеріалу, оцінює діяльність учнів і дякує їм за співпрацю.
Додаток 1
Картка - інструкція
Алгоритм - скінчена послідовність дій, направлених на досягнення мети або на розв’язання поставленого завдання.
Алгоритм знаходження середнього значення вибірки ( х )
1. Знайти добутки значень вибірки на їх частоту.
- Скласти всі добутки ( одержимо суму всіх значень вибірки).
- Одержану суму поділити на загальну кількість членів вибірки.
Алгоритм знаходження моди вибірки ( Мo)
- Знайти в рядку частот найбільше число (їх може бути декілька найбільших і рівних між собою).
- У рядку значень ознаки знайти відповідні значення, які відповідають найбільшій частоті або частотам.
Алгоритм знаходження медіани вибірки ( Ml )
- Упорядкувати сукупність ознак.
- Якщо кількість членів ряду непарна, то медіаною є «середнє» число ряду.
- Якщо кількість членів ряду парна, то медіана дорівнює середньому арифметичному двох «середніх» значень.
Алгоритм побудови стовпчастих діаграм ( гістограм) , полігону
- Відкласти по горизонталі ( вісь ОХ ) значення ознаки ( кількість балів).
- Відкласти по вертикалі ( вісь ОУ ) частоти ( кількість учнів , що їх одержали).
- У гістограмі кожний стовпчик закінчити горизонтальною лінією, в полігоні розподілу з’єднати відрізками середини верхніх основ послідовних прямокутників гістограми.
Опорний конспект
Перші відомості про статистику
![]() Математична статистика Розділ прикладної математики в якому досліджуються характеристики масових явищ
Математична статистика Розділ прикладної математики в якому досліджуються характеристики масових явищ
Стовпчасті діаграми Гістограми
Вибірка опитують вибірково всього кілька десятків чи сотень людей
Частоти показують як часто зустрічаються у вибірці ті чи інші значення
Відносна частота вибірки відношення частоти до числа усіх значень вибірки
Центральні тенденції
Середнє значення вибірки середнє арифметичне усіх її значень
Мода вибірки те її значення яке трапляється найчастіше
Медіана вибірки число яке «поділяє» навпіл упорядковану сукупність значень вибірки
Додаток 2
Повідомлення «З історії розвитку статистики»
Статистика - наука, що збирає, обробляє і вивчає різні дані, пов’язані з масовими явищам, процесами і подіями. Предметом вивчення статистики є, зокрема, кількісний склад масових суспільних явищ і процесів у зв’язку з їхнім якісним.
Іноді неточно визначають статистику як «науку збирання даних». Це галузь прикладної математики.
Математична статистика – розділ математики, присвячений математичним методам систематизації, обробки й використання статистичних даних для наукових і практичних висновків.
Статистика виникла з практичних потреб людей , їх господарської діяльності, необхідності обліку земельних угідь, майна, кількості населення вивчення його занять, вікового складу … Цікаво, що в Англії в 17 ст. , коли статистичне вивчення поширилось на явища суспільного життя, людей, що займались цими питаннями , називали «політичними арифметиками». Одним із головних представників «політичних арифметиків» Англії був В.Петті (1625-1687).
Додаток 3
Повідомлення «Завдання математичної статистики».
Завдання математичної статистики полягає в тому , щоб на основі властивостей деякої вибірки елементів, узятих з генеральної ( усієї ) сукупності , зробити певні висновки про властивості всієї генеральної сукупності.
У зв’язку з розвитком підприємства, коли товари виготовляються великими партіями , постає дуже важливе завдання: визначити якість усієї партії продукції, дослідивши невелику вибірку з неї.
Звичайно, перевірка всієї партії займе дуже багато часу, крім того, іноді просто неможливо перевірити всю партію. Наприклад, як
перевірити всю партію виготовленого фотопаперу? Адже після перевірки він весь стане зіпсованим.
Аналогічні приклади можна навести з перевіркою міцності тканини на розрив, якості електричних ламп та ін.
Методи математичної статистики приносять велику економію, вони поширено використовуються в економіці і називаються статистичними методами контролю.
Статистичні методи також використовуються в теорії надійності, яка дає змогу визначити ймовірність передчасного виходу з ладу певних виробів, наприклад телевізорів.
Методи математичної статистики застосовують в усіх галузях науки і техніки, в соціології, політології, економіці та різних сферах бізнесу.
Додаток 4
Лист статистичного звіту учнів _______ групи 1
Керівник групи __________
Члени групи ______________________________
Завдання _________________________________
Вид статистичного спостереження :
За часовою ознакою
За способом організації
За ступенем охоплення одиниць
Частотна таблиця
Ознака
Частота
Відносна частота найбільшого значення вибірки :
Середнє значення вибірки
Мода вибірки:
Медіана вибірки:
Побудувати гістограму, полігон
Лабораторно-практична робота з інформатики
Тема: «Складання алгоритмів»
Мета: Навчитись складати алгоритми до розв’язування прикладних задач;
визначати основні етапи розв’язування задач;
навчитись складати математичну модель задачі.
Матеріально – технічне забезпечення: IBM PC
Теоретичні відомості
Алгоритм –це насамперед задане зрозуміле і точне розпорядження щодо виконання певної послідовності дій для отримання розв’язку задачі за визначене число кроків.
Математична модель –математичний опис якого – небудь процесу.
Розв’язування задач за допомогою комп’ютера включає основні етапи, частина яких здійснюється без застосування комп’ютера.
Основні етапи розв’язання прикладних задач .
- Постановка задачі:
- збір інформації про задачу;
- формулювання умови задачі;
- визначення кінцевої мети розв’язування задачі.
2. Аналіз і дослідження задачі:
- аналіз технічних і програмних засобів;
- розробка математичної моделі.
3. Розробка алгоритму:
- вибір форми запису алгоритму( блок – схеми)
- проектування алгоритму.
4.Використати можливості програми Excel для розв’язування задачі.
Порядок виконання роботи
1.По заданому завданню скласти необхідного виду алгоритм, використовуючи математичне моделювання.
2. Ввімкнути комп’ютер і запустити програму Excel.
3. Визначити центральні тенденції вибірки та побудувати за допомогою даної програми діаграми( гістограму та полігон).
4.Проаналізувати результати розв’язання задачі, зробити уточнення в разі потреби математичної моделі.
Дати відповіді на питання:
- Який тип базової алгоритмічної конструкції Ви використали при розв’язуванні задачі?
- Чи надає програма Excel переваги в обчисленні центральних тенденцій та в побудові діаграм над традиційними способами будувати та обчислювати їх вручну ? Відповідь поясніть.
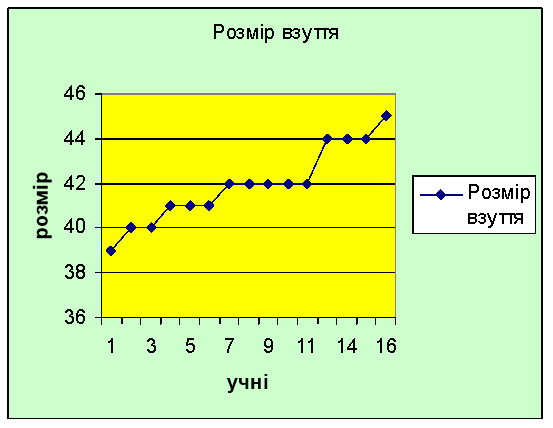
Завдання 1. Визначення розміру взуття юнаків в гр.№13 ВШ-07
|
№ учня |
Розмір взуття |
|
1 |
39 |
|
2 |
40 |
|
3 |
40 |
|
4 |
41 |
|
5 |
41 |
|
6 |
41 |
|
7 |
42 |
|
8 |
42 |
|
9 |
42 |
|
10 |
42 |
|
11 |
42 |
|
13 |
44 |
|
14 |
44 |
|
15 |
44 |
|
16 |
45 |
|
Середнє значення |
41,93333333 |
|
Мода |
42 |
|
Медіана |
42 |

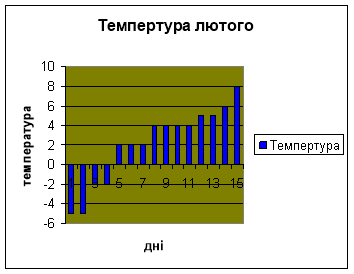
Завдання 2. Визначення розміру температури за лютий.
|
День |
Темпертура |
|
1 |
-5 |
|
2 |
-5 |
|
3 |
-2 |
|
4 |
-2 |
|
5 |
2 |
|
6 |
2 |
|
7 |
2 |
|
8 |
4 |
|
9 |
4 |
|
10 |
4 |
|
11 |
4 |
|
12 |
5 |
|
13 |
5 |
|
14 |
6 |
|
15 |
8 |
|
Середнє значення |
2,133333333 |
|
Мода |
4 |
|
Медіана |
4 |
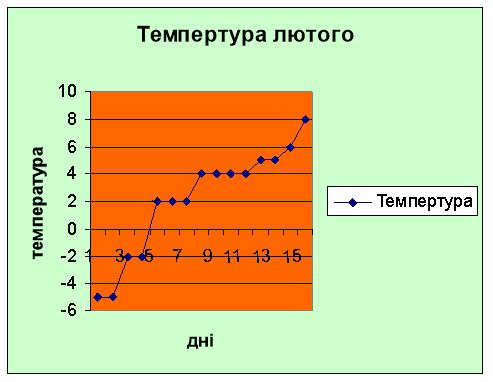
Завдання 3.Визначення зросту юнаків в гр.№13 ВШ-07
|
№ учня |
Зріст учня, см |
|
1 |
165 |
|
2 |
169 |
|
3 |
169 |
|
4 |
170 |
|
5 |
171 |
|
6 |
171 |
|
8 |
175 |
|
9 |
175 |
|
10 |
176 |
|
11 |
177 |
|
12 |
179 |
|
13 |
179 |
|
14 |
180 |
|
15 |
185 |
|
16 |
185 |
|
Середнє значення |
175,0666667 |
|
Мода |
169 |
|
Медіана |
175 |
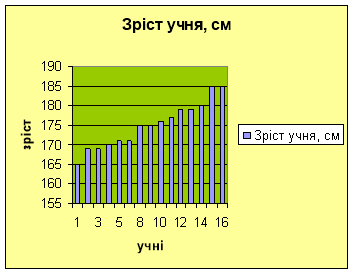
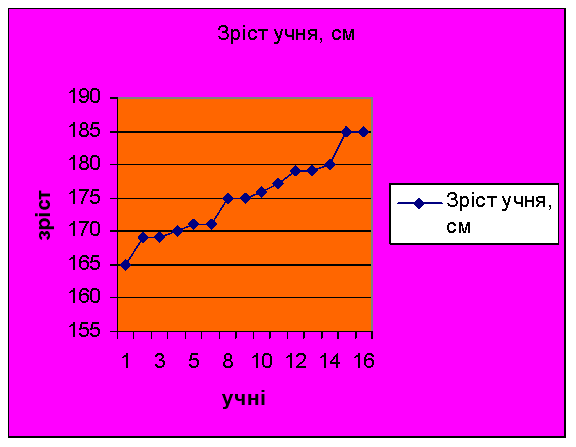
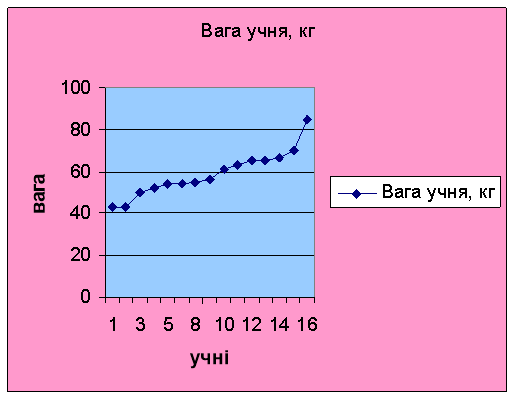
Завдання 4. Визначення ваги юнаків в гр.№13 ВШ-07
|
№ учня |
Вага учня, кг |
|
1 |
43 |
|
2 |
43 |
|
3 |
50 |
|
4 |
52 |
|
5 |
54 |
|
6 |
54 |
|
8 |
55 |
|
9 |
56 |
|
10 |
61 |
|
11 |
63 |
|
12 |
65 |
|
13 |
65 |
|
14 |
67 |
|
15 |
70 |
|
16 |
85 |
|
Середнє значення |
58,86666667 |
|
Мода |
43 |
|
Медіана |
56 |
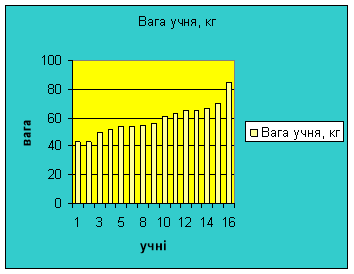


про публікацію авторської розробки
Додати розробку
