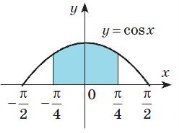
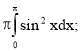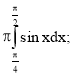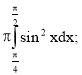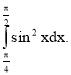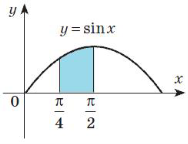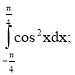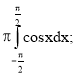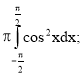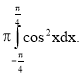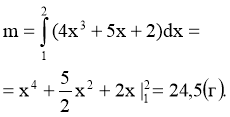Застосування визначеного інтеграла в фізиці, техніці, економіці
Урок проведено в 11-му класі. Математика. Алгебра. (рівень стандарту). Мета уроку: Продовжити формування навичок знаходити визначений інтеграл, показати його місце і значення в розв'язуванні задач фізичного змісту.
Сформувати уявлення про застосування визначеного інтеграла до розв'язування прикладних задач.
Розглянути приклади застосування визначеного інтеграла до розв'язування прикладних задач: знаходження переміщення точки за поданий проміжок часу; обчислення роботи, яку треба виконати для переміщення тіла із однієї точки в другу; обчислення маси неоднорідного стержня, якщо відомо, як змінюється його лінійна густина; обчислення величини заряду, що переноситься за певний проміжок через переріз провідника.
Працювати над формуванням умінь учнів застосовувати визначений інтеграл до розв'язування прикладних задач.
Розвивати вміння узагальнювати, реалізувати практичні зв'язки курсів математики та фізики, формувати пізнавальний досвід учня.
Виховувати культуру розумової праці, інтерес до математики, інтерес до науки, бачення цілісності світу. Формування розуміння місця та ролі математики в сучасному світі.
Конспект уроку опублікований в каталозі файлів на Сайті вчителя математики ВАЛЕНТИНИ ВОЛОШИНОЇ: http://volochinaviv1.ucoz.ru
Спеціалізована школа № 7 ім. М. Т. Рильського
м. Києва
Застосування визначеного інтеграла в фізиці, техніці, економіці
Алгебра та початки аналізу 11 клас
Рівень стандарту

Волошина Валентина Іванівна
вчитель математики
вчитель вищої категорії
вчитель - методист
Київ 2018
Тема уроку: Застосування визначеного інтеграла в фізиці, техніці, економіці
Мета уроку:
Продовжити формування навичок знаходити визначений інтеграл, показати його місце і значення в розв’язуванні задач фізичного змісту.
Сформувати уявлення про застосування визначеного інтеграла до розв’язування прикладних задач.
Розглянути приклади застосування визначеного інтеграла до розв’язування прикладних задач: знаходження переміщення точки за поданий проміжок часу; обчислення роботи, яку треба виконати для переміщення тіла із однієї точки в другу; обчислення маси неоднорідного стержня, якщо відомо, як змінюється його лінійна густина; обчислення величини заряду, що переноситься за певний проміжок через переріз провідника.
Працювати над формуванням умінь учнів застосовувати визначений інтеграл до розв’язування прикладних задач.
Розвивати вміння узагальнювати, реалізувати практичні зв’язки курсів математики та фізики, формувати пізнавальний досвід учня.
Виховувати культуру розумової праці, інтерес до математики, інтерес до науки, бачення цілісності світу. Формування розуміння місця та ролі математики в сучасному світі.
Обладнання: Презентація PowerPoint - інтерактивний супровід уроку. Вислів: «Природа формує свої закони мовою математики. Галілео Галілей». Картки тестових завдань, робочі зошити.
Хід уроку:
І. Мотивація навчальної діяльності
Організаційні питання, щодо початку уроку. Вчитель повідомляє тему уроку, роздає картки тестових завдань, викликає до дошки учнів для перевірки домашнього завдання. В зошитах записують дату уроку та тему.
Вчитель: Вам відомі деякі приклади застосування визначеного інтеграла до розв’язування геометричних задач, зокрема обчислення площ і об’ємів тіл. У цих випадках величини, які знаходять, можна розглядати як функції відрізка. Сьогодні спробуємо за допомогою математики розв’язати проблеми, що виникають на уроці фізики.
ІІ. Перевірка домашньої роботи.
Перевірка домашнього завдання проводиться по варіантам (завдання подібні до домашнього), з елементами обговорення правильності виконаних обчислень, повторенням означення визначеного інтеграла, таблиці первісних елементарних функцій, правил обчислення первісних. Учні перевіряють виконання домашнього завдання, виправляють помилки.
Варіант 1
- Укажіть формулу, за допомогою якої можна обчислити об’єм V тіла, утвореного під час обертання навколо осі Ох криволінійної трапеції, зображеної на рисунку.
|
А)
В) |
|
-
Обчисліть об’єм тіла, утвореного обертанням навколо осі криволінійної трапеції, обмеженої лініями
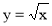 ,
, 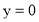 ,
, 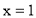 ,
, 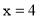 .
.
А) 1,5π; Б) 7,5 π; В) 7,5; Г) 5π.
-
Обчисліть об’єм тіла, утвореного обертанням навколо осі Ох фігури, обмеженої лініями
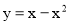 і
і 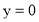 .
.
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
Варіант 2
- Укажіть формулу, за допомогою якої можна обчислити об’єм V тіла, утвореного під час обертання навколо осі Ох криволінійної трапеції, зображеної на рисунку.
|
А)
В) |
|
-
Обчисліть об’єм тіла, утвореного обертанням навколо осі криволінійної трапеції, обмеженої лініями
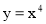 ,
, 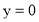 ,
, 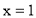 ,
, 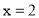 .
.
А) 6,2; Б) 6,5 π; В) 6,2 π; Г) 5,8π.
-
Обчисліть об’єм тіла, утвореного обертанням навколо осі Ох фігури, обмеженої лініями
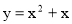 і
і  .
.
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
ІІІ. Актуалізація опорних знань.
Існують фізичні величини, які також можна розглядати як функції відрізка. Наприклад, переміщення обчислюють залежно від відрізка часу руху, робота сили під час руху тіла по прямій залежить від пройденого відрізка шляху, електричний заряд, що проходить через поперечний переріз провідника, залежить від відрізка часу, за який проводять вимірювання тощо. Ці та інші величини можна обчислити за допомогою визначеного інтеграла. Отже, завдання уроку – розглянути приклади застосування визначеного інтеграла до обчислення величин. Тому корисно повторити Деякі відповідності між формулами і фізичними величинами.
Математичне лото:
Встановити відповідність між формулою і фізичними величинами, які вона пов’язує.
|
|
А. Робота і потужність Б. Сила струму і електричний заряд В. Швидкість руху і переміщення Г. Лінійна густина і маса стрижня |
IV. Засвоєння нових знань.
Фізика вивчає різні явища і процеси, які пов’язані зі змінними величинами, обчислювати які значно легше за допомогою визначеного інтеграла. З’ясуємо, як саме ми можемо застосувати визначений інтеграл у фізиці.
Застосування визначеного інтеграла до розв’язування прикладних задач.
(Доповіді окремих учнів, які по черзі доповідають свою задачу, конспективно записують матеріал на дошці і в робочих зошитах)
- Знаходження переміщення точки за поданий проміжок часу.
Припустимо, що точка рухається по прямій (по осі Ox ) і відома швидкість цієї точки. Знайдемо переміщення s точки за проміжок часу [t1;t2]. Розглянемо відрізок часу [t; t+Δt] і будемо вважати швидкість на цьому відрізку сталою. Тоді одержимо: Δs(t)=v(t)Δt, звідки
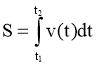 . (1)
. (1)
- Обчислення величини заряду, що переноситься за певний
проміжок часу через переріз провідника.
Обчислимо величину q заряду, що переноситься за проміжок часу [t1 ; t2] через переріз провідника. Нехай задано закон зміни струму I = I(t) залежно від часу. Тоді на малому проміжку часу [t;t + Δt] можна вважати силу струму сталою, яка дорівнює I(t), а Δq = I(t)Δt . Отже,
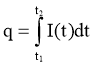 . (2)
. (2)
- Обчислення роботи, яку треба виконати для переміщення тіла із однієї точки в другу.
Нехай тіло рухається по осі Ox, у кожній точці якої прикладено деяку силу F = F(x). Обчислимо роботу A, яку необхідно виконати під час переміщення із точки x1 у точку x2 . На малому відрізку шляху від точки x до точки x + Δx можна вважати силу сталою, яка дорівнює F(x). Тоді ΔA(x) = F(x)Δx. Звідси одержуємо, що всю роботу на відрізку [x1;х2] можна записати у вигляді інтеграла:
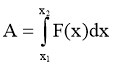 . (3)
. (3)
- Обчислення кількості теплоти
Q – кількість теплоти, с – теплоємність
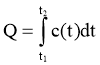 . (4)
. (4)
- Обчислення маси неоднорідного стержня.
Обчислимо масу m неоднорідного стержня, якщо відомо, як змінюється його густина ρ(x). Розглянемо відрізок [x;x + Δx]. Вважаючи, що на цьому відрізку густина стала, маємо: Δm(x) = ρ(x)Δx , звідси:
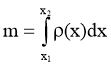 . (5)
. (5)
- Економічний зміст інтеграла.
Якщо f(t) – продуктивність праці в момент часу t, то обсяг виробленої продукції за проміжок [0;Т] можна обчислити за формулою:
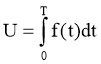 . (6)
. (6)
V. Удосконалення вмінь і навичок
Демонстрація таблиці
|
|
|
Величини |
Знаходження похідної |
Знаходження інтеграла |
|
1 |
Переміщення |
s – переміщення v– швидкість |
|
|
|
2 |
Заряд |
q – електричний струм I – сила струму |
|
|
|
3 |
Робота за прямолінійного руху |
А – робота F – сила |
|
|
|
4 |
Кількість теплоти |
Q – кількість теплоти с – теплоємність |
|
|
|
5 |
Маса |
m – маса
|
|
|
Розв’язування задач
Задача 1. Для кращого обслуговування заїзду гонок серії «Формула-1» майстри визначили найкращий закон зміни швидкості руху автомобіля прямою трасою:
![]() . Який шлях:
. Який шлях:
а) проїде пілот цієї гонки за 7 с. від початку руху;
б) він проїде за сьому секунду?
Розв’язання: Знаходимо шлях за формулою 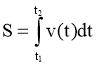
а) 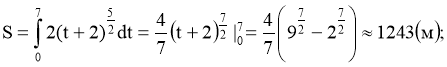
б) 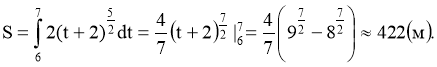
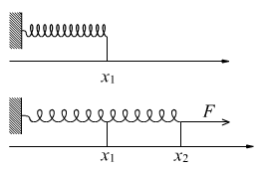
Задача 2. Яку потрібно виконати роботу, щоб розтягнути пружину на 3 см, якщо сила в 10 Н розтягує пружину на 1 см?
Розв’язання: Згідно з законом Гука, сила F, що розтягує пружину, пропорційна переміщенню х вільного кінця пружини, тобто F=kx.
|
Для знаходження коефіцієнта k скористаємось тим, що сила в 10Н розтягує пружину на 0,01 м: 10=0,01∙ k,
k=1000. Тоді F=1000х і роботу знаходимо за формулою |
|
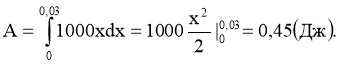
Задача 3. Обчисліть масу ділянки стрижня від х1=1 до х2=2, якщо його лінійна щільність задається формулою ρ(х)=4х3+5х+2 (г/см).
Розв’язання: Знаходимо масу ділянки за формулою 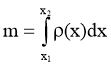 .
.
|
|
|
Задача 4. Протягом 7 с. величина струму в провіднику змінювалась за законом I(t)=3t2+2t (А). Знайдіть кількість електрики, що пройшла через провідник за цей час.
Розв’язання: За формулою 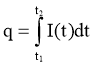 маємо
маємо
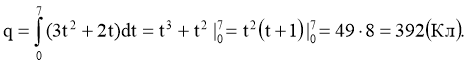
Задача 5. Продуктивність праці робітничої бригади визначається в залежності від часу t функцією f(t)=4t3+1. Знайдемо обсяг продукції за другу і третю годину робочого дня.
Розв’язання: За формулою 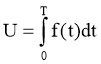 дістаємо:
дістаємо:
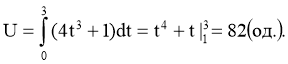
Робота в парах
Учні працюють над задачами й звіряють відповіді із відповідями, заздалегідь підготовленими вчителем на дошці.
1. Яку роботу треба виконати для стискання пружини на 4 см, якщо відомо, що сила 2Н стискає цю пружину на 1 см?
2. Обчисліть величину заряду, що переноситься через поперечний переріз провідника за 20 с, якщо сила струму змінюється за законом I(t) = 2t +1 (А).
3. Швидкість руху тіла в момент часу t (с) задано формулою v = 15 − 3t (м/с). Який шлях подолає тіло від початку руху до повної зупинки?
4. Знайдіть масу неоднорідного стержня завдовжки 40 см, якщо його лінійна густина змінюється за законом ρ(l)=2l2+1 (кг/м).
Додаткові вправи:
1. Обчислити роботу, виконану при викачуванні води з резервуара циліндричної форми (R=2м, H=1м), вщент наповненого водою (вага води об’ємом 1м3 наближено дорівнює 9807Н).
2. Тіло масою 2 кг рухається прямолінійно під дією сили F(t) = 12t − 8(Н). Знайдіть закон його руху, якщо в момент часу t = 3 с. швидкість тіла дорівнює 10м/с, а координата 21м.
VІ. Підсумок уроку
На уроці ми дізналися, що поняття інтегралу з'явилося в результаті практичної діяльності людини, використовується сьогодні в самих різних сферах науково-практичної діяльності людини, а саме: фізиці, хімії, біології, механіці, економіці, філології і т.д.
Наведіть приклади застосування визначеного інтеграла до розв’язування прикладних задач. Перелічіть відомі вам типи задач з фізики й техніки, які були розв’язані за допомогою інтеграла на уроці.
Раніш ми розв’язували фізичні задачі за допомогою похідної. Знаємо задачі, що приводять до поняття визначеного інтеграла. Інтеграл – це ключ , який відчиняє ворота між фізикою та математикою. Тут вони поєднуються в одне ціле.
Додатково: Підчас підведення підсумку уроку, можна розв’язати кросворд. (Кросворд створено за допомогою ресурсу:
http://biouroki.ru/workshop/crossgen.html )
|
|
|
|
|
|
3 |
|
9 |
|
4 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
6 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
9 |
|
4 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
6 |
|
2 |
|
і |
|
л |
|
к |
|
|
н |
|
|
|
|
|
|
|
|
|
1 |
п |
і |
д |
і |
н |
т |
е |
г |
р |
а |
л |
ь |
н |
а |
|
|
|
|
|
|
|
|
е |
|
и |
|
т |
|
б |
|
и |
|
|
ю |
|
|
|
|
|
|
|
|
|
|
р |
|
ф |
|
е |
|
н |
|
в |
|
|
т |
|
|
|
|
|
|
|
|
|
|
в |
|
е |
|
г |
|
і |
|
о |
|
|
о |
|
|
|
|
|
|
|
|
|
|
і |
|
р |
|
р |
|
ц |
|
л |
|
|
н |
|
|
|
|
|
|
|
|
|
|
с |
|
е |
|
а |
|
|
|
і |
|
|
|
|
|
|
|
|
|
|
|
|
|
н |
|
н |
|
л |
|
|
|
н |
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
ц |
|
|
|
|
8 |
і |
н |
т |
е |
г |
р |
у |
в |
а |
н |
н |
я |
|
|
|
|
і |
|
|
|
|
|
й |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
7 |
ф |
у |
н |
к |
ц |
і |
я |
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
Запитання до кросворда.
- Як називається функція, яка стоїть під знаком інтеграла? (підінтегральна)
- Як називається множник dx у підінтегральному виразі? (диференціал)
-
Що позначає символ
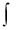 , який з’явився наприкінці ХVII століття і утворився із скорочення латинського слова Summa: S? (інтеграл)
, який з’явився наприкінці ХVII століття і утворився із скорочення латинського слова Summa: S? (інтеграл)
- Як називається трапеція, площу якої ми знаходимо за допомогою визначеного інтеграла? (криволінійна)
- Хто з відомих математиків-фізиків дослідив фізичний зміст інтеграла? (Ньютон)
- Як називається функція F(x) для функції f(x), якщо її похідна F'(x) дорівнює f(x)? (первісна)
- Як називається правило (залежність), яке кожному елементу з першої множини ставить у відповідність один і тільки один елемент з другої множини? (функція)
- Як називається операція обернена до операції диференціювання? (інтегрування)
- Хто з відомих математиків дослідив геометричний зміст інтеграла? (Лейбніц)
Домашнє завдання.
Задача 1. Резервуар конічної форми з вершиною, зверненою донизу, наповнений водою. Яку роботу потрібно виконати, щоб викачати з нього всю воду, якщо радіус основи конуса R=50см, а висота Н=1 м.
Задача 2. Два одиничні електричні заряди розташовані на відстані 5 см один від одного. Потім один із зарядів звільняється і віддаляється від іншого під дією сили відштовхування, яка, за законом Кулона, має вигляд ![]() , де k – коефіцієнт пропорційності. Яку роботу здійснить сила, якщо заряд віддалиться на відстань:
, де k – коефіцієнт пропорційності. Яку роботу здійснить сила, якщо заряд віддалиться на відстань:
1) 10 см; 2) 15 см?
Використаний ресурс:
- https://www.schoollife.org.ua/1271-2016/
- http://slavmmc.at.ua/matematika/Integrovanij.doc
- http://svitppt.com.ua/matematika/rozvyazuvannya-prikladnih-zadach-za-dopomogoyu-viznachenogo-integrala.html
- http://shkola.ostriv.in.ua/publication/code-50409747F5617/list-B65BB05F26
- http://osvita.ua/school/lessons_summary/math/38847/
- http://metodportal.com/node/8968


про публікацію авторської розробки
Додати розробку