Матеріал до уроку "Професійна спрямованість у викладанні математики"

Зеленодольський професійний ліцей

 

Професійна

спрямованість

у викладанні

математики

Збірник задач

практичного змісту

 

 

 

Підготувала:       Дашко І.М.

 

Зеленодольськ

2018 рік

 

Методична розробка

 

завдань професійної спрямованості з

математики

 

Зміст:

1.Задачі професійного змісту для різних   

   спеціальностей.

2.Задачі, що демонструють міжпредметні зв'язки.

3.Задачі практичного змісту з різних тем геометрії.

4.Історичні задачі.

 

 

 

 

 

 

Підготувала:         викладач Дашко І.М.

Анотація

до методичної  розробки

«Професійна спрямованість у викладанні математики»

В даній методичній розробці запропоновані задачі професійної спрямованості і практичного змісту для різних робітничих спеціальностей, як то кухарів, електромонтерів, будівельників.

Наведені приклади задач, що демонструють міжпредметні зв’язки (математики з кресленням, фізикою, екологією та іншими предметами).

Одним з основних напрямків реформи професійно – технічної освіти є необхідність більш тісно пов᾽язувати викладання загальноосвітніх предметів, в тому числі і математики, з отримуваною професією. Нормою сьогодення є потреба в оволодінні  щонайменш двома, а то і декількома професіями, адже,такі умови диктує ринок праці. А, отже, щоб бути конкурентоспроможним на ньому, майбутньому робітникові треба постійно вчитися, набувати нові знання, оволодівати новітніми технологіями.

Вважаю, що саме професійна спрямованість у викладанні математики допоможе учням краще оволодіти знаннями, пов᾽язати їх з майбутньою професією, впевнено почуватися серед великої кількості технічних нововведень.

 

 

Задачі  професійної  спрямованості

( для спеціальності електромонтер ) .

 

Термосифонний фільтр являє

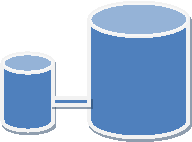собою вертикально розміщений          

циліндр, приєднаний з допомогою

трубок до   бака трансформатора.

Знайти діаметр дна  і висоту

фільтра,якщо його бічна

поверхня S , а об'єм   V.

 

 

Кабельний колектор прямо-

кутного  перерізу має розміри

2300х2400х30000мм².

Знайти площу поверхні колектора

 

 

 

Циліндрична стальна шайба для

редуктора-вентилятора

тепловоза має такі розміри :

зовнішній діаметр 8см,

внутрішній діаметр 1.2см ,

висота шайби 7.5см.

Визначити об'єм шайби.

Задачі  професійної  спрямованості

( для спеціальності електромонтер ) .

 

 

•                   Кабель складається  з

чотирьох  жил , кожна з

яких  має  діаметр 4мм.

Знайти діаметр кабелю,

якщо товщина ізоляції 1 мм.

Визначити площу поверхні

відрізка кабелю довжиною 1м.

 

 

 

•                                                                                                              Скільки мідного дроту діаметром 5 мм можна прокатати із злитка об'ємом 0,5 м³ ?

 

 

Задачі професійної спрямованості

( для спеціальності будівельник).

 

Залізобетонна панель має розмір 600X120X22 см, По всій довжині - 6 циліндричних отворів, діаметр яких 14см, Знайдіть масу панелі, якщо густина матеріалу 2,5т/м³.

 

 

 

 

 

Кусок металу массою 69 гр. має об'єм на 10 см³ меньше другого куска металу массою    110гр Визначити      густину      обох      кусків      металу

знаючи, що   густина   першого   на  0,4 гр  /см³ більше, ніж другого.

 

 

 

 

 

 

Задачі професійної спрямованості

( для спеціальності будівельник) .

 

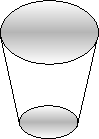
Скільки фарби потрібно для фарбування зовнішній поверхні 100 відер у вигляді конусу, якщо діаметр відер 25 см і ЗО см, яка становить 27,5 см і якщо на 1 м² потрібно 150 г оліфи.

 

 

 

 

 

 

 

Скільки    покрівельного    заліза    потрібно    для

покриття даху вежі, яка має форму шестикутної

правильної піраміди зі стороною основи  1,2 м, якщо грані нахилені до площини основи під кутом

60⁰

 

 

 

Задачі професійної спрямованості

(для спеціальності будівельник).

 

 

При нагріванні тіла розширюються. Тіла збільшують свою первісну довжину. Коефіцієнти лінійного розширення відповідно рівні: цегли -0,000005, скла - 0,00001, фарфору - 0,000008, цементу -0,000014, Записати коефіцієнти як степінь.

 

 

 

 

 

 

Стальний канат діаметром 20 мм накручений в один шар на барабан під'ємноі машини діаметром

в   2,5   м.   Скількі   витків   треба   накрутити   на

барабан,   щоб   кінець   каната  досягнув   глибини

шахти в  400м.

 

 

Міжпредметні   зв’язки.

Зв’язок   математики  зі

спецтехнологією кухарів

 

 

 

Задача №1

 

  Визначити місткість каструлі висотою

40см і діаметром основи 35см.

 

 

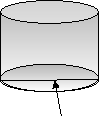
       V = S_осн ∙ h                  h=40cм

                       d=35см

 

                    

Міжпредметні   зв’язки.

Зв’язок   математики  зі

спецтехнологією кухарів

 

Задача №2

 

   Ціна одного кілограма цукерок знизилася

   на 2,4 гривень, що складає 15% ціни.      

   Скільки коштував кілограм цукерок до  

   зниження?

Задача №3

 

За 5кг крупи і 4кг борошна  за  платили 60гривень. Скільки коштує 1кг борошна і 1кг крупи якщо, 3кг крупи дорожчі за 2кг борошна на 14гривень.

 

                    

Міжпредметні  зв’язки.

Зв’язок   математики  зі

спецтехнологією кухарів

 

Задача №4

 

  Контейнер для овочів з (кришкою) має форму прямокутного паралелепіпеда. Сторони його основи відносяться як 1:2, а площа поверхні дорівнює 108см². Якими мають бути розміри контейнера, щоб його об’єм був найбільшим?

                                    V = a ∙ b ∙ h

 S = S_біч + 2 ∙ S_осн

                                                       S_осн = a ∙ b

    h

в

    а

                    

Міжпредметні  зв’язки.

Зв’язок   математики  зі

спецтехнологією кухарів

 

 

Задача №5

 

Креманка має форму півсфери діаметром 10см. Чи вмістить вона джем що зберігався в банці циліндричної форми висотою 10см і діаметром основи 7см ?

 D₁ D₂

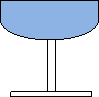 h

 

 

             V_ц = S_осн ∙h                        V = 4 ∙ π ∙ R₂²/6

            S_осн = π ∙ R₁²

 

Міжпредметні   зв’язки.

Зв’язок   математики  з  фізикою

 

 

 

 

 

Яку силу треба прикласти до вагона масою 8т так, щоб удержати його в рівновазі на рельсовому шляху, нахиленому  до обрію під кутом 0⁰28׳?

 

 

 

Знайдіть граничне навантаження, що може витримати латунний дріт, якщо діаметр його поперечного перерізу 2,5 мм, а граничне навантаження для латуні при розтягуванні становить 65 кг/мм².

 

Міжпредметні   зв’язки.

Зв’язок   математики  з  фізикою

 

 

Задача №3

 

 

 

Сталевий дріт діаметром 5 мм має межу міцності 85 кг/мм². При якій масі вантажу Q дріт може розірватися?

 

F

 

Задача №4

 

На кожен квадратний сантиметр площі поршня парової машини пара давить із силою 85 Н. Обчислите силу, з якої пара давить на весь поршень діаметром 420 мм.

 

 

 

 

Міжпредметні   зв’язки.

Зв’язок   математики  з  фізикою

 

 

Задача №5

 

Зовнішня окружність основи заводської труби має довжину 12,56 м, товщина труби 50см. Який тиск чинить труба на основу, якщо її маса 350 т?

Задача №6

 

Два прожектори розташовані один напроти іншого на прямолінійних паралельних протилежних берегах ріки. Відстань між прожекторами дорівнює 12 км. Прожектори можуть висвітлювати місцевість у радіусі 10 км кожний. Чому дорівнює площа поверхні ріки, освітлюваної цими прожекторами?

 

Міжпредметні   зв’язки.

Зв’язок   математики  з  кресленням.

 

 

 

Задача №1

 

 

             Для з'єднання двох дерев'яних брусів в одному з них випиляний фігурний паз ABCDE, в який вставляється відповідним чином випиляний кінець другого бруса

(мал. 1). Знайдіть CBA, якщо MАВ = 60°, a  BCD = 30°.

 

 

 

 

 

 

Міжпредметні   зв’язки.

Зв’язок   математики  з  кресленням.

 

 

 

Задача №2

 

 

На малюнку  показаний нераціональний (а) і раціональний (б) розкрій сталевої смуги при виготовленні заготівлі AFEDCB для деталей комбайна. Підрахуйте, скільки погонних метрів смуги буде зекономлено при виготовленні 200 заготівель (виміри на малюнку дані в міліметрах).

 

 

 

 

 

 

 

Міжпредметні   зв’язки.

Зв’язок   математики  з  кресленням

 

 

Задача №3

 

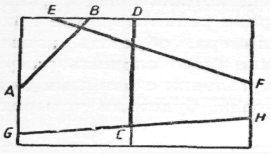
На малюнку  дані прямі АВ й CD, що перетинаються за межами аркуша в деякій точці М, і прямі EF й GH, що також перетинаються поза кресленням у деякій точці N. Як знайти довжину відрізка MN, кінцями якого служать точки М и N перетину даних прямих, а також середину цього відрізка?

 

 

 

  

        

Міжпредметні   зв’язки.

Зв’язок   математики  з  кресленням

 

 

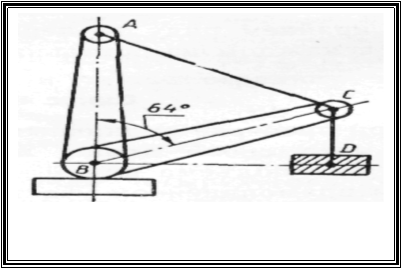
Задача №4

 

 

На малюнку  зображений навантажувальний кран, стріла ВС якого дорівнює 9м і може мати максимальне відхилення від вертикальної колони АВ на кут 64°. Знайдіть радіус дії крана (відстань від вантажу до вертикальної колони) .

 /

 

 

Міжпредметні   зв’язки.

Зв’язок   математики  з  кресленням

 

 

 

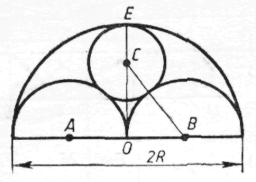
Задача №5

 

 

 

Підрахуйте радіус малого кола в конструкції рами вікна  зовнішня частина якої має вигляд півкола радіуса R.

 

 

 

 

 

 

 

 

Міжпредметні   зв’язки.

Зв’язок   математики  з  кресленням

 

 

 

Задача №5

 

 

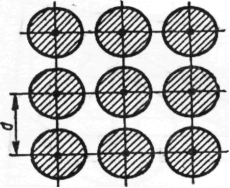
  У дощувальній установці розпилювачі розташовані по так званій квадратній схемі. При якій максимальній відстані d між розпилювачами установка буде зрошувати все поле, якщо один розпилювач зрошує коло радіуса r ?

 

 

 

Задачі практичного змісту по темі:

Паралельні  прямі.  Ознаки  паралельності  прямих

 

 

 

 

 

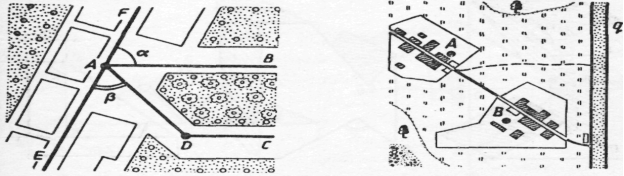
        На плані селища (мал. 1) вулиці АВ й DC паралельні, вулиці АВ й FE становлять кут α, а вулиці EF й AD— кут β . Знайдіть кути, які утворять вулиці AD й АВ, AD й DC.

 

 

 

 

 

 

 

 

Відповідь:

 

З малюнка 1 видно, що DAB= 180°- (α+ β ). Так як AB║DC, то BAD+ADC= 180°, звідки ADC= = l80° -BAD = α + β.

Задачі практичного змісту по темі:

Паралельні  прямі.  Ознаки  паралельності  прямих

 

 

 

      У місті 10 вулиць паралельні одна одній, а 10 інших вулиць перетинають їх під прямим кутом. Яке найменше число поворотів може мати замкнутий маршрут, що проходить через всі перехрестя?

 

 

 

 Відповідь:

 

        Легко привести приклад, коли поворотів 20. Доведемо, що менше 20 поворотів бути не може. Розглянемо 10 вулиць якого-небудь одного напрямку. Якщо маршрут проходить по всіх цих вулицях, то на кожній з них уже є не менш двох поворотів маршруту, і все доведено. Якщо ж найдеться така вулиця, по якій маршрут не проходить зовсім, то він повинен проходити по всім десятьох перпендикулярним вулицям. До них ми можемо застосувати те ж саме міркування.

Задачі практичного змісту по темі:

Паралельні  прямі.  Ознаки  паралельності  прямих

 

 

 

       По одну сторону шосе q перебувають два селища. Потрібно прокласти залізничну лінію l, паралельну шосе й таку, щоб сума відстаней від цих селищ до неї була найменшою. (Залізничну лінію й шосе прийняти за прямі, селища – за точки.)

 

 

 

 

 

 

 

 

 

 

Відповідь:

 

 

Проведемо пряму pq і спроектуємо точки А и В на пряму  p Буквами А₁ й В₁ позначимо проекції точок А і В на пряму р. Проведемо пряму l║q і відзначимо точку М перетину прямих l і р. Якщо М лежить між А₁ й В₁ то сума відстаней від точок А и В до  l дорівнює А₁ М + В₁М = А₁ В₁ (всі розглянуті довжини відрізків додатні). Якщо точка М лежить на продовженні відрізка А₁ В₁, то А₁М + В₁М > А₁ В₁ Таким чином, будь-яка пряма  l, паралельна прямій q, яка проходить між точками А и В, є шуканою  прямою.

 

 

 

 

 

 

 

Задачі практичного змісту по темі:

 

Задача №1

 

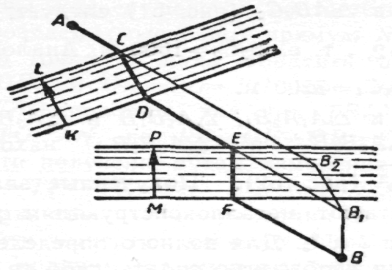
Між пунктами А и В протікає ріка (берега її приймаємо за паралельні прямі а й b). У якому місці ріки варто побудувати міст, щоб шлях від A до В був найкоротшим?  (Міст   перпендикулярний   берегу   ріки.) 

 

Рішення зображене на малюнку:

 

 

 

 

 

 

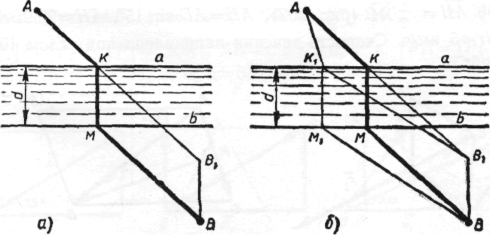
Задачі практичного змісту по темі:

Задача №2

        Населені пункти А и В розділені двома каналами, кожний з яких має паралельні береги. Де варто побудувати переправу через ці канали, щоб пункти А и В були з'єднані найкоротшими шляхом?

 

Відповідь:

 

Нехай MP й KL — відрізки, перпендикулярні відповідно лініям  берегів  каналів. Побудуйте образ точки В при паралельному перенесенні, що переводить М в Р, потім образ В при паралельному перенесенні, що переводить К в L. Шлях ACDEFB шуканий.

 

 

 

 

 

 

Задачі практичного змісту по темі:

 

Задача №3

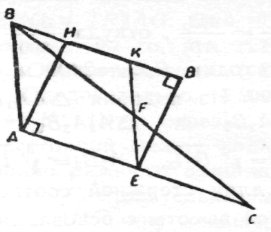
Заготовку, що має форму тупокутного ∆АВС, потрібно перекроїти в заготовку, що має форму прямокутника. Як це зробити?

 

Відповідь:

 

Проводимо EF— середню лінію ∆BAC, ∆FEC замінимо центрально-симетричним ∆FKB. Потім проводимо АНКВ й ∆АНВ паралельно переносимо в положення ∆EKQ.

 

 

 

 

 

 

 

З курсу математики французького автора Ж»

           Озанама (XVII в.).

 

«Троє хочуть купити будинок за 24 000 ліврів. Вони домовилися, що перший дасть половину, другий - одну третину, а третій - частину, що залишилася. Скільки дасть кожен?»

 

З «Загальної арифметики» Ньютона.

 

«Дехто бажає розподілити між бідняками гроші. Якби в нього було на вісім динарів більше, то він міг дати кожному по три, але він роздає лише по два й у нього залишається три. Скільки було бідняків?»

 

З «Арифметики» Л. Магницького.

 

«Один мандрівник іде з міста додому , а ходу його буде 17 днів, а інший мандрівник від дому до міста той же шлях творяше може пройти в 20 днів, обоє  ці чоловіки вирушили одночасно  від міст  своїх. Визначити, через скільки днів вони зустрінуться».

 

 

 

 

З «Арифметики» Л. Магницького

 

«Дехто прийшов у ряд, купив іграшок для малих хлопців: за першу іграшку заплатив ^1/5 частину всіх своїх грошей, за іншу ^3/7 остачі від першої покупки, за третю іграшку заплатив ^3/5 остачі від другої покупки; а по приїзду додому  у гаманці залишилось грошей 1 руб. 92 коп. Запитується, скільки в гаманці грошей було й скільки за яку іграшку грошей заплачено».

 

Із трактату «Математика в дев'ятьох книгах».

 

• «Спільно купують річ. Якщо кожна людина внесе по 8, то надлишок (дорівнює) 3. Якщо кожна людина внесе по 7, то недолік (дорівнює) 4. Запитується кількість людей і вартість речі».
• «Є 5 горобців й 6 ластівок, їх зважили на терезах. Вага всіх горобців важче ваги всіх ластівок. Якщо перемістити 1 ластівку й 1 горобця, то вага буде саме однаковою. Загальна вага ластівок і горобців 1 цзинь. Запитується, скільки важать ластівка  й горобець».

 

 

 

З «грецької антології».

 

«Ослиця й мул ішли разом, навантажені мішками рівної ваги. Ослиця скаржилася на вагу ноші. «Чого ти скаржишся, - сказав мул, - якщо ти мені даси один твій мішок, моя ноша стане вдвічі більше твоєї, а якщо я дам тобі один свій мішок, наші вантажі тільки зрівняються». Скільки було в кожного?»

 

З «Бахшалийского рукопису».

 

«Знайти число, яке від додавання 5 або віднімання 11 обертається в повний квадрат».

 

          З «Арифметики» Діофанта

 

• «Знайти три числа так, щоб суми всіх трьох і кожних двох були квадратами».

 

• «Знайти два числа, добуток яких, складений з кожним з даних чисел, складе куб деякого числа».

 

 

 

З «Книги абака» Л- Фибоначчи.

 

«Знайти число, 19/20 якого дорівнює квадрату самого числа».

 

      З «Арифметики» Магницкого.

 

«Знайти число, знаючи, що, склавши його квадрат з 108, виходить число, в 24 рази більше шуканого».

 

З «Загальної арифметики» Ньютона.

 

 

«Відомі периметр і площа прямокутного трикутника АВС. Знайти гіпотенузу ВС».

 

Задача Алькуина.

 

«Розділити сто мір пшениці між 100 особами так, щоб кожен чоловік одержав 3, кожна жінка 2, а кожне дитя ¹/₂ міри. Скільки чоловіків, жінок і дітей?»