Інтелектуальна гра «Найрозумніший». Алгебра 8 клас.
Мета : узагальнення знань учнів з алгебри за курс 8 класу; розвивати математичне й логічне мислення, кмітливість та індивідуальні здібності учнів виховання в учнів інтересу до математики, поглиблювати знання учнів з математики; закріпити знання про відомих вчених.
Обладнання: портрети математиків, вислови : «Математика – справа аж ніяк не тільки розуму, але також і фантазії...» ( Ф. Клейн); «Через рівняння, теореми
я всякі вирішував проблеми»( Джеффі Чосер); «Найдосконаліший мозок іржавіє без дії»( Шерлок Холмс), картки з завданнями.
Інтелектуальна гра «Найрозумніший»
Мета : узагальнення знань учнів з алгебри за курс 8 класу; розвивати математичне й логічне мислення, кмітливість та індивідуальні здібності учнів виховання в учнів інтересу до математики, поглиблювати знання учнів з математики; закріпити знання про відомих вчених.
Обладнання: портрети математиків, вислови : «Математика – справа аж ніяк не тільки розуму, але також і фантазії...»( Ф. Клейн); «Через рівняння, теореми
я всякі вирішував проблеми»( Джеффі Чосер); «Найдосконаліший
мозок іржавіє без дії»( Шерлок Холмс), картки з завданнями.
Хід заняття.
- Організаційна частина.
Вчитель: От і підійшли ми до завершення вивчення алгебри в 8 класі. І щоб зробити певні висновки про те, що ми знаємо, що ми вміємо, сьогодні ми проведемо урок у формі інтелектуальної гри «Найрозумніший».
Гра проходитиме в три тури:
Чи знаєш ти математиків
Моя улюблена категорія
А чи дружиш ти з задачами
І тур. А зараз приступаємо ми до першого туру «Чи знаєш ти математиків».
Вам було домашнє завдання повторити історичні довідки про математиків, які є у вашому підручнику.
Перед вами є прізвища 11 вчених: Платон, Пойа, Вієт , Гарріот, Діріхле ,Ролль, Діафант, Декарт, Ньютон, Лейбніц, Александрійський.
Вам буде подаватися якийсь факт з життя одного із них, вам треба відповісти - про кого, піднявши позначку з номером, що вказує на відповідного вченого, (перед учнями ставляться зображення цих вчених)
- З іменем якого із вчених пов'язана прямокутна система координат? (прямокутна Декартові система координат, тобто Рене Декарт)
- Хто із вчених запропонував операцію множення позначати однією крапкою, а операцію ділення - двома? (це був Готфрід Вільгельм Лейбніц)
- Хто це сказав: «Якщо ти хочеш навчитися плавати, то заходь у воду і пливи, а хочеш навчитися розв’язувати задачі, то розв’язуй їх»( Дьєрдь Пойа)
- Вони стали першими засновниками шкіл.(Платон , Арістотель)
- Хто із математиків став позначати невідомі величини голосними буквами А,Е,І,О…, а відомі – приголосними В,С,М,К,..?- (Франсуа Вієт)
- Хто з вчених визнав дроби рівноправними числами та сформулював поняття дробу ,як частки від ділення одного виразу на інший?(Ісаак Ньютон)
- Який математик увів знаки дій та нерівностей?
- Кому з вчених приписують сучасне означення функції? (Діріхле – Петер Густав Лежене)
- Хто перший використав сучасний знак радикала? (Мішель Роль)
- Теорему якого вченого ви вивчили по темі «Квадратні рівняння»
( Франсуа Вієт)
- Кому належить специфічний метод наближеного добування квадратного кореня? (Герон Александрійський)
- Хто перший використовував рівняння для розв’язування задач?( Діафант)
- Хто вперше увів термін «функція» (Гольтфрід Вільгельм Лейбніц)
Додаткові запитання для визначення 5 переможців.
Вибрати правильну відповідь на запитання
- При множенні степенів з однаковими основами степені:
А) віднімаються;
Б) перемножуються;
В) додаються;
Г) діляться.
2. Графіком оберненої пропорційності є:
А) пряма;
Б) гіпербола;
В) парабола;
Г) вітка параболи.
3. Яка множина уміщає в себе множину раціональних чисел ?
А) множина натуральних чисел;
Б) множина дійсних чисел;
В) множина цілих чисел;
Г) множина раціональних чисел.
4. Чому дорівнює ![]() ?
?
А) x3 ;
Б)- x3 ;
В) І x3І;
Г) x2 ;
5.Знайдіть середнє арифметичне коренів квадратного рівняння :
2![]() -3
-3![]()
А) ![]() ;
;
Б)![]() ;
;
В)![]()
Г) 3.
Відбір до ІІ туру.
Визначаємо в якому порядку будуть відповідати учасники гри. Для цього потрібно вибрати відповідні букви, щоб одержати слово.
- Графіком функції y=x2 є? (Парабола,67174587)
- Гілка гіперболи в одному напрямі наближається все ближче і ближче до осі ОХ, а в іншому напрямі - до осі ОУ. Відповідні прямі мають назву …
(Асимптота, 725863537)
ІІ Тур. А зараз ми переходимо до другого туру, який має назву «Моя улюблена категорія». Перед вами є 5 категорій знань з алгебри: Раціональні вирази, Квадратні корені, Квадратні рівняння, Функції, і категорія Сюрприз.
Дати якомога більше правильних відповідей за 1 хвилину.
Запитання до теми « Раціональні вирази».
1.Раціональні вирази поділяються на цілі і …(дробові)
2.Щоб поділити дріб на дріб …(перший помножити на дріб, обернений до другого).
3. При діленні степенів з однаковими основами показники…(Віднімають)
4. При піднесенні степеня показники …(Перемножують)
5.Основна властивість дробу…(Помножити чисельник і знаменник дробу на одне й те число)
6.Щоб піднести дріб до степеня,…(Піднести чисельник і знаменник)
7.А) х6∙х3∙х=…(х10);
Б)(х4)3=…(х12);
В)х8:х2=…(х6);
Г)х5∙х-2=…(х3);
8. А)![]() )0=…(1);
)0=…(1);
Б)![]() )0=…(1) ;
)0=…(1) ;
В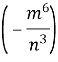 4=…(
4=…(![]() );
);
9.![]() =…(27);
=…(27);
10. 2-3=![]() );
);
11. 5-2=…![]() );
);
12.(-1)-259=… (-1)
13.![]() -2=…(4)
-2=…(4)
14. Чи записано число у стандартному вигляді?
А) 6,7∙10-4 (Так);
Б) 12,6∙104 (Ні ).
15. Знайти корені рівняння:
А) ![]() = 0 . (х=3);
= 0 . (х=3);
Б) ![]() =0 . (x=-3);
=0 . (x=-3);
В)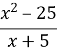 =0 . (x=5).
=0 . (x=5).
Запитання до теми «Квадратні корені».
1.Чи існує знак «квадратні корені»? (Ні)
2. Корінь з добутку дорівнює …(Добутку коренів)
3. Корінь з частки дорівнює…( Корінь з чисельника і знаменника)
4.Знайти квадратні корені з чисел: 100, 121, 0, 25, 81, 49.
5.Чи правильна рівність ?
А) ![]() =25. (Так)
=25. (Так)
Б) ![]() =-6. (Ні)
=-6. (Ні)
В) ![]() =0,2.(Ні)
=0,2.(Ні)
Г) ![]() =40.(Так)
=40.(Так)
6.Чи має зміст вираз?
А)![]() . (Так)
. (Так)
Б)![]() .(Ні)
.(Ні)
В)![]() . (Так)
. (Так)
Г) ![]() . (Так)
. (Так)
Д)![]() 2. (Ні)
2. (Ні)
7. Що більше ![]()
8.Обчислити:
А)![]() =…(3∙5=15)
=…(3∙5=15)
Б)![]() =…(10∙4∙7=280)
=…(10∙4∙7=280)
В)![]() =…(
=…(![]() =2,5)
=2,5)
9.Звільнитися від ірраціональності в знаменнику:
А)![]() =
=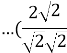 =
=![]() ;
;
Б)![]() =
=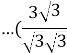 =
=![]() );
);
10. Обчислити:
А) (3-![]() )( 3+
)( 3+![]() )=… (7) ;
)=… (7) ;
Б) (5-![]() )( 5+
)( 5+![]() )=… (18).
)=… (18).
11. Скоротіть дріб :
А)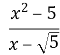 =…(x+
=…(x+![]() );
);
Б)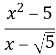 =…(x+
=…(x+![]() );
);
12.Обчислити:
А)7![]() +4
+4![]() - 5
- 5![]() =…(6
=…(6![]() );
);
Б) ![]() - 2
- 2![]() +3
+3![]() =…(2
=…(2![]() );
);
В) ![]() - 2
- 2![]() =…(3
=…(3![]() ).
).
Запитання до теми « Квадратні рівняння»
1.Квадратним рівнянням називають рівняння виду…(ax2+bx+c=0)
2.Рівняння, в якого b=0, називається…(Неповним квадратним)
3.Рівняння, в якого a=0 квадратним … (Не буде)
4.Якщо D=0, то рівняння має…(Два рівних корені,х=![]() )
)
5. Якщо D![]()
6.D=…(b2-4ac).
7. D![]()
8.Яке з даних рівнянь квадратне?
А)х2=![]() +3.(Так)
+3.(Так)
Б)-х2+4х=0.(Так)
В)х2+6=0.(Так)
Г) 3х2+х3-5=0.(Ні)
9. Яке з даних рівнянь є неповним квадратним?
А)х2+5х=0.(Так)
Б)![]() х2+7=0.(Так)
х2+7=0.(Так)
В)3х2+![]() =0. (Ні)
=0. (Ні)
Г) х2+ ![]() =0.(Ні)
=0.(Ні)
Д) х2+![]() =0.(Так)
=0.(Так)
Ж)3х2 +![]() =0.(Так)
=0.(Так)
10. Розв’яжіть рівняння:
А) х2 – 25=0.(![]()
Б) х2+4х=0.(0;-4)
В) х2=![]() .(
.(![]() )
)
Г) х2+9=0.
Д) х2=0.(х=0)
11.Знайти D:
А)х2-2х+1=0.( D=4 - 4![]()
Б)2х2 – х +5=0.( D=1 - 4∙2∙5= - 39)
В) х2 +4х +4=0.( D=16 - 4∙4= 0)
Запитання до теми « Функції»
1.Множина всіх значень, які може набувати функція називається ... (область значень)
2. Множина значень, які може набувати незалежна змінна називається ... (область визначення)
3. Графіком прямої пропорційності є ... (пряма)
4.Графіком квадратичної функції є ... (парабола)
5. Графіком оберненої пропорційності є (гіпербола)
6.Чи перетинає графік y=![]() вісь ОY?(Ні)
вісь ОY?(Ні)
7.В яких чвертях розміщені вітки гіперболи, якщо k![]()
8.Чи проходить графік y=![]() через точку
через точку
А) А (-1;-2) (Так);
Б) В (-2;1) (Ні).
9. Чи проходить графік функції y=x2 через початок координат? (Так)
10.Область визначення функції y=![]() є…(множина невід’ємних чисел)
є…(множина невід’ємних чисел)
11.Що більше ![]() чи
чи ![]() ? (
? (![]()
![]() )
)
12. Область значення функції y=![]() є…(множина невід’ємних чисел)
є…(множина невід’ємних чисел)
13.Чи належить графіку y=x2 точка
А) А (![]() ;
;![]() ) (Ні);
) (Ні);
Б) В (![]() ; 2) (Так).
; 2) (Так).
14.Чи належить графіку функції y=![]() точка А(-3,9)? (Ні)
точка А(-3,9)? (Ні)
15.Скільки має розв’язків рівняння :
А) x2=![]() (1);
(1);
Б) x2=![]() . (1);
. (1);
В)![]() =
=![]() . (Жодної)
. (Жодної)
16.Графіком функції у=![]() є…(ліва вітка параболи y=x2 з початком у точці О(0;0) і повернута на 90
є…(ліва вітка параболи y=x2 з початком у точці О(0;0) і повернута на 90![]()
Запитання до теми « Сюрприз» ( а в цю категорію завітали множини чисел)
- Як позначається множина раціональних чисел? (Q)
- Чи є правильно?
А)7,5 ![]()
Б) -12![]()
В) -2,7![]()
Г) 7,5 ![]()
Д) ![]()
Е) 5![]()
Ж) 0![]()
З) 45 ![]()
І) 0 ϵ Z. (Так).
3. Яка назва множин походить від слова природа?(Натуральні числа)
4. Назвіть найбільше натуральне число .( Не існує)
5. Яка назва множин походить від латинського слова, що в перекладі – відношення, частка)? (Раціональні числа)
6. Числа - ![]() ,
,![]() ,
, ![]() ,
, ![]()
7. Знайди два послідовні числа, між якими міститься число:
А)![]() . (4; 5)
. (4; 5)
Б) ![]() . (11; 12)
. (11; 12)
В)-![]() . (-6; -7)
. (-6; -7)
8.У записі: 0,(31) – у дужках записується…(Період дробу)
9.Нескінченні десяткові дроби можуть бути … (Періодичними і неперіодичними)
10. Знайдіть довжину кола радіус якого 1 см? (2![]()
11. Як записується дріб ![]() у вигляді десяткового дробу? (0,(3))
у вигляді десяткового дробу? (0,(3))
12. Що більше ?
А) 4 чи ![]() . (4
. (4![]() )
)
Б) 3 чи ![]() .( 3
.( 3![]()
![]() )
)
В)![]() чи
чи![]() . (
. (![]()
![]() )
)
ІІІ Тур. Вчитель :А ось і підійшли ми до останнього туру, який називається «А чи дружиш ти з задачами». Справжнє знання математики неможливе без вміння розв'язувати задачі. Зараз ми з вами побачимо, як наші учасники вміють розв'язувати задачі.
Задачі.
1. Яке ціле число ділиться на всі цілі числа без остачі?
2. За допомогою чотирьох п'ятірок і знаків дій та дужок запишіть число 100.
3.Задача Л.Магніцького. Знайдіть число, знаючи, що, додавши до його квадрата 108, дістанемо число в 24 рази більше від шуканого.
Підбиття підсумків.
Підбиваються підсумки змагання.
Нагороди переможців:
- «Найрозумніший учень»
- За кмітливість.
- За працьовитість.
- За наполегливість.
- За старанність.
Вчитель: Вітаємо нашого переможця, але бажаємо йому на цьому не зупинятися, а продовжувати працювати над собою і досягати все нових і нових вершин в пізнанні.


про публікацію авторської розробки
Додати розробку
