Використання інтерактивних методів навчання

у освітньому процесі з математики

 

 

 

 

 

 

 

 

Лещишин Н.В. Використання інтерактивних методів навчання у освітньому процесі з математики.   Методичний посібник /Н.В.Лещишин. – /Коцюбинське, 2022 – 35 с.

У своєму посібнику автор розглядає залежно від мети та форми організації навчальної діяльності учнів чотири групи інтерактивних технологій, а саме: інтерактивні технології кооперативного наччання; інтерактивні технології колективно-групового навчання; технології ситуативного моделювання та технології опрацювання дискусійних питань.

 У посібнику також наводяться розробки уроків з використанням інтерактивних технологій.

Посібник рекомендований для ознайомлення та використання педагогам та студентам педагогічних університетів.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Зміст

Вступ...………………………………………………………………………….4

 

І.  Сучасні підходи до організації навчання………………………………..5

1.1.Технології кооперативного навчання………………………………..5

1.2. Технології колективно-групового навчання…………………..……7

1.3. Технології ситуативного моделювання……………………….…..10

1.4. Технології навчання у дискусії………………………………….....11

 

ІІ. Конспекти уроків математики з використанням  інтерактивних технологій……………………………………………………………………………...15

2.1. Урок №1. Тема «Раціональні числа»……………………………....15

2.  Урок №2. Тема «Прямокутний трикутник»……………………....19
3.  Урок №3. Тема «Рівняння, які зводяться до квадратних»…………26
4.  Урок №4. Тема «Квадратні рівняння»……………….……………30

 

Висновки………………………………………………………….…………...34

 

Література……………………………………………………………………35

 

 

 

 

 

 

 

 

 

 

Вступ

Реформування середньої освіти і ті вимоги, що ставляться до випускників, повинні докорінно змінити навчальні методики. Сьогодні намітився перехід від авторитарної педагогіки до гуманістичного розвитку особистості, від накопичення знань до вміння оперувати знаннями, від „одноразової” освіти до безперервної, від поточної організації навчання до індивідуальної.

Одним  з генеральних завдань реформування освіти в Україні є підготовка освідченої творчої особистості, формування її фізичного і морального здоров'я. Розв'язання цієї проблеми передбачає психолого-педагогічне обгрунтування змісту і методів навчально-виховного процесу, який  скеровано на розвиток особистості учня. У зв'язку з цим  педагоги відчувають потребу у введені таких методик, які б допомогли реалізації особистісного підходу до дитини.

Сьогодні уже неможливо викладати предмети традиційно: у центрі навчального процесу знаходиться вчитель, учні слухають пояснення, виконують завдання. Введення в школі інтерактивних методик дає можливість докорінно змінити ставлення до об'єкта навчання. Підхід до учня, який знаходиться в центрі процесу навчання, базований на повазі до його думки,  на спонуканні до активності, на заохоченні до творчості. Він полягає, насамперед, у підвищенні навчально-виховної ефективності занять, і як наслідок – у значному зростанні рівня реалізації принципів свідомості, активності й якості знань, умінь і навичок. Цей підхід  має назву „навчання за методом участі” або інтерактивне навчання, коли створюється можливість обговорення кожної проблеми, доведення, аргументування власного погляду.

Суть інтерактивного навчання в тому, що навчальний процес відбувається за умови постійної, активної взаємодії всіх учасників. Воно ефективно сприяє формуванню навичок  і вмінь,  виробленню цінностей,  створенню атмосфери співробітництва, взаємодії, дає змогу педагогу стати справжнім лідером дитячого колективу.

 

 

 

 

 

І. Сучасні підходи до організації навчання

Те, що чую, я забуваю.

Те, що бачу, я пам'ятаю.

Те, що роблю, я розумію. 

Конфуцій                                                                                           

Сучасний школяр досить невиразно уявляє межі своєї інформативності, а межі пізнання наук зовсім йому не відомі. Звідкіля ж тоді взялися  допитливості, без якої будь-яке навчання – лише виховання виконавців. Головне надбання школи – це не сума вкладених у голову відповідей на стандартний перелік питань. Виправданим і привабливим видом жадібності можна назвати жагу пізнання і саморозвитку. Щоб знання перетворювалися на інструмент, учень має з ними працювати. Поки вивчення і повторення здійснюється в режимі заучування, поки перевіркою знань вважається відповідь-переказ, школа працює на 90% даремно. Що означає працювати зі знаннями? Це означає їх застосовувати, шукати умови на межі придатності, перетворювати, розширювати і доповнювати,  знаходячи нові зв'язки та співвідношення, розглядати в різних моделях і контекстах.

Основним підходом до організації систем навчання у сучасній школі  залишається класно-урочна система, за якої провідною формою організації навчальної роботи є урок. Можна виділити три основні моделі навчання : пасивну, активну та інтерактивну. Суть інтерактивного навчання в тому, що навчальний процес відбувається за умови постійної активної взаємодії всіх учасників. Його організація передбачає моделювання життєвих ситуацій, використання рольових ігор, спільне розв'язання проблеми на основі аналізу обставин та відповідної ситуації. Воно ефективно сприяє глибокому розумінню навчального матеріалу, формуванню навичок і вмінь, виробленню цінностей, створенню атмосфери співробітництва, взаємодії, розвиває мислення і мовлення, дає змогу педагогу стати справжнім лідером дитячого колективу.

Залежно від мети та форми організації навчальної діяльності учнів, інтерактивні технології можна розподілити на чотири групи:

• інтерактивні технології кооперативного навчання ;
• інтерактивні технології колективно-групового навчання;
• технології ситуативного моделювання;
• технології опрацювання дискусійних питань.

 

1.      Технології кооперативного навчання

Парна і групова робота організовується як на уроках засвоєння, так і на уроках застосування знань, умінь і навичок.  Це може відбуватися одразу ж після викладу вчителем нового матеріалу, на початку нового уроку замість опитування, на спеціальному уроці, присвяченому застосуванню знань, умінь та навичок, або бути частиною повторювально-узагальнюючого уроку.

• Робота в парах

Технологія особливо ефективна на початкових етапах навчання учнів роботі у малих групах. ЇЇ можна використовувати для досягнення будь-якої дидактичної мети: засвоєння, закріплення, перевірки знань тощо.  За умов парної роботи всі діти в класі отримують рідкісні за традиційним навчанням можливість говорити, висловлюватись. Робота в парах дає учням час обдумати,  обмінятись ідеями з партнером і лише потім озвучувати свої думки перед класом. Вона сприяє розвитку навичок спілкування, вміння висловлюватись, критичного мислення, вміння переконувати й вести дискусію. Використання такого виду співпраці сприяє тому, що учні не можуть ухилитися від виконання завдання, які за інших умов потребують великої затрати часу.

Як організувати роботу

1.               Запропонуйте учням завдання, поставте запитання для невеликої дискусії чи аналізу ситуації. Після пояснення питання або фактів, наведених  у завданні, дайте їм 1-2 хвилини для продумування можливих відповідей або рішень індивідуально.
2.              Об'єднайте учнів у пари, визначте, хто з них буде висловлюватись першим, і попросіть обговорити свої ідеї один з одним. Краще відразу визначити час на виконання кожного в пари і спільне обговорення. Це допомагає звикнути до чіткої організації роботи в парах. Вони мають досягти згоди щодо відповіді або рішення.
3.              По закінченні часу на обговорення кожна пара представляє результати роботи, обмінюються своїми ідеями та аргументами з усім класом. За потребою це може бути початком дискусії або іншої пізнавальної діяльності.

 Робота в парах – це усне або письмове виконання навчальних завдань (розв'язування задач) двома учнями в умовах синхронної роботи всіх пар.

• Робота в малих групах

Робота  в групах – це спільна діяльність для досягнення загальних цілей. За такої діяльності учні прагнуть отримати результат, що буде найкращим для кожного і для  кожного і для всіх членів групи.

Роботу в малих групах варто використовувати для вирішення складних проблем, що потребують колективного розуму.

Робота в групах передбачає розподіл класу на мікроколективи з 3 – 5 учнів. Під час розв'язування  задач „стихійно” виділяється лідер, який бере на себе інтелектуальне керівництво групою. Групові форми роботи сприяють формуванню в учневі демократичного самоусвідомлення та почуття власної гідності. Він відчуває себе вільною діючою особистістю, яка має право на вибір і ініціативу, а разом з тим готова толерантно ставитися до свого оточення, погоджувати свої дії з діями та інтересами інших членів групи.

Відкриті методики спрямовані на те, щоб не давати готових відповідей, а націлювати учнів на творчий пошук, на формування власної думки.

Навчання в групах – створення різних груп, де учні допомагають один одному й навчають один одного. Це вміння ефективно працювати в команді допомагає їм у подальшому житті.

         Як організувати роботу

1. Переконайтеся, що учні володіють знаннями та вміннями, необхідними для виконання завдання.

2.  Об'єднайте учнів у групи. Почніть із груп, що складаються з трьох учнів. П'ять чоловік – це оптимальна верхня межа для проведення обговорення в рамках малої групи.

3.   Запропонуйте усім сісти по групах. Переконайтеся в тому, що учні сидять по колу – пліч-о-пліч, один проти одного. Усі учні групи повинні добре бачити один; заохочує групу до роботи; пропонує учасникам групи висловлюватися по черзі; підбиває підсумки роботи; визначає відповідача.

Секретар: веде записи результатів роботи групи.

Посередник : стежить за часом; заохочує групу до роботи.

Доповідач : чітко висловлює думку групи; доповідає про результати роботи групи.

Вчитель : повинен поставити кожній групі конкретне завдання і дати чітку інструкцію щодо організації групової роботи.

 

2.           Технології колективно-групового навчання

 

До цієї групи входять інтерактивні технології, що передбачають одночасну спільну роботу всього класу.

 «Мікрофон»

Такий вид діяльності  надає можливість кожному сказати щось швидко, по черзі, відповідаючи на запитання або висловлюючи свою думку чи позицію.

Як організувати роботу

1.               Поставте запитання класу.
2.               Запропонуйте класу якийсь предмет (ручку, олівець тощо), який виконуватиме роль уявного мікрофона. Учні передаватимуть його один по одному, по черзі беручи слово.
3.               Надавайте слово тільки тому, хто отримує «уявний» мікрофон. Коли хтось висловлюється, інші не мають права перебивати, щось говорити, викрикувати з місця.
4.               Запропонуйте учням говорити лаконічно й швидко (не більше, ніж 0,5 – 1 хвилину).

 

 «Незакінчені речення»

Цей прийом дає можливість грунтовніше працювати над формою висловлення власних ідей, порівнювати їх з іншими. Робота за такою методикою дає присутнім змогу долати стереотипи, вільніше висловлюватися щодо запропонованих тем, відпрацьовувати вміння говорити коротко, але по суті й переконливо.

 Як організувати роботу

Визначивши тему, з якої учні будуть висловлюватись в колі ідей , учитель формулює  незакінчене речення  і пропонує учням висловлюючись закінчити його. Кожний наступний учасник обговорення повинен починати свій виступ із запропонованої формули. Учні працюють з відкритими реченнями.

 

 «Ажурна пилка»

Такий вид діяльності на уроці дає можливість працювати разом для засвоєння великої кількості інформації за короткий проміжок часу. Ефективна і може замінити лекції у тих випадках, коли початкова інформація повинна бути донесена до учнів перед проведенням основного уроку заохочує учнів допомагати один одному вчитися, навчаючи.

Як організувати роботу

1. Щоб підготувати учнів до уроку з великим обсягом інформації, підберіть матеріал, необхідний для уроку, і підготуйте індивідуальний інформаційний пакет для кожного учня.

2. Підготуйте таблички з кольоровими позначками, щоб учні змогли визначити завдання для їхньої групи. Кожен учень входитиме у дві групи – „домашню” та „експертну”. Спочатку учні об'єднуються у „домашні” групи, а потім створюються „експертні” групи, використовуючи кольорові позначки.

3. Розпишіть учнів по „домашніх” групах. Дайте домашнім групам порцію інформації для засвоєння, кожній групі – свою. Завдання домашніх груп – опрацювати надану інформацію та опанувати нею на рівні, достатньому для обміну цією інформацією з іншими.

4. Після завершення роботи  домашніх груп учні розходяться  в групи, де вони стануть експертами з окремої теми.

5. Кожна експертна група вислуховує всіх представників домашніх груп і проаналізовує матеріал в цілому, проводить експертну оцінку за певний час.

6. Після завершення роботи учням пропонується повернутися „додому”. Кожен учень ділиться інформацією, отриманою в експертній групі з членами своєї „домашньої” групи. У „домашніх” групах має бути по одній особі з експертних груп.

 

 «Мозковий штурм»

Це метод розв’язання проблеми, коли всі учасники розмірковують над однією проблемою і „йдуть на неї в атаку”. Мозковий штурм застосовують, коли треба мати кілька варіантів розв’язання конкретної проблеми. Мозковий штурм спонукає учнів проявляти уяву та творчість, дає можливість їм вільно висловлювати свої думки.

 Мета „мозкового штурму” чи „мозкової атаки” в тому, щоб зібрати якомога більше ідей щодо проблеми від усіх учнів протягом обмеженого періоду часу.

  Як організувати роботу

 Після презентації проблеми та чіткого формулювання проблемного питання (його краще записати на дошці) запропонуйте всім висловити ідеї, коментарі, навести фрази чи слова, пов’язані з цією проблемою.

 Запишіть усі пропозиції на дошці чи на великому аркуші паперу в порядку їх виголошення без зауважень, коментарів чи запитань.

 Зверніть увагу на такі моменти.

1.          Під час „висування ідей” не пропускайте жодної. Якщо ви будете судити про ідеї й оцінювати їх під час висловлювання, учні зосередять більше уваги на відстоюванні своїх ідей, ніж спробах запропонувати нові і більш досконалі.
2.          Необхідно заохочувати всіх до висування якомога більшої кількості ідей. Варто підтримувати й фіксувати навіть фантастичні ідеї. (Якщо під час мозкового штурму не вдасться одержати багато ідей, це може пояснюватися тим, що учасники піддають свої ідеї цензурі – двічі подумають, перед тим як висловлять).
3.               Кількість ідей заохочується. В остаточному підсумку кількість породжує якість. В умовах висування  великої кількості ідей учасники штурму мають можливість пофантазувати.
4.               Спонукайте всіх учнів розвивати або змінювати ідеї інших. Об’єднання або зміна висунутих раніше ідей часто веде до висунення нових, що перевершують первинні.
5.               У класі можна повісити такий плакат:

А. Кажіть усе, що спаде на думку.

Б. Не обговорюйте і не критикуйте висловлювання інших.

В. Можна запропоновувати ідеї, запропоновані будь-ким іншим.

Г. Розширення запропонованої ідеї заохочується.

6. На закінчення обговоріть й оцініть запропоновані ідеї.      

Для забезпечення швидкого та ефективного включення учнів в інтерактивну діяльність бажано давати їм пам’ятки, які містять опис алгоритму діяльності (послідовний перелік дій, які вони мають здійснювати у тій чи іншій навчальній ситуації). Такі пам’ятки можна запропонувати у вигляді роздаткового  матеріалу, плакатів або будь-якої наочності, використовуваної за допомогою технічних засобів навчання. Вони мають надаватися учням за потребою доти, доки порядок діяльності не стане для них звичним.

Варіант „мозкового штурму” – „мережа” чи „кульки”. Тут пускове слово (питання) пишеться в „кульці” в центрі сторінки. Коли обговорюються споріднені проблеми, вони записуються на папері із зазначенням зв’язку. Водночас „мозковий штурм” „вільного” типу дає можливість за дуже короткий період (три – п’ять хвилин) записати ідеї, що виникли.

 

3.           Технології ситуативного моделювання

 

Модель навчання у грі – це побудова навчального процесу за допомогою включення учня в гру.

Ігрова модель навчання покликана реалізувати, крім основної дидактичної мети, ще й комплекс цілей: забезпечення контролю  виведення емоцій; надання дитині можливості самовизначення; надихання і допомога розвитку творчої уяви; надання можливості висловлювати свої думки.

Як правило, ігрова модель навчання має чотири етапи:

1.                         орієнтація ( введення учня у тему, ознайомлення з правилами гри, загальний огляд її перебігу);
2.               підготовка до проведення гри ( ознайомлення зі сценарієм гри,  визначення ігрових завдань, ролей, орієнтовних шляхів розв'язання проблеми);
3.               основна частина – проведення гри ;
4.               обговорення.

Рольова гра стимулює прояв самостійності учнів, їх творчі можливості, гра імітує реальність шляхом „проживання ситуації у ролі”, яка учневі дісталась та надає можливості діяти ”як насправді”. Учень може поводитись і розігрувати свою роль, моделюючи реальну поведінку.

 

4.           Технології навчання у дискусії

 

Дискусії є важливим засобом пізнавальної діяльності учнів у процесі навчання. За визначенням науковців, дискусія – це широке публічне обговорення якогось спірного питання. Воно значною мірою сприяє розвитку критичного мислення, дає можливість визначити власну позицію, формує навички відстоювати свою думку, поглиблює знання з обговорюваної проблеми і все це повністю відповідає завданням сучасної школи. В дидактиці дехто з фахівців відносить дискусію як до методів навчання     (способів роботи зі змістом навчального матеріалу), так і до форм організації навчання. Певна кількість науковців вважає дискусію різновидом ігрових форм занять, співробітництва, коли з обговорюваної проблеми ініціативно висловлюють всі учасники спільної діяльності.

Сучасна дидактика визнає велику освітню і виховну цінність дискусій. Вони вчать глибокому розумінню проблеми, самостійній позиції, оперуванню аргументами, критичному мисленню, зважати на думку інших, визнавати вдалі аргументи, краще розуміти іншого, сприяють уточненню власних переконань і формуванню власного погляду на світ.

Досвід використання дискусій у навчанні дозволяє сформулювати деякі головні організаційно-педагогічні підвалини, які є спільними для будь-яких різновидів дискусії:

• проведення дискусії необхідно починати з постановки конкретного дискусійного питання;
• не слід ставити запитання на зразок: хто правий, а хто – ні в тому чи іншому питанні;
• у центрі уваги має бути ймовірний перебіг;
• усі вислови учнів мають бути у руслі обговорюваної теми;
• учитель має виправляти помилки і неточності, яких припускаються учні, та спонукати учнів робити те саме;
• усі твердження учнів повинні супроводжуватися аргументацією, обґрунтуванням;
• дискусія може закінчуватися як консенсусом, так і збереженням існуючих розбіжностей між учасниками дискусії.

 

При плануванні дискусії вчитель враховує кілька важливих моментів: час, необхідний для проведення дискусії, його узгодженість з іншими видами роботи під час навчального заняття;місце, яке має давати можливість здійснювати всі необхідні пересування учнів і створювати оптимальні умови для обговорення учнями проблеми і стеження за його перебігом решти учнів;матеріали необхідні для роботи учнів та наочного подання її результатів, письмові інструкції щодо способу виконання завдання; вміння учнів працювати в групі.

Суттєвим елементом будь-якої технології навчання в дискусії є вступна частина, оскільки саме в ній створюється емоційний та інтелектуальний настрій наступної дискусії. Це своєрідне запрошення до жвавого обговорення визначеної проблеми, яке може бути здійснено у вигляді викладу проблеми, опису конкретного випадку, невеличка рольова гра, демонстрація фільму або ілюстративного матеріалу, запрошення експертів, використання останніх новин, інсценування будь-якого епізоду.

Запорукою успішності дискусії є її чітка організація, яка досягається завдяки кільком чинникам. По-перше, це – ретельне планування дискусії. Складання плану дає змогу організувати як збирання учнями необхідної інформації, так і проведення самої дискусії. По-друге, чітке дотримання правил ведення дискусії всіма її учасниками. По-третє, обов’язковим є дотримання визначеного регламенту. Краще, коли час залишиться, ніж його не вистачить на колективне обговорення і підбиття підсумків. По-четверте, добре продумане й ефективно здійснене керівництво ходом дискусії з боку вчителя: надання учням часу для обмірковування питань; утримання від невизначених запитань та запитань подвійного змісту; зміну напряму думок учнів у разі відхилення їх від основної теми і мети дискусії; пояснення висловів дітей системою уточнюючих запитань; попередження надмірних узагальнень; збудження учнів до поглиблення думок та інші.

Згідно з логікою застосування дискусії як методу закріплення навчального матеріалу і стимулювання пізнавальної діяльності учнів можна визначити кілька варіантів моделювання навчальних тем на основі дискусії:

•             побудова вивчення теми як підготовки до дискусії за всім матеріалом, яка відбувається на останньому уроці;
•             включення дискусійного компонента в окремі уроки теми на етапах перевірки домашнього завдання і закріплення щойно вивченого матеріалу;
•             побудова навчання як самостійної або групової роботи учнів з обговоренням її результатів.

Дискусія дає прекрасну нагоду виявити різні позиції з певної проблеми або з суперечливого питання. Для того щоб дискусія була відвертою, необхідно створити в класі атмосферу довіри взаємоповаги. Тому бажано знати правила культури ведення дискусії. Учням можна запропонувати такі правила:

1. Говоріть по черзі, а не всі одночасно.
2. Не перебивайте того, хто говорить.
3. Критикуйте ідеї, а не особу, що їх висловила.
4. Поважайте всі висловлені думки (точки зору).
5. Не смійтеся, коли хтось говорить, за винятком, якщо хтось жартує.
6. Не змінюйте тему дискусії.
7. Намагайтесь заохочувати до участі в дискусії інших.

 

У кожному класі можна доповнити ці правила, прийняти їх після обговорення та дотримуватися під час проведення дискусій.

     

МЕТОД ПРЕС (PRES, МППО)

 З цієї невеличкої технології варто почати роботу над навчанням учнів дискутувати. Вона використовується при обговоренні дискусійних питань та при проведенні вправ, у яких потрібно й чітко аргументувати визначену позицію з проблеми, що обговорюється. Метод навчає учнів виробляти й формулювати аргументи, висловлювати думки з дискусійного питання у виразній і стислій формі, переконувати інших.

            Як організувати роботу

Роздайте матеріали, у яких зазаначено чотири етапи методу ПРЕС.

• Висловіть свою думку, поясніть, у чому полягає ваша точка зору

(починаючи зі слів…я вважаю, що…)

• Поясніть причину появи цієї думки, тобто на чому ґрунтуються докази (починайте зі слів…тому, що…)
• Наведіть приклади, додаткові аргументи на підтримку вашої позиції, факти, які демонструють ваші доказ (…наприклад…)
• Узагальніть свою думку (зробіть висновок, починаючи словами: отже,…таким чином…)

1.          Поясніть механізм етапів ПРЕС-методу і дайте відповідь на можливі запитання учнів. Наведіть приклад до кожного з етапів.
2.          Запропонуйте бажаючим спробувати застосувати цей метод до будь-якої проблеми на їхній вибір.
3.          Перевірте, чи розуміють учні механізм застосування методу. Етапи можна адаптувати, пропонуючи учням наводити кілька варіантів своїх думок або прикладів.
4.          Коли формула буде зрозуміла всім учням, запропонуйте їм спробуавти самим. Застосуйте метод “ПРЕС” на всіх уроках, де потрібна аргументація учнями своєї думки.

 

 

 

 

 

 

 

 

 

 

ІІ. Конспекти уроків математики з використанням  інтерактивних технологій

2.1. Урок №1. Тема «Раціональні числа»

 

Тема уроку. Урок узагальнення та систематизації знань з теми «Раціональні  числа»

Мета уроку: Узагальнити та систематизувати знання, вміння і навички учнів з теми «Раціональні числа»; сприяти активізації розумової діяльності учнів; розвивати вміння застосовувати набуті знання для досягнення поставленої мети; прищеплювати любов до математики.

Тип уроку:  урок узагальнення, систематизації та корекції знань.

Хід уроку:

І. Організація класу.

Сьогодні у нас підсумковий урок з теми «Раціональні числа». Ми маємо повторити теоретичний матеріал даної теми та його застосування при розв’язуванні вправ.

ІІ. Перевірка домашнього завдання.

Збираються робочі зошити для перевірки виконання домашнього завдання.

ІІІ. Мотивація навчальної діяльності.

Важко уявити життя людини без математики. Вона потрібна нам завжди і всюди. Без математики ми нині як без рук. А саме із нею з казки дійсність творять люди. Скажіть, будь ласка, для чого нам потрібні раціональні числа? (Учні наводять приклади використання раціональних чисел: температура, висоту предмета над рівнем моря, майно і борг, майбутній та минулий час, тощо)

Для того, щоб знати математику, треба багато працювати. Ви стараєтесь, інколи й буває важко. Однак докладаєте зусиль, і задача, яка щойно здавалася складною, вже розв’язана. Саме таким чином, за словами В.Сухомлинського, математика виховує волю і характер.

ІV. Актуалізація опорних знань.

Урок розпочнемо з повторення основних понять теми. А в цьому нам допоможе технологія «Мікрофон». Будьте уважні!

Запитання:

1. Які числа називаються додатними?

2. Які числа називаються від’ємними?

3. Що таке координатна пряма?

4. Що називають координатою точки?

5. Які числа називають протилежними?

6. Чи існує число, що дорівнює своєму протилежному числу? В разі позитивної відповіді вказати це число.

7. Які числа називаються раціональними?

8. Що називається модулем числа? Чому дорівнює модуль додатного числа, від’ємного числа?

9. Як порівняти два числа?

10. Яке з двох додатних чисел менше?

11. Яке з двох від’ємних чисел менше?

12. Що таке координати точки?

13. Які прямі називаються координатними?

14. Скількома числами визначається положення точки на координатній площині?

15. Як поділено координатну площину на чверті?

Далі показую точки на заготовленій координатній площині на дошці,  а учні по черзі (решта, кому не хватило запитань) називають їх координати.

Всі ви любите розв’язувати кросворди, читаєте дитячі газети, і навіть, я знаю, складаєте самі. А я пропоную вам кросворд незвичний – математичний. У виділених клітинках ховається прізвище видатного французького вченого-математика, яке потрібно відгадати.

		1			2
					3
4		5
6

 

                По вертикалі.

              2. Як називається число 2,  якщо дано

                  точку М(2; 1)?   (Абсциса)

              5. Як називається для тієї самої точки

                   число 1?   (Ордината)

              По горизонталі.

                1.  О(0; 0) – це … координат.   (Початок)

                3. Прямі Ох та Оу утворюють …

                    координат.    (Систему)

                4. Пара чисел (3; 6) – це … точки.                                                                    (Координати)

                6. Скільки точок задає на координатній

                   площині пара чисел?  (Одну)

З чим пов’язане прізвище цього вченого?

Де ще застосовують систему координат? (Гра в морський бій, шахи, географічні координати тощо)

Молодці! Ось ми і пригадали необхідний нам матеріал.

А тепер давайте запишемо у своїх зошитах дату сьогоднішнього уроку.

V. Розв’язування вправ.

1.     Технологія «Знайди помилку»

Вправа 1:

Знайдіть помилку в розв’язанні прикладів, виправлені записати в зошити:

а) ;           ()

б) ;           ()

в) ;                 ()

г) .              ()

2.     Робота у парах

А тепер давайте попрацюємо в парах. В парі можна спілкуватись, доводити правильність своєї відповіді. Для цього візьмемо додатковий підручник, що знаходиться на ваших столах.

Самостійна робота (тестування), виконується на два варіанти (по партах). Після закінчення роботи, діти називають отримане число.

Варіант 1: с.125, Т – V – 1.

Варіант 2: с.159, Т – V – 1.

Відповідь: Варіант 1: 32123.    Варіант 2: 11322.

3.     Технологія «Коментоване письмо»

Використовується той же підручник.

Вправа 2: (МДО – V – 3) с. 193, №1.

4.     Індивідуальна робота.  

Вправа 3:  Учні виконують самостійно запропоновані рівняння.

   Розв’язати рівняння:   а)               г)  │х│– 7 = 0;

                                                    б)  ;          д) │х – 5│– 3 = 0.

                                                    в)│х│+ 7 = 0;

 Вправа 4:     На координатній площині позначити точки: А(1; 6), В(–3; 2),  С(–3; –4), D(3; –1). Провести відрізки АС і ВD. Знайти координати точки перетину цих  відрізків. Відповідь: (–1; 1).

Вправа 5:  Позначити на координатній прямій числа, що  задовольняють нерівність:  Назвати цілі значення нерівності.      

VІ. Домашнє завдання. Повт. § 8, розв’язати № 1, 3, 5 (в – 2, с.199)

VІІ. Рефлексія (усвідомлення результатів уроку). (До 5 хвилин)

Пропоную учням оцінити результати уроку, відповівши на запитання:

•       Чи сподобався вам наш урок?
•       Чим саме?
•       Як вам працювалось в парах?
•       Які недоліки ви побачили в нашій роботі?
•       Що корисного взято із сьогоднішнього уроку?

 Дякую за урок!

 

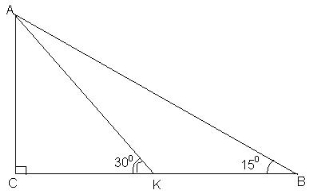
2.           Урок №2. Тема «Прямокутний трикутник».

Тема уроку:   Прямокутний трикутник

Мета уроку:  Знайти загальні методи і прийоми розв’язування типових задач, які можна використовувати під час вивчення інших розділів геометрії та розв’язування нестандартних задач.

Хід уроку

І. Вступ. Мотиваційний момент.

Учитель:  Ми продовжуємо вивчати властивості трикутників і сьогодні до нас в гості прийшов трикутник.

• Трикутником я звуся,

Мороки учням завдавати не боюся.

Сьогодні я прийшов із братом рідним –

Трикутником цікавим, своєрідним.

Ну що?  Впізнали, хто присутній?...

Так, це трикутник прямокутний!

Отже, в центрі уваги уроку – прямокутний трикутник.

Будьте готові в кінці уроку відповісти на запитання: про що дізналися? чого навчилися? чого ще не знаємо?

Оскільки в основу уроку покладено властивості прямокутного трикутника, а під час практикуму вам необхідно буде застосовувати свої знання і вміння щодо вибору різних способів розв’язання однієї задачі, повторимо необхідні математичні твердження, які є опорою в реалізації плану уроку.

Мозковий штурм

Дати відповіді на питання.

1. Який трикутник називається прямокутним?
2. Як називаються сторони прямокутного трикутника?
3. Який висновок можна зробити про властивості гострих кутів прямокутного трикутника?
4. Сформулювати властивість катета, що лежить проти кута в 30⁰.

5. Чому дорівнюють кути рівнобедреного прямокутного трикутника?

Перевірочний тест на знання властивостей прямокутного трикутника (з подальшою взаємоперевіркою)

1. Якщо один з гострих кутів прямокутного трикутника дорівнює 20⁰, то інший гострий кут дорівнює:

а) 50⁰;       б) 60⁰;      в) 70⁰.

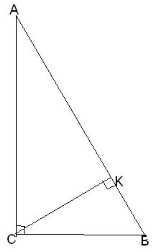
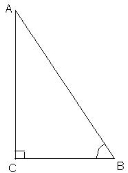
У прямокутному трикутнику  АВС відрізок  СК  є: а) висотою; б) бісектрисою; в) медіаною.

3. У прямокутному трикутнику  АВС  сторона  АВ  називається:

а) катетом;

б) гіпотенузою;

в) бічною стороною.

    4.  У прямокутному трикутнику  АВС :  ВС = 3 см;  АВ = 6 см. Знайдіть    величину кута А.

    5.  У рівнобедреному трикутнику  кути при основі дорівнюють по 45⁰. Який це трикутник?

          а) гострокутний;

          б) прямокутний;

          в) тупокутний.

     

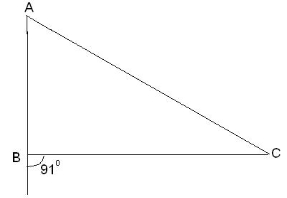
6.	Чи є трикутник  АВС  прямокутним, якщо кути  А  і   С  гострі? а) так; б) ні; в) не знаю.

 

Розв’язування усних вправ практичного змісту, що є основою для розв’язування  задач практикуму.

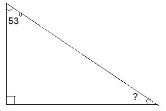
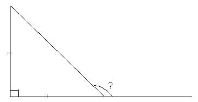
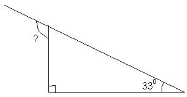
1. Знайдіть невідомий кут трикутника:

а)

б)

в)

 

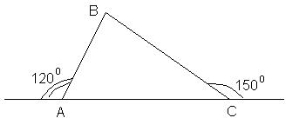
2. Чи є трикутник  АВС  прямокутним?

 

3. У прямокутному трикутнику один з гострих кутів на 40⁰ більший за другий. Знайдіть ці кути.

 

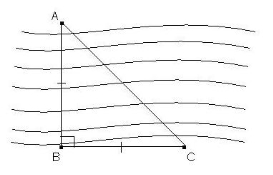
4. Геодезисти побудували такий малюнок. Поясніть, як можна знайти ширину річки.

 

      - Вивчаючи  інші властивості прямокутного трикутника, ви зможете розв’язувати задачі практичного змісту: знайти висоту пагорба або дерева.

 

ІІ. Розв’язування задач та вправ.

 

Вправа 1.

    У прямокутному трикутнику один з гострих кутів дорівнює 60⁰, а сума гіпотенузи і меншого катета дорівнює 24 см. Знайдіть гіпотенузу.

Дано:  Δ АВС;  ; ;            АВ + ВС = 24 см. Знайти:  АВ;  ВС.

 

ІІІ. Розв’язування задач практикуму «Прямокутний трикутник»

№ 1. (2 бали)

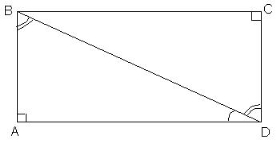
Дано: - прямокутний;            . Довести: .

                          

 Доведення:

1) В .

2)   (внутрішні різносторонні для прямих  АВ і  СD  та січної ВD)

Отже  АВ ║ СD.

 

№ 2. (2 бали)

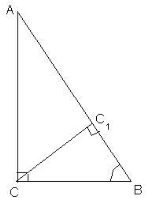
Дано:  Δ АВС;  ; ;             ;  СС1 = 2 см. Знайти:  АС.

 

 Розв’язання:

1).

2) В   . Отже  АС = 4 см.

Відповідь:  АС = 4 см.

 

№ 3. (2 бали)

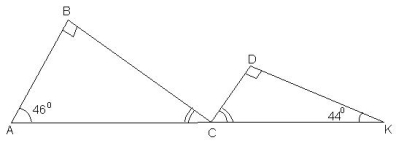
Дано: . Довести:  .

           

№ 4. (3 бали)

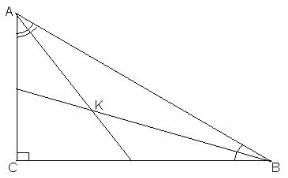
Дано: Δ АВС;  ;           АК – бісектриса кута  А;           ВК – бісектриса кута  В. Знайти:

 

 Розв’язання:

1) В Δ АВС  ()  .

Оскільки  АК – бісектриса кута  А;  ВК – бісектриса кута  В, то  .

2) В .

Відповідь: .

№ 5. (3 бали) – 2 способи

Дано:  Δ АВС;  ; ;             ;  АС = 35 см. Знайти:  ВК.

 

Розв’язання:

І спосіб:

1) суміжний з , тобто .

2) В   ,   тобто  - рівнобедрений. Отже  АК = КВ.

3) В (см).

ВК = АК = 70 см.

Відповідь:  ВК = 70 см.

 

ІІ спосіб:

1) - зовнішній кут трикутника  АКВ, тоді  .

, тобто  - рівнобедрений і  АК = ВК = 70 см.

Відповідь:  ВК = 70 см.

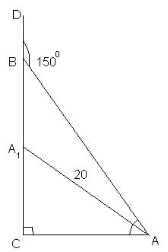
№ 6. (4 бали) – 2 способи

Дано: Δ АВС;      АА1 – бісектриса ;  АА1 = 20 см;             . Знайти:  А1С.

 Розв’язання:

І спосіб:

1) суміжний з , тоді .

2) В  Δ АВС () .

3)  АА₁ – бісектриса ; тоді  .

4) В (см).

ІІ спосіб:

1) зовнішній кут , тоді .

2)  АА₁ – бісектриса ; тоді  .

3) В (см).

Відповідь:  А₁С = 10 см.

 

IV. Домашнє завдання

Розв’язати не розв’язані  задачі практикуму.

V. Підсумок уроку:

Учитель:  Ми повторили властивості прямокутного трикутника, навчилися використовувати їх до розв’язування задач, шукати різні способи розв’язання однієї задачі, добирати раціональний спосіб.

Дайте відповіді на запитання:

1. Я дізнався на уроці ... .
2. Я повторив ... .
3. Я навчився ... .
4. Мені  ще потрібно вивчити ... (за результатами перевірочного тесту)

 

3.           Урок №3. Тема «Рівняння, які зводяться до квадратних»

 

Тема:  Рівняння, які зводяться до квадратних

Мета: формувати  вміння учнів розв'язувати рівняння, які зводяться до квадратних,  показати на прикладах різноманітність таких рівнянь та різні способи їх  розв'язання. Створити на уроці таку ситуацію, що дасть учням можливість працювати разом, творчо, мислити логічно, працювати кожному й навчати іншого, робити висновки, узагальнювати факти. У ході уроку сприяти моральному вихованню учнів.

Тип уроку : засвоєння нових знань.

 

Хід уроку

І. Актуалізація опорних знань

Квадратні рівняння люди використовують понад 4000 років. З'явившись у Вавилоні, вони здобули безсмертя і дуже часто використовуються для розв'язування математичних задач.

Репродуктивна бесіда з учнями

1. Сформулюйте означення квадратного рівняння ?

    (Усно) Із даних рівнянь назвіть квадратні :

1. 3,7х² – 5х + 1 = 0;           4) 1 – 12х = 0;
2. 48х² – х³ – 9 = 0;             5) 7х² – 13 = 0;
3. 2,1х² – 7х = 1;                 6) (х - 5)² = 0.

 

2. Яке рівняння називають неповним квадратним рівнянням ?
3. Які ви знаєте види неповних квадратних рівнянь ?

 

          (Усно)Розв'яжіть неповні квадратні рівняння :

1) 4х² = 0;                   3) х² – 4х = 0;

2) 16х² + 9 = 0;           4) 2х² – 32 = 0.

       4.  Чому дорівнює дискримінант квадратного рівняння ?

       5.  Яка залежність між його значенням і коренями квадратного рівняння ?

       6.  Яке рівняння називають зведеним ?

       7.  Яку теорему часто використовують для розв'язування зведених квадратних рівнянь ? ( теорему, обернену до теореми Вієта)

       8.  Сформулюйте теорему Вієта

            (Усно) За теоремою, оберненою до теореми Вієта, і властивістю коефіцієнтів квадратного рівняння, знайдіть корені рівняння :

1. х² – х – 2 = 0; (х₁ = -1 , х₂ = 2)
2. х² + 2х – 3 = 0; (х₁ = 1, х₂ = -3)
3. х² + 15х – 16 = 0; (х₁ = -16, х₂ = 1)
4. 5х² – 8х + 3 = 0; ( х₁ = 1, х₂ = )

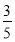ІІ. Оголошення теми і визначення очікуваних результатів уроку

«Алгебра щедра, вона часто дає більше, ніж у неї просять» -  так стверджував великий математик Д'Аламбер і наш урок буде тому підтвердженням.

Тема уроку „Розв'язування рівнянь, які зводяться до квадратних”

Очікувані результати уроку : «Сьогодні на уроці ви зможете навчитися :

•   розв'язувати біквадратні рівняння ;
•   розв'язувати рівняння, увівши нову змінну ;
•   набути навичок роботи в малих групах »

Результати вашої роботи перш за все будуть залежати від настрою на цей урок. Нехай він пройде під девізом : ( плакат вивішено на дошці)

 

ІІІ. Сприйняття і засвоєння нового матеріалу (інтерактивна технологія «робота в малих группах»)

Клас поділено на групи.

1. Учитель роздає завдання кожній групі.

 Завдання 1

Розв'яжіть рівняння:

1. 4х⁴ – 5х² + 1 = 0;    2)  х⁴ – 5х² – 36 = 0.

Завдання 2

Розв'яжіть рівняння:

1. (х² + 3)² – 11(х² + 3) + 28 = 0;    2) (2х² + 1)² = 14(2х² + 1) – 45.

Завдання 3

Розв'яжіть рівняння:

1. (х² + 6х)² + 8 (х² + 6х) = 9;     2) (х² – 5х)² – 30(х² – 5х) = 216.

Завдання 4

Розв'яжіть рівняння:

1)    2)

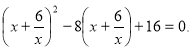
Завдання 5

Розв'яжіть рівняння:

1)      2)

2. Робота в групах – учні обмінюються інформацією, проводять обговорення розв'язків рівнянь.

3. Презентація результатів роботи (один учень біля дошки пояснює розв'язування подібного рівняння, яке було їм запропоновано )

4. Розв'язати рівняння (рівняння записані на дошці)

   1) х⁴ -13х² + 36 = 0 ; 

   2) (х² + 3х)² – 7(х² + 3х) + 10 = 0 ;

   3) (х² + 3)² – 14(х² + 3) + 24 = 0 ;

   4)

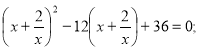
   5) +

ІV. Домашнє завдання

      Розв'яжіть рівняння:

1) х⁴ – 11х² + 18 = 0;

  2) ( 4х² - 5)² – 10(4х² - 5) - 11 = 0

  3)

V.Підсумок уроку

Учням ставляться запитання з використанням методу «мікрофон».

1. Що нового ви дізнались на уроці ?
2. Над виробленням яких навичок і вмінь працювали?
3. Що сподобалось під час уроку, що ні?
4. Як ви оцінюєте свою особисту працю на уроці ( кожен оцінює свою діяльність, дивлячись на плакат)
5.  Чи з'ясували для себе, що із вивченого потребує доопрацювання?

                                                                                                                      

 

4.           Урок №4. Тема «Квадратні рівняння».

 

Тема:   Квадратні рівняння.                             

Мета:  формування навичок розв’язування квадратних рівнянь;

            розвиток пізнавальної компетентності, логічного мислення, творчих 

            здібностей   учнів;  вміння аналізувати, вміння знаходити раціональні способи  розв’язування рівнянь; виховання самостійності, наполегливості, культури математичних міркувань, взаємоповаги.

Обладнання: картки, таблиці, підручник.

Недостатньо лише мати добрий розум,

головне – це раціонально застосувати його.

Р.Декарт.

Хід уроку.

І.   Повідомлення теми і мети уроку.

ІІ. Актуалізація опорних знань. Три учні розв’язують квадратні рівняння, записані на картках. (перевірка  домашнього завдання).

Картка № 1.

Розв’яжіть рівняння

Картка № 2.

Розв’яжіть рівняння

Картка № 3.

Розв’яжіть рівняння

Картка №4.

Знайдіть периметр квадрата, площа якого дорівнює 0,81 м². 

Історична довідка

Квадратні рівняння простіших видів вавілонські математики вміли розв’язувати ще 4 тисячі років тому. Згодом розв’язували їх також у Китаї та Греції. Особливо багато уваги квадратним рівнянням приділив Мухаммед аль-Хорезмі (ІХ ст.). Він показав як розв’язувати (при додатних а і b ) рівняння таких видів:

Від’ємних коренів тоді не знаходили. Формули коренів квадратного рівняння вивів Франсуа Вієт (1540 – 1603 ).

Використання інтерактивної технології( незакінчені речення).

1. Квадратним рівнянням називається рівняння виду...

()

2. Квадратне рівняння називається неповним, якщо... .
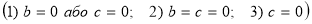3. Неповні квадратні рівняння мають вигляд... .
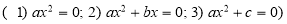4. Дискримінант квадратного рівняння обчислюється за формулою...

().

5. Дискримінант перекладається з латинської як...(розрізняючий).
6. Від знаку дискримінанта залежить... ( кількість коренів рівняння )
7. Квадратне рівняння має два корені, якщо...    ( D > 0 ).
8. Квадратне рівняння не  має коренів, якщо...    ( D < 0 ).
9. Квадратне рівняння має один корінь, якщо...    ( D = 0 ).
10. Якщо D = 0 квадратний тричлен є...  ( повним квадратом )
11. Формула коренів квадратного рівняння має вигляд... ().
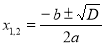12. Застосовувати даний алгоритм розв’язування до неповних квадратних рівнянь... (можна, але не раціонально ).

Усно розв’язати  неповні квадратні рівняння

1)   ; 2)  ;  3)  .

ІІІ. Розв’язування рівнянь з використанням формули дискримінанта

 Картка №5.

Розв’яжіть квадратні рівняння.

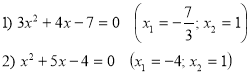
Картка №6.

Розв’яжіть квадратні рівняння.

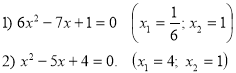
Картка №7.

Розв’яжіть квадратні рівняння.

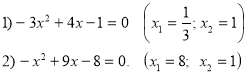
Картка №8.

Розв’яжіть квадратні рівняння.

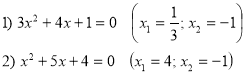
Картка №9.

Розв’яжіть квадратні рівняння.

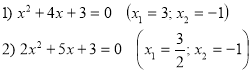
 ІV.  Вивчення нових властивостей квадратного рівняння.

Ці рівняння вибрані не випадково.

Чи мають однаковий корінь дані рівняння?

Чому він дорівнює?

У картках 5 – 7:

Знайдіть значення виразу для цих рівнянь

Знайдіть взаємозв’язок між коефіцієнтами а,b,с.    ()

Як пов’язані корені рівняння з коефіцієнтами  а,b,с ?  ( )

У картках 8 – 9:

Знайдіть взаємозв’язок між коефіцієнтами а,b,с.    ( )

Як пов’язані корені рівняння з коефіцієнтами  а,b,с ?  ( )

Узагальнимо

                     

              якщо                                   

               то                                      

 

V. Підсумок уроку

1.   Повторили...  (алгоритми розв’язування квадратних рівнянь )

2.   Вивчили нову... ( властивість квадратного рівняння )

3.   Усна довідка: дізнались... ( про деякі історичні факти щодо призначення квадратних     рівнянь )

VІ. Оцінювання

VІІ. Домашнє завдання. Скласти на вивчені властивості по три квадратні рівняння і знайти їх корені; §40, розв’язати №№330(а), 333(а), 334(а).

 

 

 

 

 

 

 

Висновки

Таким чином, ми застосували кілька інтерактивних методів на уроках математики, поєднуючи з традиційними методами навчання. Кожний з перелічених методів учить дитину мислити самостійно, працювати в колективі, критично міркувати (так як він не завжди погоджується з „обраною" позицією).

Найкориснішим при такому навчанні є те, що зникають негативні відповіді про предмет, адже немає нічого складного, коли вчити разом зі своїм товаришем; можеш його виправити, а він може щось підказати. Система уроків з математики, проведена за інтерактивними технологіями, дозволяє нам зробити висновки про те , що це надзвичайно цікаві для дітей уроки, які сприяють активізації навчання школярів, здружують їх, формують у них відповідальність за себе і за колектив, покращують мовленнєві здібності,тощо.

Використання в роботі технології інтерактивного навчання дає учневі:

• розвиток особової рефлексії;
• усвідомлення включеності  в загальну роботу;
• становлення активної суб'єктної позиції в учбовій діяльності;
•  розвиток навиків спілкування;
• ухвалення моральності норм і правил спільної діяльності;
•  підвищення пізнавальної активності класу:
• формування класу як груповій спільності;
• підвищення пізнавального інтересу;
• розвиток навиків аналізу і самоаналізу в процесі групової рефлексії; вчителеві:
• нестандартне відношення до організації освітнього процесу;
• формування мотиваційної готовності до міжособової взаємодії не тільки в учбових, але і інших ситуаціях.

З набуттям практичного педагогічного досвіду неодноразово змінювалися мої погляди на процес освіти.

З технології інтерактивного навчання я узяла багато нового і корисного для свого професійного зростання, для вирішення проблеми активізації пізнавальної діяльності дітей. Учні з року в рік стають дорослішими, розвинутішими за допомогою нетрадиційного підходу до навчання. Вони здатні працювати вже не на репродуктивному рівні, а творити. Завдяки технології співпраці вони стають самостійнішими, активнішими, товариськими і здатними працювати на більш високому рівні.

Створюється ситуація мого творчого зростання, завдяки якій я виходжу на вищий виток свого професійного розвитку.

 

 

 

Література

1. Бабкина Н.В. Нетрадиционный курс «Развивающие игры с элементами логики» для первых классов начальной школы. // Психологическое обозрение. 1996. № 2 (3), с. 47-52.
2. Г.П.Бевз. Алгебра: Проб. підруч. для 7 – 9 кл. серед. шк. – 2-ге вид. – К.: Гімназія, 2001
3. Зайцев Т.Г. Теоретические основы обучения решению задач в начальной школе. – М.: Педагогика, 1983.
4. Зак А.З. 600 игровых задач для развития логического мышления детей. Ярославль: «Академия развития», 1998.
5. Зак А.З. Развитие умственных способностей младших школьников. М.: Просвещение, Владос, 1994.
6. Колінець Г.Г. Формування дослідницьких здібностей у старшокласників // Обдарована дитина. – 1999. – №5. – с. 10-13.
7.  Кремінський Б.Г. Обдарованість та проблема розвитку здібностей особистості // Практична психологія та соціальна робота. – 2004. - №12. – с.74-80.
8. Кричевец А.Н. О математических задачах и задачах обучения математике // Вопросы психологии. – 1999. - № 1. – с.32-42.
9. Липина И. Развитие логического мышления на уроках математики // Начальная школа. – 1999. - № 8. С. 37-39.
10. Лихтарников Л.М. Занимательные логические задачи. Для учащихся начальной школы. – СПб.: «Лань», «Мик», 1996.
11. Лукавецький В.І., Маланюк М.П. Завдання з математики для 4 і 5 класів: Методичний посібник – Київ: Радянська школа, 1987. – 207 с.
12. Мерзляк А. Г., Полонський В. Б., Рабінович Ю. М., Якір М. С. Збірник задач і завдань для тематичного оцінювання з алгебри для 7 класу. — X.: Гімназія, 2010. — 112 с.
13. Мойсеєнко Л.А. Творче математичне мислення: психологічна сутність/ Л.А.Мойсеєнко // Обдарована дитина. – 2007. - №7. – с.20-29.
14. Монько О. Плекаємо творчого учня/ О. Монько // Математика [газета]. – 2008. – Квітень (№14). – с.1-7.
15. О.Померун, Л.Пироженко, Сучасний урок. Інтерактивні технології навчання. Київ «А.С.К.» 2005
16.  Освітні технології: Навч.-метод. посіб. / О. М. Пєхота, А. 3. Кіктенко, О. М. Любарська та ін.; За заг. ред. О. М. Пєхоти. — К.: А.С.К., 2001. — 256 с.
17. Практикум з методики навчання математики. Загальна методика: Навч. посібник для організації самостійної роботи студентів математичних спеціальностей педагогічних університетів / З.І.Слєпкань, А.В.Грохольська, В.Я.Забранський, С.М.Лук’янова, Л.Л.Панченко, І.С.Соколовська. За ред. З.І.Слєпкань. – К.: НПУ імені М.П.Драгоманова, 2006. – 392 с.