Інтерактивний підручник "Комбінації з кулею"
Про матеріал
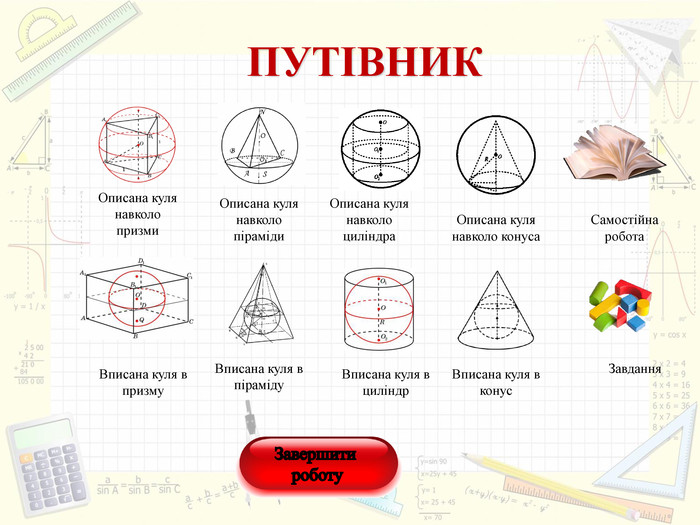
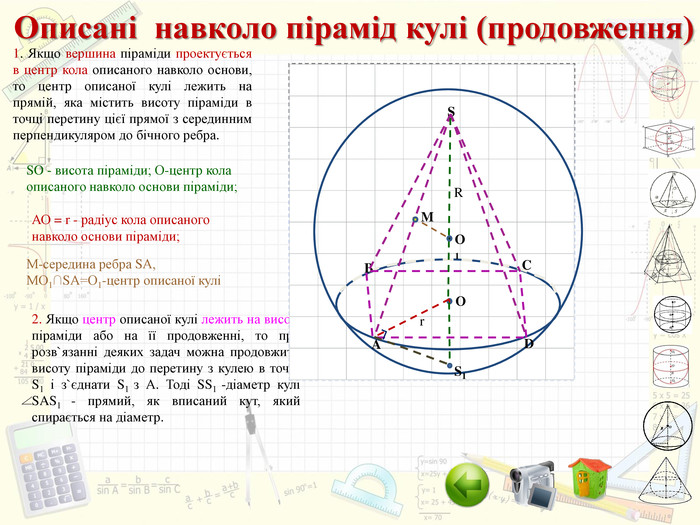
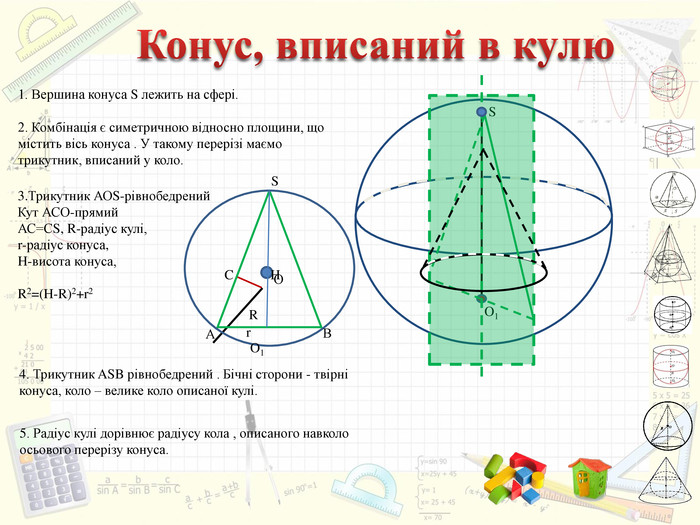
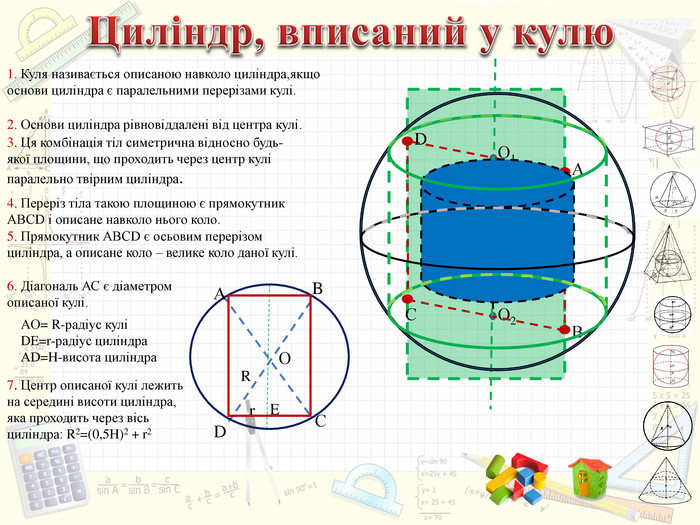
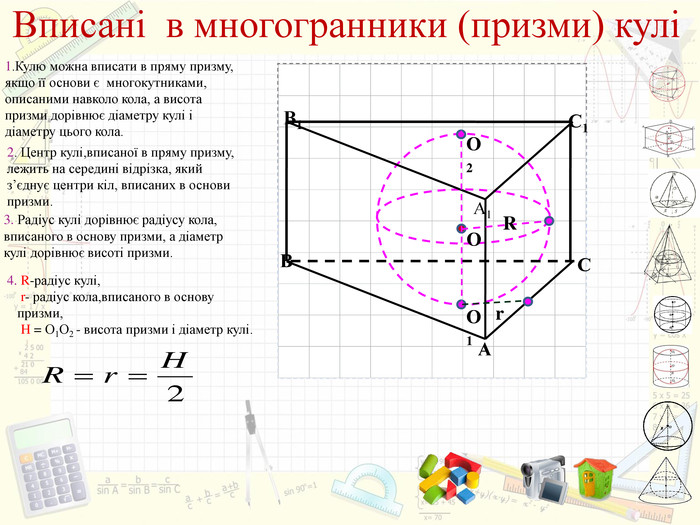
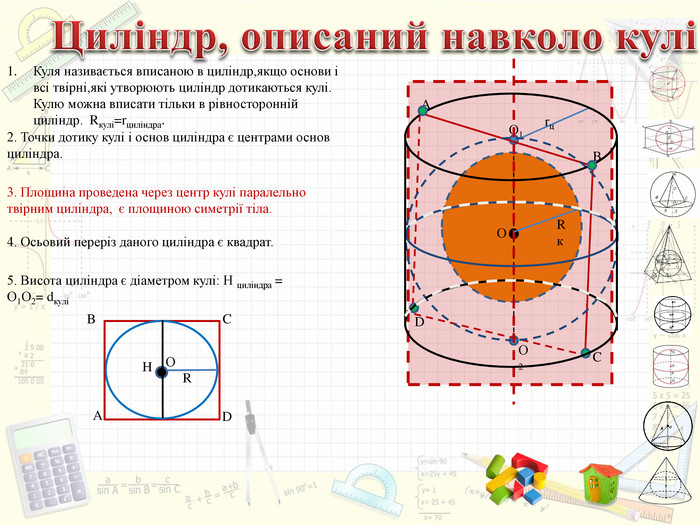
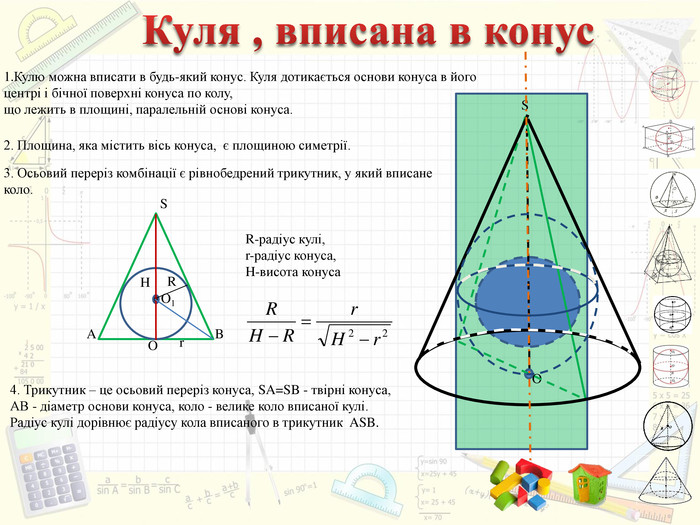
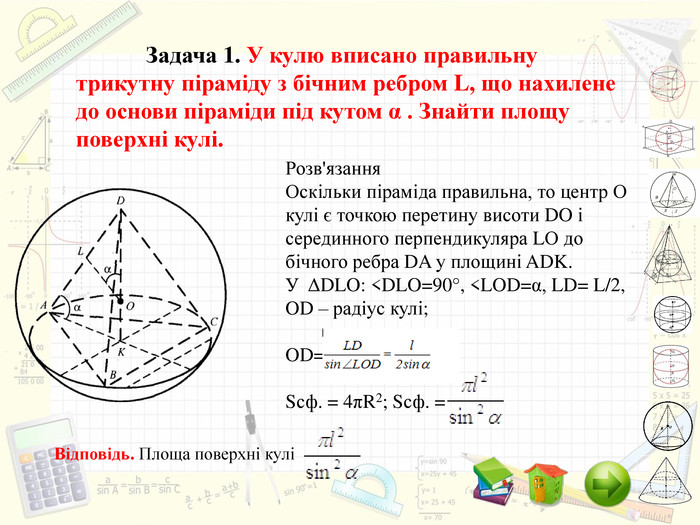
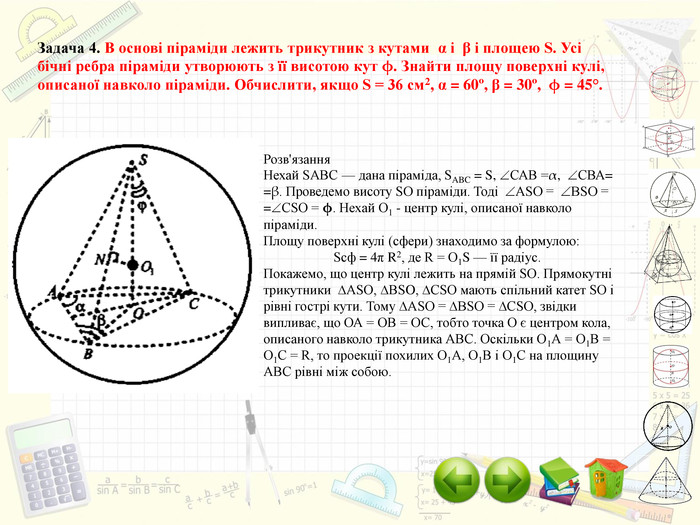
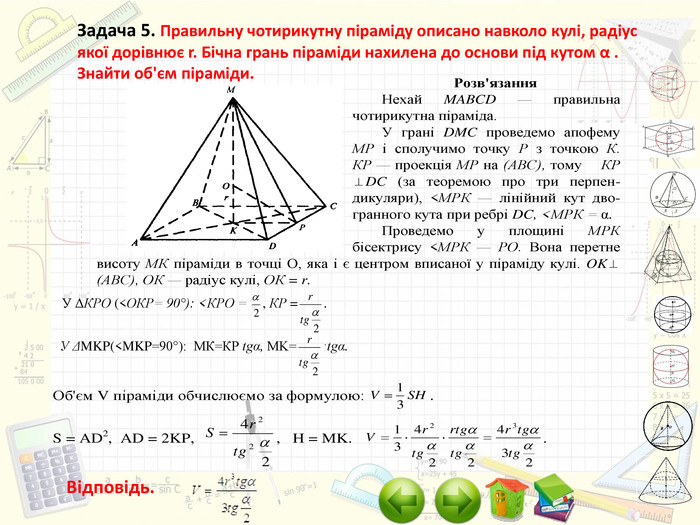
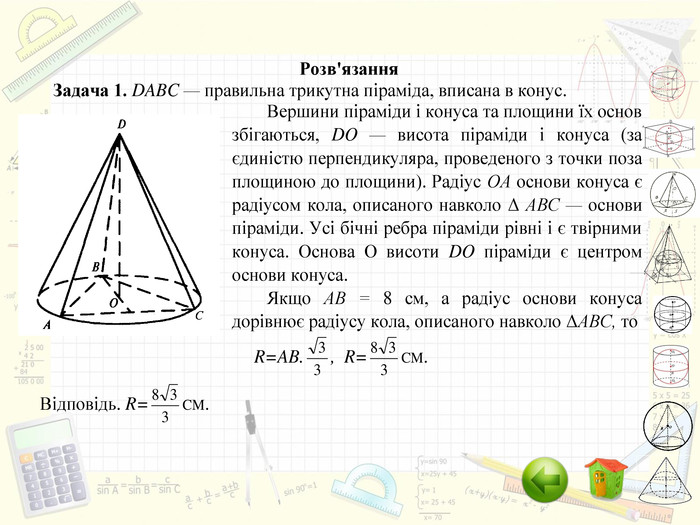
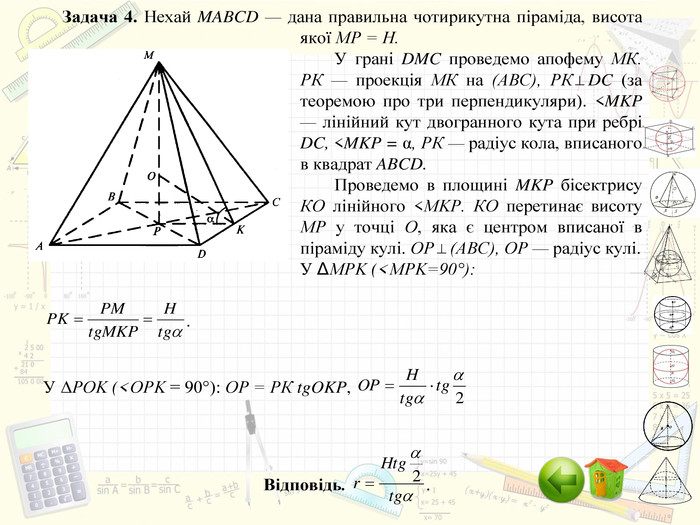
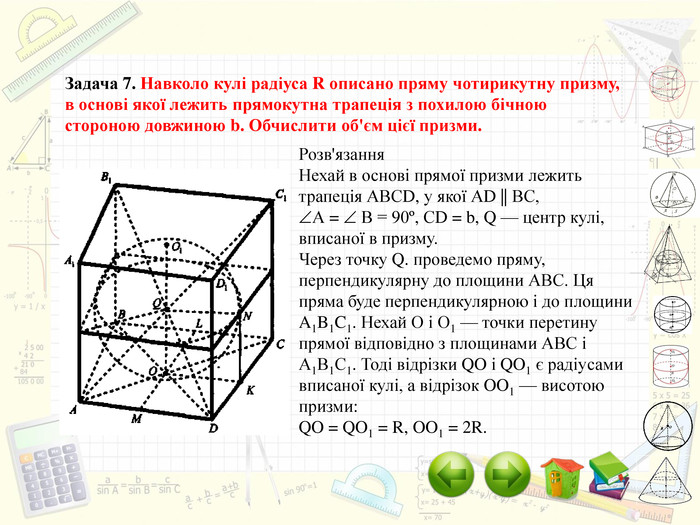
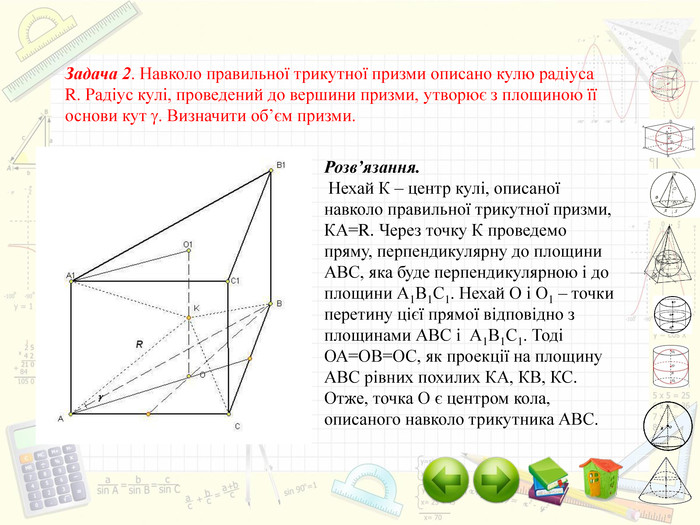
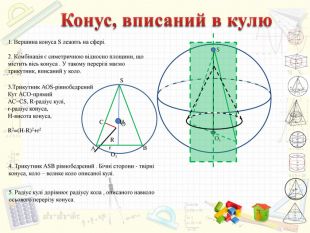
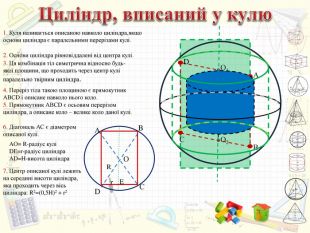
Інтерактивний підручник з теми "Комбінації геометричних тіл з кулею", який спонукає учнів до самостійного засвоєння знань і вмінь з даної теми, містить багато зображень, відео, містить повні розв'язання задач, завдання для самостійного розв'язання. Зміст архіву
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Дякую!! Величезна робота!!!
-
Дуже потужний матеріал, дякую за працю
zip
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку