Презентація "Перерізи многогранників та тіл обертання"

Перерізи многогранників та тіл обертання. Геометрія. 11 клас. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

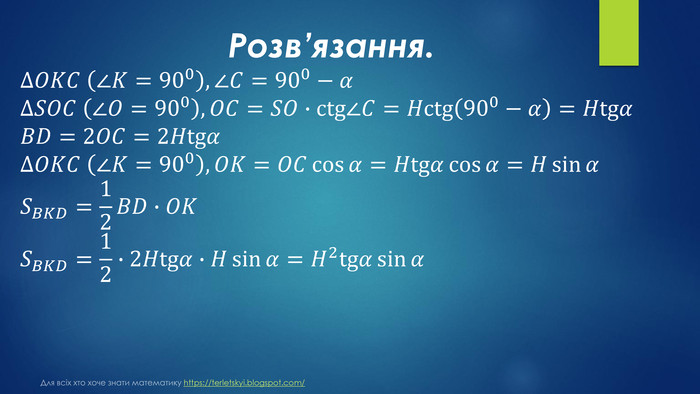
Мета уроку:навчальна: систематизувати, узагальнити знання учнів про многогранники та тіла обертання, формувати вміння і навички зображати перерізи многогранників та тіл обертання;розвивальна: удосконалювати навички застосовувати основні властивості многогранників та тіл обертання під час розв’язування задач, здатності до самостійного мислення, розвивати пам’ять, увагу;виховна: формувати працьовитість, прищеплювати бажання мати якісні, глибокі знання, виховувати культуру математичних записів та інтерес до вивчення предмету. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

Актуалізація знань. Паралелепіпед Призма. Піраміда Зрізана піраміда. Циліндр Конус. Зрізаний конус Куля. Сфера. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

Завдання з вибором однієї правильної відповідіДля всіх хто хоче знати математику https://terletskyi.blogspot.com/

№ 17, 2013_ІПереріз кулі площиною має площу 81π см2. Знайдіть відстань від центра кулі до площини перерізу, якщо радіус кулі дорівнює 15 см.{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД6 см8 см9 см12 см15 см. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

Відповідь: ГРозв’язання. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

№ 25, 2011 Діагональним перерізом правильної чотирикутної призми є прямокутник, площа якого дорівнює 40 см2. Периметр основи призми дорівнює 202 см. Визначте висоту призми. {2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД2 см22 см4 см1 см2 см{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД4 см1 см2 см. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

Відповідь: ВРозв’язання. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

№ 12, 2010_ІНа рисунку зображено куб ABCDA1 B1 C1 D1. Перерізом куба площиною, що проходить через точки А, С, С1 єА прямокутний трикутник. Б рівносторонній трикутник. В прямокутник. Г ромб. Д трапеція. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

Відповідь: ВРозв’язання. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

№ 8, 2010_ІІОсьовим перерізом циліндра є прямокутник, діагональ якого дорівнює 10 см. Знайдіть радіус основи циліндра, якщо його висота дорівнює 8 см.{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД1 см2 см3 см6 см12 см. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

Відповідь: ВРозв’язання. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

Завдання на встановлення відповідностіДля всіх хто хоче знати математику https://terletskyi.blogspot.com/

На рисунку зображено циліндр, радіус основи якого дорівнює 6, а висота – h, Чотирикутник ABCD – осьовий переріз цього циліндра. До кожного початку речення (1–4) доберіть його закінчення (А–Д) так. щоб утворилося правильне твердження. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

№ 24, 2016д. Початок речення Закінчення речення1 Периметр чотирикутника ABCD А h = 3 дорівнює 36, якщо Б h = 3,52 Площа чотирикутника ABCD В h = 4 дорівнює 42, якщо Г h = 4,53 Об'єм циліндра дорівнює 108π, якщо Д h = 64 Площа бічної поверхні циліндра дорівнює 48π, якщо. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

Розв’язання.1. 𝑃𝐴𝐵𝐶𝐷=22𝑟+h; 36=212+h,  h=6.2. 𝑆𝐴𝐵𝐶𝐷=2𝑟h; 42=12h,  h=3,5.3. V=π𝑟2h,  108𝜋=𝜋36h,  h=3.4. 𝑆б.п.=2𝜋𝑟h, 48𝜋=2𝜋∙6h, h=4.  Відповідь: 1 – Д, 2 – Б, 3 – А, 4 – В. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

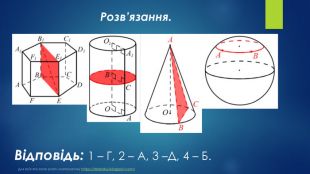
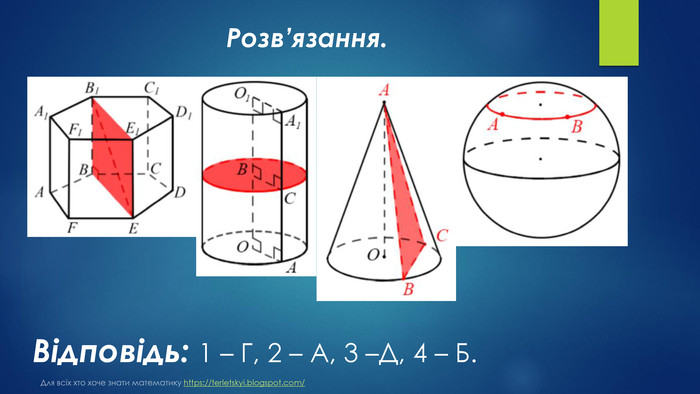
№ 28, 2010_ІІУстановіть відповідність між перерізами геометричних тіл (1–4) та їхніми назвами (А–Д). Переріз Назва перерізу1 діагональний переріз правильної шестикутної призми А круг2 переріз циліндра площиною, що перетинає його Б коло твірну і перпендикулярна до неї В шестикутник3 переріз конуса площиною, що проходить через його Г прямокутник вершину та хорду основи Д трикутник4 переріз сфери площиною, що проходить через дві різні точки сфери. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

Розв’язання. Відповідь: 1 – Г, 2 – А, 3 –Д, 4 – Б. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

Завдання відкритої форми з короткою відповіддю. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

№ 35, 2015_ІОсновою прямої чотирикутної призми ABCDA1 B1 C1 D1 є прямокутник зі сторонами 4см і 43 см. Площина, що проходить через вершини А, В1 і С призми, утворює з площиною її основи кут 60°. Визначте висоту призми (у см). Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

Розв’язання. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

Розв’язання. Відповідь: 6 Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

№ 33, 2014 Через точки А і В, що лежать на колах верхньої та нижньої основ циліндра і не належать одній твірній, проведено площину паралельно осі циліндра. Відстань від центра нижньої основи до цієї площини дорівнює 2 см, а площа утвореного перерізу – 602 см2. Визначте довжину відрізка АВ (у см), якщо площа бічної поверхні циліндра дорівнює 203𝜋 см2. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

Розв’язання. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

Розв’язання. Відповідь: 18 Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

№ 31, 2012_ІОсновою прямої призми ABCDA1 B1 C1 D1 є рівнобічна трапеція ABCD. Основа AD трапеції дорівнює висоті трапеції і в шість разів більша за основу ВС. Через бічне ребро СС1 призми проведено площину паралельно ребру АВ. Знайдіть площу утвореного перерізу (у см2), якщо об'єм призми дорівнює 672 см3, а її висота – 8 см. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

Розв’язання. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

Розв’язання. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

Розв’язання. Відповідь: 104 Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

№ 31, 2012_ІІОсновою прямої трикутної призми АВСА1 В1 С1 є рівнобедрений трикутник ABC, де АВ = ВС = 25 см, АС = 30 см. Через бічне ребро АА1 призми проведено площину, перпендикулярну до ребра ВС. Визначте об'єм призми (у см3), якщо площа утвореного перерізу дорівнює 72 см2. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

Розв’язання. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

Розв’язання. Відповідь: 900 Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

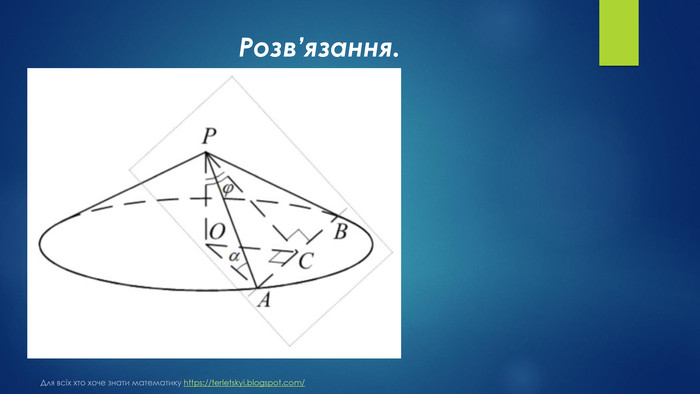
№ 31, 2009 Радіус основи конуса R, твірна нахилена до площини основи під кутом α. Через вершину конуса проведено площину під кутом φ до його висоти. Ця площина перетинає основу конуса по хорді. Знайдіть площу утвореного перерізу. У відповідь запишіть значення знайденого виразу при 𝑅=6, 𝛼=300, 𝜑=450. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

Розв’язання. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

Розв’язання. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

Розв’язання. Відповідь: 4 Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

№ 34, 2008 У правильній трикутній піраміді SABC з основою ABC бічне ребро удвічі більше за сторону основи. Точки К і L є серединами ребер АС і ВС відповідно. Через пряму KL паралельно до ребра SC проведено площину а. Знайдіть кут φ між площиною а і площиною (ABC). У відповідь запишіть значення 3cos2𝜑. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

Розв’язання. Відповідь: 0,25 Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

Завдання відкритої форми з розгорнутою відповіддю. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

№ 32, 2019д. У конусі радіус основи дорівнює 𝑅, твірна – 𝑙. Через вершину конуса й хорду його основи проведено площину 𝛽. Ця площина утворює з площиною основи гострий кут 𝛼.1. Зобразіть переріз конуса площиною 𝛽 та вкажіть його вид.2. Обґрунтуйте положення кута 𝛼.3. Визначте периметр цього перерізу. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

Розв’язання.1. Перерізом конуса є рівнобедрений трикутник 𝐴𝑆𝐵.2. 𝑆𝐾⊥𝐴𝐵𝑂𝐾⊥𝐴𝐵⇒∠𝑆𝐾𝑂=𝛼.3. ∆𝑆𝑂𝐴∠𝑆𝑂𝐾=900, 𝑆𝐴2=𝑆𝑂2+𝑂𝐴2т. Піфагора,𝑆𝑂=𝑙2−𝑅2.∆𝑆𝑂𝐾∠𝑆𝑂𝐾=900,sin∠𝑆𝐾𝑂=𝑆𝑂𝑆𝐾⇒𝑆𝐾=𝑙2−𝑅2sin𝛼. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

Розв’язання.∆𝑆𝐾𝐴∠𝑆𝐾𝐴=900, 𝑆𝐴2=𝑆𝐾2+𝐴𝐾2т. Піфагора,𝐴𝐾=𝑙2−𝑙2−𝑅2sin2𝛼=𝑙2sin2𝛼−𝑙2+𝑅2sin2𝛼==𝑙2sin2𝛼−1+𝑅2sin2𝛼=𝑅2−𝑙2cos2𝛼sin𝛼.𝑃𝐴𝑆𝐵=2𝑆𝐴+𝐴𝐵=2𝑆𝐴+2𝐴𝐾,𝑃𝐴𝑆𝐵=2𝑙+2sin𝛼𝑅2−𝑙2cos2𝛼. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

№ 32, 2019 У нижній основі циліндра проведено хорду 𝐴𝐵, довжина якої дорівнює 𝑐. Цю хорду видно із центра верхньої основи під кутом 𝛼. Через хорду 𝐴𝐵 проведено площину 𝛽 паралельно осі циліндра на відстані 𝑑 (𝑑≠0) від неї.1. Зобразіть переріз циліндра площиною 𝛽 та вкажіть його вид.2. Обґрунтуйте відстань 𝑑.3. Визначте площу цього перерізу. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

Розв’язання.1. Перерізом циліндра є прямокутник 𝐴𝐵𝐶𝐷.2. 𝑂𝐴=𝑂𝐵𝑂𝑂1||𝐴𝐵𝐶𝐷⇒𝑂𝐾⊥𝐴𝐵, 𝑂𝐾=𝑑.3. 𝑂1𝐴=𝑂1𝐵⇒∠𝐴𝑂1𝐾=12∠𝐴𝑂1𝐾=𝛼2.∆𝐴𝐾𝑂1∠𝐾=900, tg∠𝐴𝐾𝑂1=𝐴𝐾𝑂1𝐾⇒𝑂1𝐾=𝑐2tg𝛼2=𝑐ctg𝛼22. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

Розв’язання.∆𝑂1𝑂𝐾∠𝑂=900, 𝑂1𝐾2=𝑂1𝑂2+𝑂𝐾2т. Піфагора,𝑂1𝑂=𝑐2ctg2𝛼24−𝑑2=𝑐2ctg2𝛼2−4𝑑24=𝑐2ctg2𝛼2−4𝑑22.𝐴𝐷=𝑂1𝑂.𝑆𝐴𝐵𝐶𝐷=𝐴𝐵∙𝐴𝐷=𝑐∙𝑐2ctg2𝛼2−4𝑑22=𝑐2𝑐2ctg2𝛼2−4𝑑2 Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

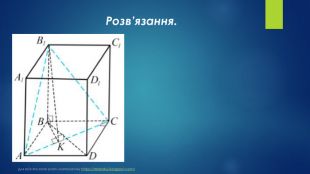
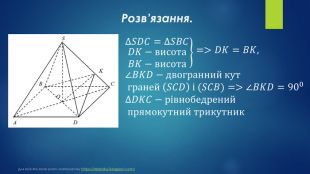
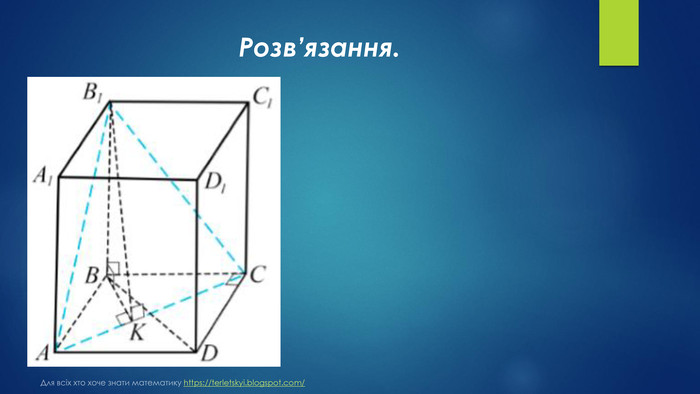
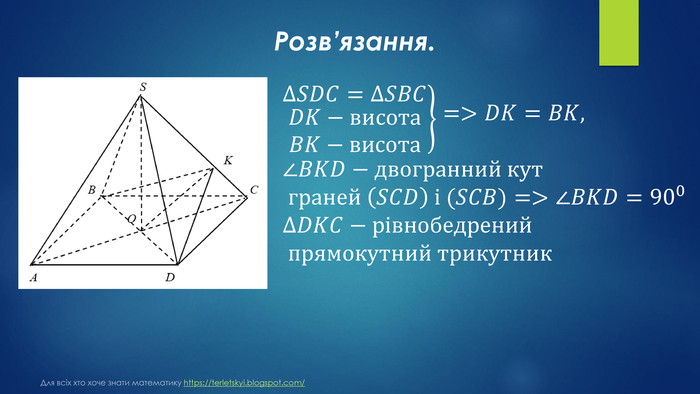
№ 32, 2018д. У правильній чотирикутній піраміді 𝑆𝐴𝐵𝐶𝐷 через діагональ 𝐵𝐷 основи перпендикулярно до бічного ребра 𝑆𝐶 проведено площину 𝛾. Ця площина утворює з площиною основи кут 𝛼. Висота піраміди дорівнює 𝐻.1. Побудуйте переріз піраміди 𝑆𝐴𝐵𝐶𝐷 площиною 𝛾.2. Обґрунтуйте вид перерізу.3. Визначте площу перерізу. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

Розв’язання. ∆𝑆𝐷𝐶=∆𝑆𝐵𝐶𝐷𝐾−висота𝐵𝐾−висота=>𝐷𝐾=𝐵𝐾,∠𝐵𝐾𝐷−двогранний кут граней 𝑆𝐶𝐷 і (𝑆𝐶𝐵)=>∠𝐵𝐾𝐷=900∆𝐷𝐾𝐶−рівнобедрений прямокутний трикутник  Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

Розв’язання.∆𝑂𝐾𝐶 ∠𝐾=900, ∠𝐶=900−𝛼∆𝑆𝑂𝐶 ∠𝑂=900, 𝑂𝐶=𝑆𝑂∙ctg∠𝐶=𝐻ctg900−𝛼=𝐻tg𝛼𝐵𝐷=2𝑂𝐶=2𝐻tg𝛼∆𝑂𝐾𝐶 ∠𝐾=900, 𝑂𝐾=𝑂𝐶cos𝛼=𝐻tg𝛼cos𝛼=𝐻sin𝛼𝑆𝐵𝐾𝐷=12𝐵𝐷∙𝑂𝐾𝑆𝐵𝐾𝐷=12∙2𝐻tg𝛼∙𝐻sin𝛼=𝐻2tg𝛼sin𝛼 Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

№ 32, 2018 У правильній чотирикутній піраміді SABCD сторона основи ABCD дорівнює с, а бічне ребро SA утворює з площиною основи кут α. Через основу висоти піраміди паралельно грані ASD проведено площину β.1. Побудуйте переріз піраміди SABCD площиною β.2. Обґрунтуйте вид перерізу.3. Визначте периметр перерізу. Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

Розв’язання. 𝐷𝑁=𝑁𝐶𝑁𝐿||𝐷𝑆=>𝑁𝐿−середня лінія ∆𝐷𝑆𝐶,𝑁𝐿=12𝐷𝑆𝐴𝑀=𝑀𝐵𝑀𝐾||𝐴𝑆=>𝑀𝐾−середня лінія ∆𝐴𝑆𝐵,𝑀𝐾=12𝐴𝑆𝑁𝐿=𝑀𝐾𝑀𝑁||𝐾𝐿=>𝑀𝐾𝐿𝑁−рівнобічна трапеція Для всіх хто хоче знати математику https://terletskyi.blogspot.com/

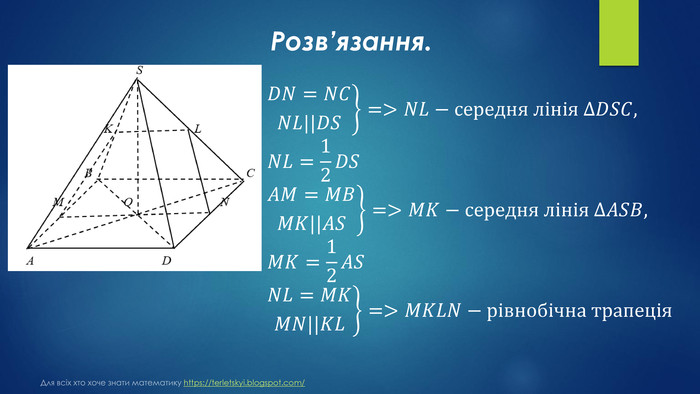
Розв’язання.𝑁𝐿−середня лінія ∆𝐷𝑆𝐶𝑀𝐾−середня лінія ∆𝐴𝑆𝐵=>𝐶𝐿=𝐿𝑆𝐵𝐾=𝐾𝑆=>𝐾𝐿−середня лінія ∆𝐵𝑆𝐶,𝐾𝐿=12𝐵𝐶𝑀𝑁=𝐵𝐶=𝑐,𝐾𝐿=12𝑐;𝑂𝐷=𝐴𝐷22=𝑐2∆𝑆𝑂𝐷: cos𝐷=𝑂𝐷𝑆𝐷=>𝑆𝐷=𝑂𝐷cos𝐷, 𝑆𝐷=𝑐2cos𝛼, 𝐿𝑁=𝑐22cos𝛼𝑃=𝑀𝑁+𝐾𝐿+2𝐿𝑁,𝑃=𝑐+12𝑐+𝑐2cos𝛼=2𝑐∙cos𝛼+c∙cos𝛼+𝑐22cos𝛼==𝑐2cos𝛼+cos𝛼+22cos𝛼=3cos𝛼+22cos𝛼∙ Для всіх хто хоче знати математику https://terletskyi.blogspot.com/