Урок. Тема "Трикутник. Піраміда.Конус"

 

11 клас

 

Тема.  Трикутник. Піраміда. 

                         Конус

 

 

 

 

 

Тема:

Трикутник. Піраміда. Конус

 

Мета уроку:

• Повторити, систематизувати і узагальнити теоретичні та практичні знання з тем «Трикутник», «Піраміда», «Конус».
• Відпрацювати роботу з тестовими завданнями.
• Стимулювати раціональне використання часу; введення ігрового моменту для зняття нервово-психологічного напруження; розвивати пізнавальні процеси, пам'ять, мислення, увагу, спостережливість; виробити самооцінку у виборі напрямку; критерії оцінки своєї роботи та роботи товариша; збільшити інтерес учнів до завдань тестової форми; сформувати в них позитивний мотив навчання.

   .    Тип уроку:

    Урок узагальнення та систематизації отриманих раніше знань.

Організаційні форми спілкування:

     Індивідуальна, по два, по три, група.

Структура уроку:

1. Мотиваційна бесіда з постановкою мети(замисел гри).
2.  Вхідний контроль, презентація, практична частина для кожної  підтеми  уроку.
3. Підсумковий тест узагальнюючий знання за даними тем.
4. Домашнє завдання.
5. Рефлексія.

 

 

 

 

Хід уроку

І.  Мотиваційна бесіда

ІІ. Повідомлення правил уроку та гри

                                           «Немає іншої науки, яка б підносила їх крок за кроком на дедалі вищі сходинки творчого мислення, як математика».

                                                           Джеймс Сильвестр   

Сьогодні ми будемо крок за кроком повторювати, закріпляти знання з тем: «Трикутник. Піраміда. Конус», а також готуватись до Зовнішнього Незалежного оцінювання виконуючи завдання в тестовій формі.

Один звук – це ще не мелодія, мелодія – це зібрання звуків. Ось і ми зберемо нотки знань і об’єднаємо їх в єдину мелодію:«Я знаю. Я вмію. Я використовую»

Наш урок розбитий на чотири частини: І – трикутник, ІІ – піраміда, ІІІ – конус і ІV – підсумкова де ми об’єднаємо все те що повторили.

На при кінці кожної частини ви повинні відгадати мелодію цього етапу.

І так починаємо І частину уроку. «Трикутник» , що ви про нього знаєте, дасть можливість дізнатися перший тест для всієї команди.       

 

 

Трикутники

                                      Тест  1(теорія).

( Для всієї групи )

1. Трикутник, у якого дві сторони рівні, називаються… (Рівнобедреним)
2. Трикутник у якому всі кути рівні, тобто по 60º називається… (Рівносторонній)
3. В рівнобедреному трикутнику ку ти при основі…(рівні)
4. Сума кутів будь-якого трикутника дорівнює…(180º)
5. Відношення протилежного катета до прилеглого в прямокутному трикутнику називається…(Тангенсом кута)
6.  В прямокутному трикутнику: сума квадратів катетів дорівнює…(Квадрату гіпотенузи)
7. Якщо в задовільному трикутнику відомі всі сторони відомі то його площу можна знайти за  формулою… (S=√p(p-a)(p-b)(p-c))
8. Радіус описаного навколо прямокутного трикутника кола дорівнює… (Половині гіпотенузи)

 

Так як ця команда зробила перша цей тест назвіть відповіді, а друга - перевіряє.  Після цього ви можете виставити перші бали в свої особисті картки.

Де що ви згадали за допомогою тестів, дещо вам допоможе згадати Сергій зі своєю презентацією цієї теми.

Закріпимо тему «Трикутник» індивідуальним завданням в тестовій формі.

 

 

 

 

 

 

 

 

 

Тест  2(практика)

І.

1.Медіана, опущена на гіпотенузу прямокутного трикутника, дорівнює 2,5см,а один із катетів дорівнює 4см. Обчисліть довжину другого катета.

А	Б	В	Г	Д
1см	3см	1,5см	9,6см	4см

 

2.У рівносторонньому трикутнику висота дорівнює √3см. Обчисліть довжину сторони трикутника.

А	Б	В	Г	Д
4см	3см	6см	2√3см	2см

 

3.Сторони трикутника, одна з яких на 4см більше за другу, утворюють кут 120º, а довжина третьої сторони дорівнює 14см. Знайдіть периметр трикутника.

А	Б	В	Г	Д
32см	30см	42см	36см	28см

 

4.Коло радіуса 7см описане навколо трикутника АВС кут АСВ=30º. Знайдіть довжину сторони АВ.

 

А	Б	В	Г	Д
1,75см	3,5см	7см	14см	7√3см

 

5. Периметр трикутника дорівнює 20дм, а його площа – 18дм². Обчисліть радіус кола, вписаного в цей трикутник.

А	Б	В	Г	Д
5∕ 9дм	20∕ 9дм	0,9дм	1,8дм	3,6дм

 

6.Гіпотенуза прямокутного трикутника дорівнює 5см, а один з катетів – 4см. Знайти периметр трикутника.

А	Б	В	Г	Д
12см	18см	24см	9см	48см

 

ІІ.

1.Знайдіть медіану рівностороннього трикутника зі стороною 2√3см.

А	Б	В	Г	Д
2см	3см	1см	√3см	1,5см

 

2.Один із катетів прямокутного трикутника дорівнює 2, а прилеглий до нього гострий кут - 60º. Знайдіть периметр трикутника.

А	Б	В	Г	Д
2+2√3	8	6+2√3	(9+4√3) ∕ 3	4+4√3

 

3.Бічна сторона рівнобедреного трикутника дорівнює 30см, а довжина бісектриса, опущеної на основу, - 18см. Знайдіть довжину основи трикутника.

А	Б	В	Г	Д
48см	12см	24см	52см	68см

 

4.Площа рівностороннього трикутника дорівнює 4√3см². Знайдіть сторону трикутника.

А	Б	В	Г	Д
2√2см	8см	4см	2√3см	2√6см

 

5.Гіпотенуза прямокутного трикутника дорівнює 16см. Обчисліть площу круга, описаного навколо цього трикутника.

А	Б	В	Г	Д
1024πсм²	16πсм²	32πсм²	8πсм²	64πсм²

 

6.Гіпотенуза прямокутного трикутника дорівнює 13см,а один із катетів – 12см. Знайдіть периметр трикутника.

А	Б	В	Г	Д
30см	26см	50см	27см	40см

 

 

Після проведення останнього тесту  для кожної команди вмикається фрагмент пісні(кількість секунд відповідає кількості правильних відповідей за сумою двох тестів).              

Піраміда

Тест  1(теорія).

(завдання для всієї команди)

1. Многогранник, одна грань якого – п-кутник, а інші п граней – трикутники із спільною вершиною, називається… (Пірамідою)
2. Якщо в основі піраміди лежить правильний п-кутник то ця піраміда називається…(Правильною)
3. Перпендикуляр, проведений з вершини піраміди до площини основи, називається…(Висотою піраміди)
4. Висота бічної грані правильної піраміди, що проведена з її вершини, називається…(Апофемою)
5. Якщо Sбіч. = SΔSAB + SΔSBC  + SΔSAC, то для правильної піраміди  Sбіч. = …(Росн. ·h  ∕ 2, де h – апофема )
6. Sповн. = … + … (  Sбіч. + Sосн. )                                  

                  S                       

7.  

 

                                                                               Об’єм піраміди       SABC знаходиться за допомогою формули… (V = Sповн.·r ∕3)

 

 

 

 

 

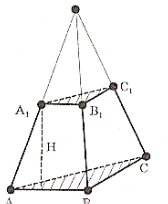
8. Яка це піраміда?(Зрізана)

Після перевірки результати заносяться в особисті картки учнів, а також в картку команди.

 

Презентація даної теми.(останній лист, з формулами, залишається на екрані і учням дається листи з умовою Теста 2(практика).

Тест  2(практика)

(кожна задача на двох учнів)

 

1. Відстань від точки до площини трикутника дорівнює 12см, а радіус вписаного в цей трикутник кола дорівнює 5см. Знайдіть відстань від точки до сторін трикутника, якщо ці відстані рівні.

А	Б	В	Г	Д
√119см	17см	15см	16см	13см

 

2. Скільки площин визначають чотири точки, які не лежать водній площині?

А	Б	В	Г	Д
Дві	Три	Чотири	Безліч	Одну

3. Знайдіть довжину сторони основи правильної піраміди з об’ємом 4√3 і висотою 3.

А	Б	В	Г	Д
2√2	(4√3) ∕ 3	4	6	8

Завдання відкритої форми з короткою відповіддю.

(кожна задача для трьох учнів)

 

4. Сторони основи правильної трикутної піраміди дорівнює 6см, а бічне ребро – (2√30) ∕3см. Знайдіть об’єм піраміди(у см³).(6)

 

5. Сторона основи правильної трикутної піраміди дорівнює 6см, а апофема - √39 ∕ 3см. Знайдіть об’єм піраміди(у см³).(6)

 

Після проведення останнього тесту  для кожної команди вмикається фрагмент пісні(кількість секунд відповідає кількості правильних відповідей за сумою двох тестів).

 

КОНУС

Тест 1(теорія).

(всій команді)

1. Фігуру, яку отримали при обертанні прямокутного трикутника навколо своєї осі(одного з катетів), називають…(конусом)
2. Катет трикутника, що належить осі обертання, називають…(висотою конуса), гіпотенуза прямокутного трикутника – це…(твірна конусу)
3. Якщо відомо твірна конусу та радіус основи конуса, то бічну й повну поверхні конусу можна знайти за формулами…  (Sбіч.=πRL, Sповн.=πR(R+L), де R – радіус основи, L – твірна).
4. Тіло обертання, що утворене обертанням прямокутної трапеції навколо меншої бічної сторони, називають… (зрізаним конусом)
5.  Знайдіть помилку: V=πRH  (V=πR²H ∕ 3)

 

 

Після перевірки результати заносяться в особисті картки учнів, а також в картку команди.

 

Презентація даної теми.(останній лист, з формулами, залишається на екрані і учням дається листи з умовою Теста 2(практика).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тест 2(практика)

(кожна задача на двох учнів)

1. Знайдіть висоту конусу, радіус основи якого дорівнює 4см, а площа бічної поверхні - 20πсм².

А	Б	В	Г	Д
5см	2см	2,5см	3см	2√21см

 

2. Знайдіть висоту конуса, об’єм якого дорівнює 21πсм³, а радіус основи – 6см.

А	Б	В	Г	Д
7 ∕ 12см	1,75см	5,25см	10,5см	3,5см

 

3. Трикутник АВС (АВ=1, ВС=2, АС=√5) обертається навколо сторони ВС. Яке тіло утворюється в результаті обертання?

А	Б	В	Г	Д
Не утворюється ніякого, бо трикутника з такими сторонами не існує	Конус	Два конуси	Циліндр	Інше тіло

Завдання відкритої форми з короткою відповіддю.

(кожна задача для трьох учнів)

 

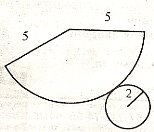4.    На рисунку зображено розгортку конусу. Визначте відношення площі повної поверхні цього конуса до площі його бічної поверхні.  (1,4)                 
5. У кулю радіусом 6√2 вписано конус, твірна якого нахилена під кутом 45º до площини основи. Обчисліть твірну конуса.(12)

 

Після проведення останнього тесту  для кожної команди вмикається фрагмент пісні(кількість секунд відповідає кількості правильних відповідей за сумою двох тестів).

 

 

Підсумкова задача

В кулю вписана правильна чотирикутна піраміда, яка має двогранний кут при основі, що дорівнює α. Площа кулю дорівнює S, знайти площу основи піраміди.

Розв’язання:

Нехай SАВСD – дана піраміда, вписана в кулю. Площина основи піраміди перетинає кулю по колу, що описане 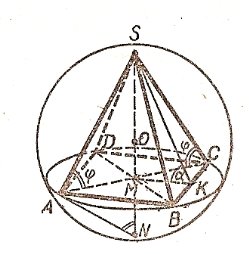                                               навколо квадрата  АВСD (основа висоти піраміди є центром  цього кола).

З теореми про перетин кулі випливає, що перпендикуляр SМ до площини АВС проходить крізь центр О кулі.

Розглянемо ∆SАС:

Позначимо SАМ через φ. Точка О належить площині SАС, тоді ∆SАС вписаний у велике коло кулі; діаметром цього кола є відрізок SN.

З прямокутного трикутника SАN та SМА мають:

SNА=φ,SА=SN∙sinSNА=2R sinφ;

АМ= АS∙sinSАМ=2R∙ sinφcosφ=R∙ sin2φ. Тоді Sосн.=½АС∙ВD=½∙(АС)²=2 R²∙ sin²2φ. За умовою 4πR²=S, тоді R²=S ⁄ 4π  і   Sосн.= (S∙ sin²2φ) ⁄ 4π .

Площу основи  ми знайшли, але необхідно кут φ виразити  через кут α. З прямокутних трикутників SМС та SМК знайдемо їх спільну сторону SМ. З ∆SМС маємо: SМ=МСtg φ. З  ∆SМК:  SМ=МКtgα.

З цього  МСtg φ= МКtgα. Але МС=МК√2,

тоді √2tg φ=tgα, tgα= tg φ ⁄ √2. За  sinφ=(2tg φ) ⁄ (1+ tg² φ)

отримаємо

                  sinφ=(2√2tg φ) ⁄ (2+ tg² φ) .

 З цього випливає

                                 Sосн.= (4tg² φ) ⁄ π (2+ tg² φ).

Після проведення останнього тесту  для кожної команди вмикається фрагмент пісні(кількість секунд відповідає кількості правильних відповідей) – супер - гра Підсумковий тест

1. Сума кутів трикутника...(180°)
2. Відомо дві сторони і кут трикутника, третю сторону можна знайти за формулою...(а²=в²+с²-   

    -2вс·cosα).

3.В трикутнику відомо  сторона та висота, опущена на цю сторону, площу можна знайти за формулою... (S=½·аha)

4.Теорема Піфагора: квадрат гіпотенузи дорівнює… (сумі квадратів катетів)

5.Центр описаного навколо трикутника кола, є точка перетину…(серединних перпендикулярів)

6.Висота бічної грані піраміди називається… (апофемою)

7.Об’єм піраміди :…(V=⅓∙SОСН.∙Н)

        8. Фігуру, яку отримали при обертанні прямокутного   

        трикутника навколо своєї осі(одного з катетів),

        називають…(конусом)

9.Площа повної поверхні конуса… (Sповн.=πR(R+L), де R – радіус основи, L – твірна)            

ІІІ. Домашня робота

4. Рефлексія