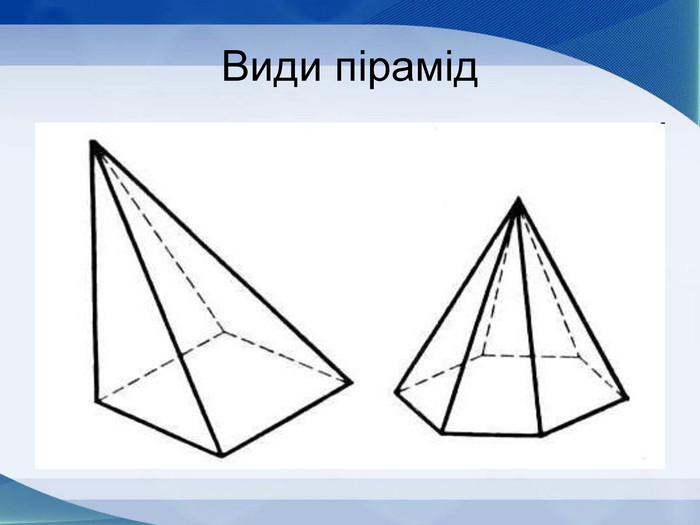
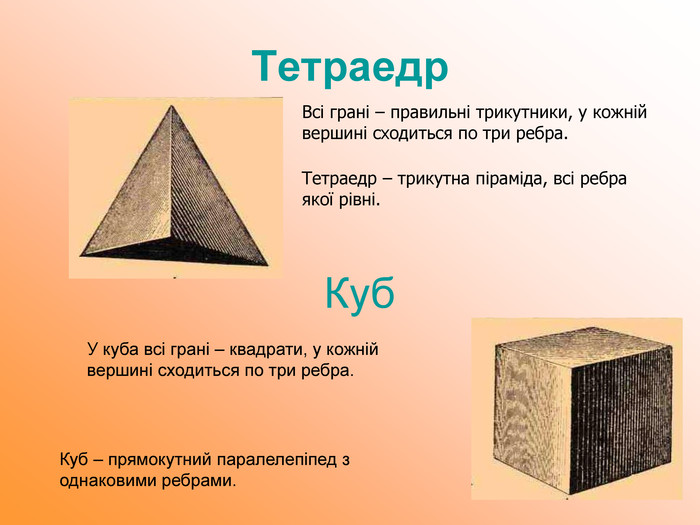
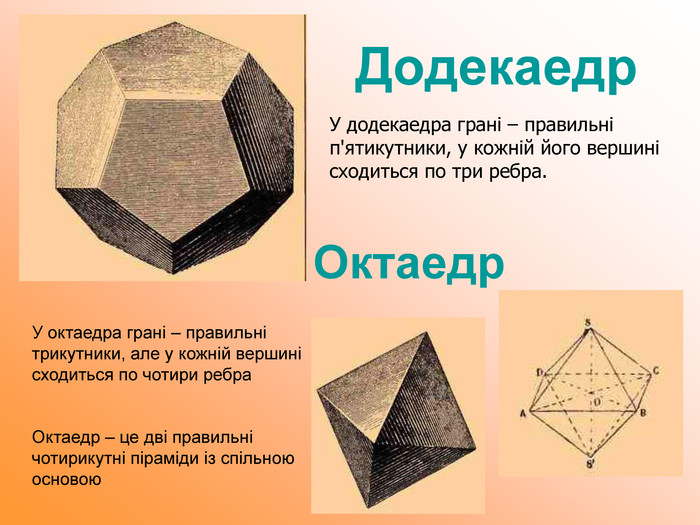
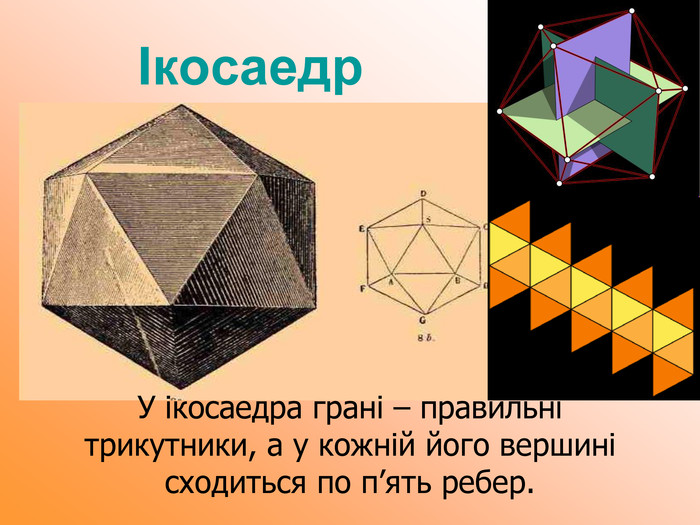
Презентація до уроку геометрії "Многогранники"
Про матеріал
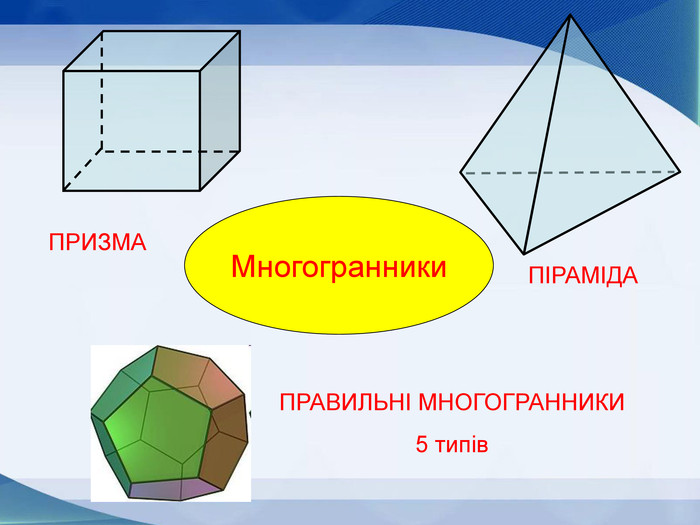
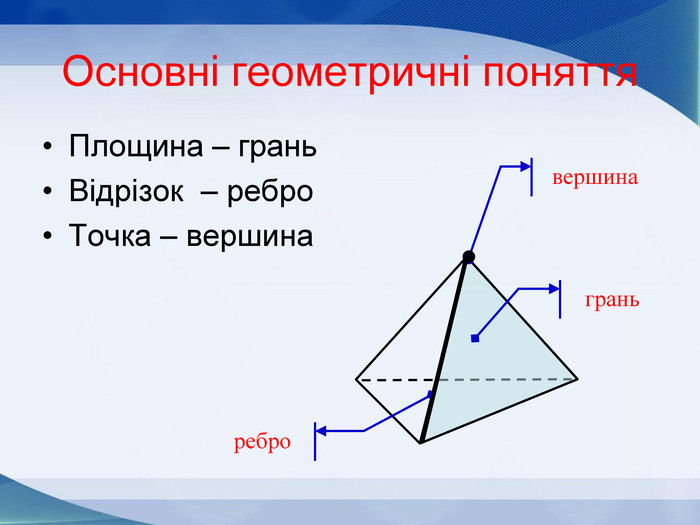
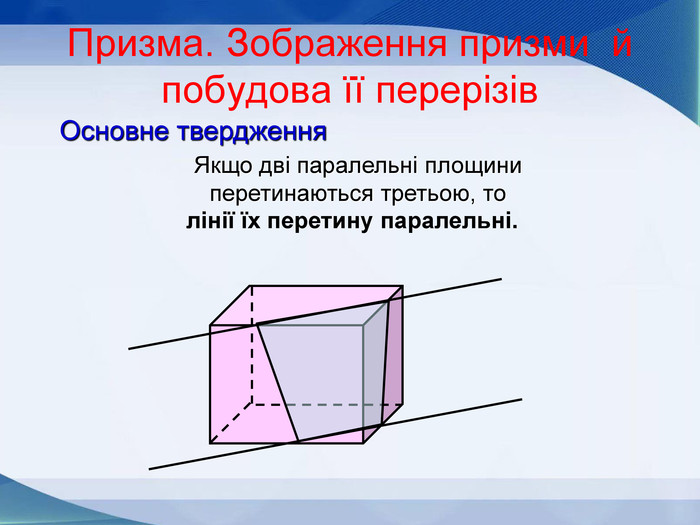
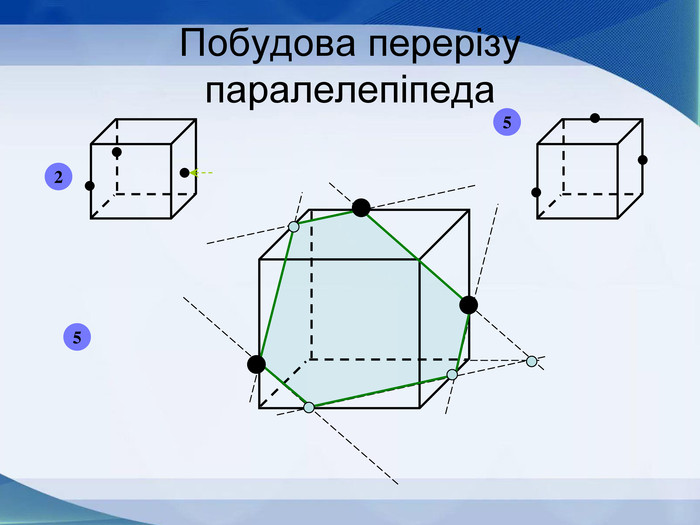
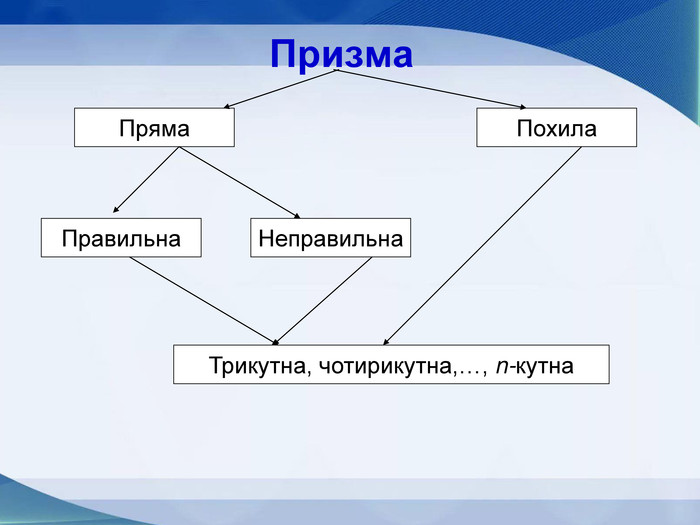
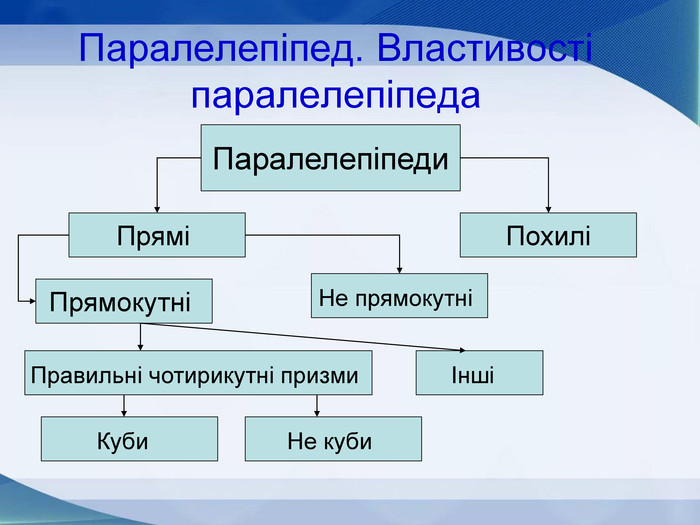
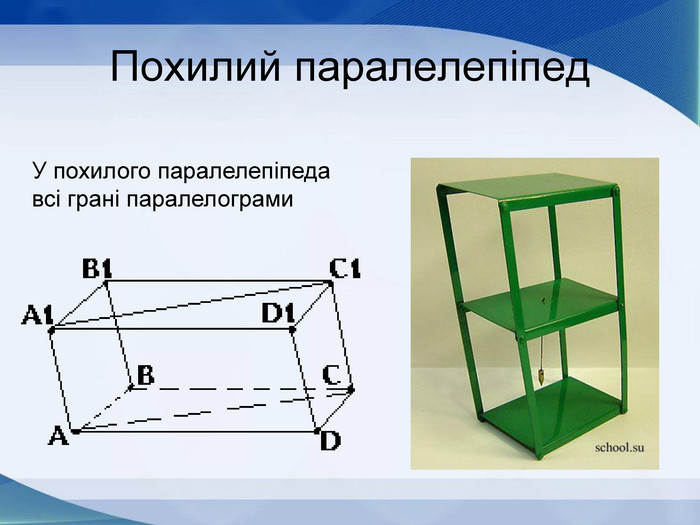
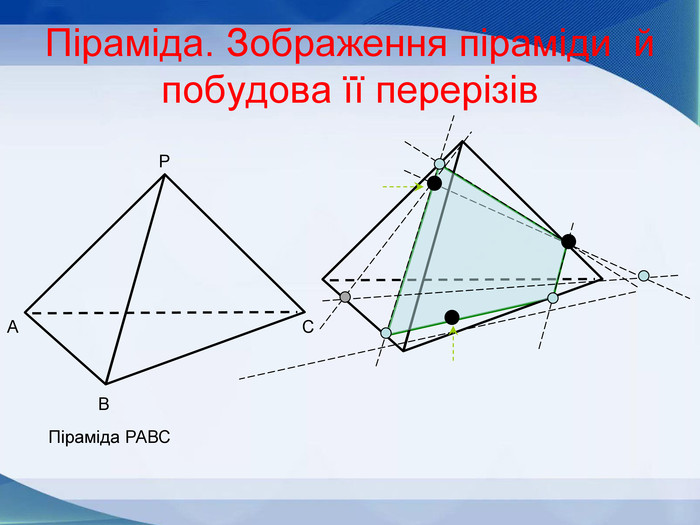
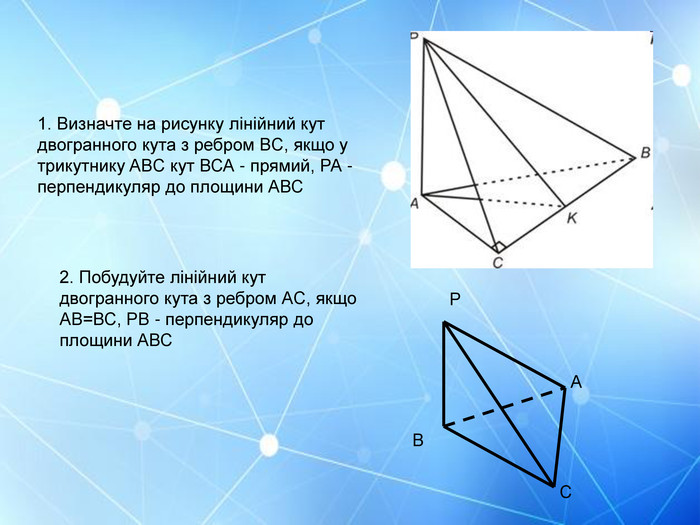
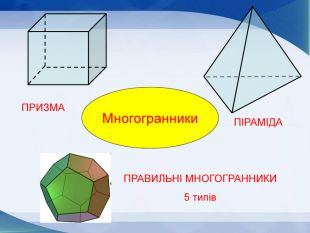
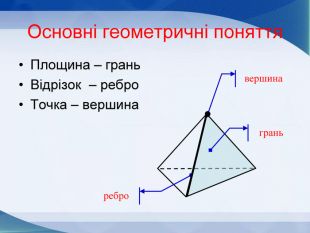
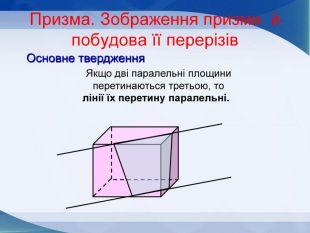
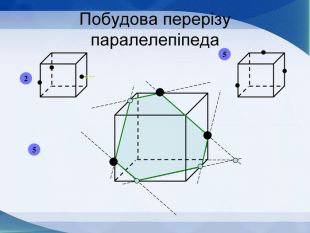
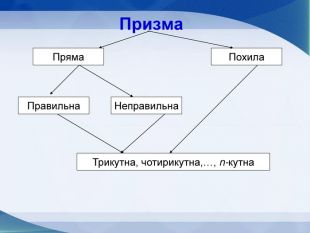
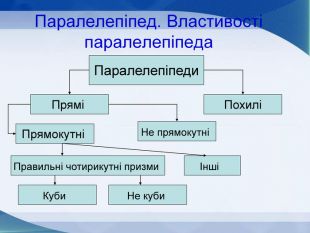
Мета презентації узагальнити й розширити знання учнів про многогранники та їх види; розвивати логічне мислення, просторову уяву, креслярські навички, інтуїцію; показати нерозривний зв’язок даної теми з життям; прослідкувати міжпредметні зв’язки.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Дякую за чудову роботу!
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку