Ірраціональні нерівності. Розвязування ірраціональних нерівностей

Тема: ірраціональні нерівності.

Мета: сформувати в учнів уявлення про ірраціональну нерівність та навчити розв’язувати ірраціональні нерівності вигляду .

Тип уроку: засвоєння знань, формування вмінь.

Література:

• Для вчителя:

1. Бевз Г.П. Алгебра: підручник для кл. з поглиб. вивч. матем 10 кл. – К.: Генеза, 2010. – 342 с.
2. Математика. Комплексне видання: Довідник з математики. 5 – 11 класи. Аналіз найпоширеніших помилок. Тестові завдання/ О.С. Будна, С.М. Будна, А.Р. Гальперіна, М.Я. Забєлишенська, О.Я Михеєва. – Х.: «Літера» ЛТД, 2009. – 320 с.

• Для учнів:

1. Бевз Г.П. Алгебра: підручник для кл. з поглиб. вивч. матем 10 кл. – К.: Генеза, 2010. – 342 с.

Структура уроку

1. Організаційний етап        (2 хв.)
2. Перевірка домашнього завдання      (10хв.)
3. Актуалізація опорних знань       (11хв.)
4. Вивчення нового матеріалу       (20хв.)
5. Засвоєння вмінь та навичок       (30хв.)
6. Підбиття підсумків уроку       (5хв.)
7. Домашнє завдання        (2хв.)

Хід уроку

1. Організаційний етап

Перевірка готовності учнів до уроку, налаштування на роботу.

2. Перевірка домашнього завдання
3. Актуалізація опорних знань

Фронтальне опитування

1.               Які нерівності називаються рівносильними? Які рівносильні пе­ретворення нерівностей ви знаєте? Наведіть приклади.
2.               Що означає розв’язати нерівність? Що означає розв’язати систему нерівностей? Поясніть хід розв’язування системи нерівностей.
3.               У чому полягає метод інтервалів розв’язування нерівностей? Наведіть приклад нерівності, яку доцільно розв’язувати методом інтервалів, і поясніть хід розв’язування такої нерівності.

4. Вивчення нового матеріалу

Способи розв'язання ірраціональних нерівностей:

1.               Розв’язування найпростіших ірраціональних нерівностей.

          , розв’язків немає

Приклад 1. Розв’яжіть нерівність .

Розв’язання. Задана нерівність рівносильна нерівності .

Відповідь: .

2.               Спосіб рівносильних перетворень:

1.              
2.               .

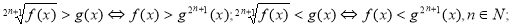
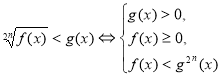Приклад 2. Розв’яжіть нерівність .

Розв’язання. Нерівність рівносильна системі нерівностей:

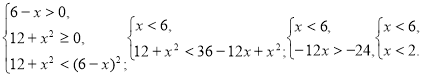
Відповідь: .

Приклад 3. Розв’яжіть нерівність .

Розв’язання. Нерівність рівносильна сукупності нерівностей

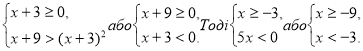
Відповідь: .

3.               Метод інтервалів.

Приклад 4. Розв’яжіть нерівність .

Розв’язання. ОДЗ нерівності . Задана нерівність рівносильна нерівності . Позначимо . Нулі функції . На області визначення функції позначимо її нулі й на здобутих проміжках визначимо знаки функції:

Відповідь: .

5. Засвоєння вмінь та навичок.

Виконання усних вправ:

1.               Укажіть область допустимих значень нерівності:

а) ; б) ; в) ; г) .

2.               Доведіть, що нерівність не має розв’язків:

а) ;

б) ;

3.               Розв’яжіть нерівність:

а) ;

б) ;

Виконання письмових вправ.

1.               Розв’яжіть нерівність:

а)    д) ;

б) ;   е) .

в) ;   є) ;

г) ;   ж) .

2.               Укажіть найменший цілий розв’язок нерівності:

а) ;

б) ;

3.               Знайдіть середнє арифметичне цілих розв’язків нерівності

.

4.               Знайдіть найменший натуральний розв’язок нерівності

.

6. Підбиття підсумків уроку.

1.               Які способи розв’язування ірраціональних нерівностей ви знаєте?
2.               Поясніть суть медоту інтервалів.
3.               Яким способом розв’язується нерівність виду .
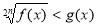4.               В якому випадку нерівність 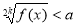не має розв’язку.

7. Домашнє завдання.

Вивчити теоретичний матеріал, з підручника «Бевз Г.П. Алгебра 10клас» №:

587, 592(1,2), 593, 596(2,3), 598.