Ірраціональні рівняння
Тема: Ірраціональні рівняння
Мета: сформувати в учнів уявлення про ірраціональні рівняння; домогтися розуміння та засвоєння учнями алгоритму розв’язування ірраціональних рівнянь шляхом піднесення обох частин рівняння до одного степеня; сформувати вміння розв’язувати ірраціональні рівняння шляхом піднесення обох частин до одного степеня.
Тип уроку: засвоєння знань; формування вмінь.
Наочність та обладнання: конспект уроку «Ірраціональні рівняння», презентація, проектор, таблиця «Ірраціональні рівняння».
І. Організаційний етап.
Перевірка готовності учнів на роботу, налаштування на роботу.
ІІ. Перевірка домашнього завдання.
- Розкрити дужки:
-
Скоротити дріб:
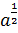 .
.
- Знайти значення виразу:
- 49
- 8
- 81
- 81
ІІІ. Формулювання мети і завдань уроку. Мотивація навчальної діяльності.
Задача. Знайдіть довжини катетів прямокутного трикутника, якщо довжина гіпотенузи дорівнює 25 см, а периметр трикутника — 60 см.
Розв'язання. Нехай довжина одного з катетів дорівнює х см, тоді, за теоремою Піфагора, довжина другого катета дорівнює ![]() см. Оскільки за умовою задачі периметр трикутника дорівнює 60 см, то дістанемо рівняння
см. Оскільки за умовою задачі периметр трикутника дорівнює 60 см, то дістанемо рівняння ![]() .
.
Особливістю цього рівняння є те, що змінна міститься під знаком кореня. Такі рівняння називаються ірраціональними і завдання цього уроку — ознайомитися зі способами розв'язання таких рівнянь.
Ми розглядатимемо розв’язування ірраціональних рівнянь на множині дійсних чисел, тобто розв’язками можуть бути тільки дійсні числа. При цьому під значеннями коренів парного степеня розуміють їх арифметичні значення, тобто вираз під коренем і сам вираз невід’ємні, а під значеннями коренів непарного степеня – їх дійсні значення.
IV. Актуалізація опорних знань.
-
Знайти ОДЗ рівняння: 1)
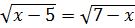 ; 2)
; 2) 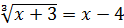
-
Спростити вираз: 1)
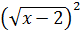 2)
2) 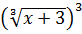
-
Подати у вигляді многочлена: 1)
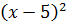 2)
2) 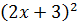
V. Засвоєння знань.
Ірраціональні рівняння
- Рівняння, у яких змінна знаходиться під знаком кореня, називаються ірраціональними рівняннями.
Найчастіше розв’язування ірраціональних рівнянь ґрунтується на зведені заданого рівняння за допомогою деяких перетворень до раціонального рівняння, що рівносильне даному або є його наслідком.
-
Основні способи розв’язання ірраціональних рівнянь:
- за допомогою піднесення обох частин рівняння до одного степеня;
- за допомогою заміни змінних;
- за допомогою застосування властивостей функцій.
- Розв'язування найпростіших ірраціональних рівнянь
Рівняння виду ![]() називаються найпростішими ірраціональними.
називаються найпростішими ірраціональними.
Схема розв'язання найпростіших ірраціональних рівнянь
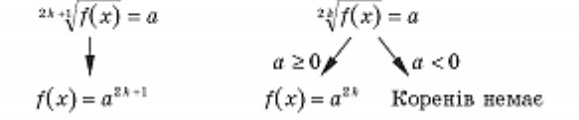
-
Розв’язування ірраціональних рівнянь за допомогою піднесення обох частин до одного степеня
- Якщо обидві частини рівняння піднести до непарного степеня, то отримаємо рівняння, рівносильне даному.
- При піднесенні обох частин рівняння до парного степеня, то отримаємо рівняння-наслідок.
Щоб з’ясувати, чи є одержані числа коренями рівняння, виконують перевірку здобутих розв’язків. Розв’язки, які не задовольняють заданому рівнянню, називають сторонніми коренями для заданого рівняння.
Причина появи стороннього кореня полягає в тому, що застосування формули ![]() призводить до розширення області визначення рівняння.
призводить до розширення області визначення рівняння.
Розв’язати рівняння: ![]() . Підносячи обидві частини до квадрату отримаємо
. Підносячи обидві частини до квадрату отримаємо ![]() або
або ![]() , тобто
, тобто ![]() , Звідси
, Звідси ![]() . Виконаємо перевірку способом підстановки. При х=1 дане рівняння перетворюється на правильну рівність
. Виконаємо перевірку способом підстановки. При х=1 дане рівняння перетворюється на правильну рівність ![]() . Отже х=1 є коренем заданого рівняння. При х=9 дістанемо неправильну рівність
. Отже х=1 є коренем заданого рівняння. При х=9 дістанемо неправильну рівність ![]() ,
,
![]() . Отже х=9 – сторонній корінь.
. Отже х=9 – сторонній корінь.
Спосіб розв’язування ірраціональних рівнянь шляхом піднесення обох частин рівняння до степеня такий, що під час його застосування неможливо втратити корені, але можуть з’явитися сторонні. Тому перевірка здобутих чисел є важливою складовою частиною розв’язування ірраціональних рівнянь.
VІ. Формування вмінь.
- Виконання усних вправ:
- Перевірити, чи є х0 розв’язком рівняння
- Виконання письмових вправ
-
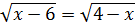
-
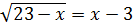
-
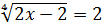
-
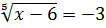
-
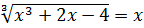
-
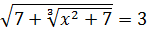
-
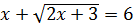
-
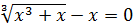 .
.
VІІ. Підсумки уроку






VІІІ. Домашнє завдання
Засвоїти зміст понять, розглянутих на уроці.
§7, ст.. 52, №№ 84, 85(1,2,3,4,5).


про публікацію авторської розробки
Додати розробку
