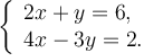Системи лінійних рівнянь з двома змінними.

Тема. Системи лінійних рівнянь з двома змінними. Графічний спосіб

Розв’язування системи лінійних рівнянь з двома змінними.

Мета: сформувати уявлення учнів про розв'язок системи рівнянь із двома змінними та графічний спосіб розв'язання систем лінійних рівнянь; виробити вміння: здійснювати перевірку, чи є пара (х; у) розв'язком даної системи лінійних рівнянь; використовуючи навички побудови графіка лінійного рівняння з двома змінними, розв'язувати систему двох лінійних рівнянь графічним способом.
Тип уроку: засвоєння нових знань.
 

Перевірка домашнього завдання

у формі гри «Знайди помилку»

ДПА-2019 В-4 №18

                                    №1

D= 169,

Тоді ,       

Відповідь: ,    

№2

Визначте графічно кількість розв’язків системи

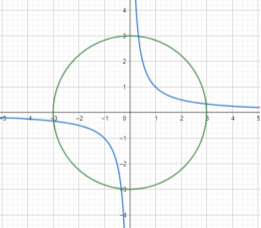
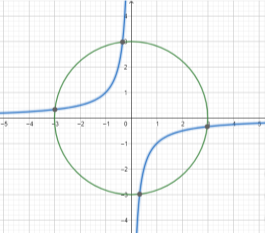
Відповідь: система має 4 розв’язки

                            №3

Розв’яжіть систему рівнянь.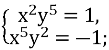

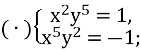
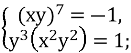
Відповідь:

Актуалізація опорних знань

І. Робота 2х учнів на 2х магнітних дошках

1. пара значень змінних… розв’язком системи рівнянь… з двома змінними… називається … в правильну рівність… яка перетворює кожне рівняння системи (Розв’язком системи рівнянь з двома змінними називається пара значень змінних, яка перетворює кожне рівняння системи в правильну рівність)

2. знайти всі її розв’язки… розв’язати систему рівнянь… або довести, що їх немає… означає.

(Розв’язати систему рівнянь означає знайти всі її розв’язки або довести, що їх немає)

ІІ. Колективна робота

Закінчіть визначення.

Першого учня який відповідатиме на питання обираємо за бажанням, а далі кожен хто відповідатиме називатиме наступного учня, який даватиме відповідь.

1. Два рівняння називаються рівносильними,  якщо всі розв'язки першого рівняння …

(Два рівняння називаються рівносильними,  якщо всі розв'язки першого рівняння є розв'язками другого і, навпаки, всі розв'язки другого рівняння є розв'язками першого).

2. Ми познайомилися з такими методами розв’язування систем рівнянь, як …

(графічний, метод додавання, метод підстановки)

3. Які недоліки графічного методу розв’язування систем рівнянь?

(графічний спосіб не гарантує того, що отриманий результат є точним)

4. Коли графічний метод розв’язування рівнянь є ефективним?

(коли потрібно визначити кількість розв’язків системи або достатньо знайти їх наближено)

5. У чому полягає сутність методу підстановки?

(в заміні даної системи рівнянь рівносильною системою, в якій одне з рівнянь містить тільки одну змінну)

6. Які системи рівнянь можна розв’язати методом додавання?

(систему рівнянь, в якій коефіцієнти при одній і тій самій змінній в обох рівняннях є протилежними числами)

Дякую. Я впевнилася, що ваш попередній досвід дозволить нам рухатися далі

ІІІ. Поясніть як розв’язати систему рівнянь найраціональнішим способом і поясніть суть цього способу

1. Спосіб підстановки

Розв’язання

     Із першого рівняння системи виразимо у через х: у=6-2х. одержаний вираз підставимо в друге рівняння системи:

4х-3(6-2х)=2, звідси 4х-18+6х=2; 10х=20; х=2.

     Одержане значення х підставляємо у вираз у=6-2х;

у=6-2·2.

     Отже, пара (2;2) – розв’язок даної системи.

     Відповідь: (2;2).

     Способом підстановки систему двох рівнянь із двома змінними розв’язують за таким порядком:

1. з одного рівняння системи виражаємо одну зі змінних через другу змінну і відомі величини;

2. знайдене значення підставляємо в друге рівняння системи, одержуємо рівняння відносно другої змінної;

3. розв’язуємо одержане рівняння і знаходимо значення цієї змінної;

4. підставляючи знайдене значення у вираз для першої змінної, одержуємо відповідне її значення;

5. записуємо відповідь.

    Зауваження. Спосіб підстановки, як правило, використовують, якщо коефіцієнт при одній зі змінних в одному з рівнянь системи дорівнює 1.

2. Спосіб додавання

     Розв’язування системи двох лінійних рівнянь із двома змінними способом алгебрагічного додавання виконують за таким порядком:

1) урівнюємо коефіцієнти при одній зі змінних шляхом по членного множення обох рівнянь на множники, підібрані відповідним чином;

2) додаючи (або віднімаючи) почленно рівняння системи, виключаємо одну зі змінних;

3) розв’язуємо одержане рівняння з однією змінною;

4) значення другої змінної можна знайти таким же способом (або підстановкою знайденого значення змінної в будь-яке із заданих рівнянь системи);

5) записуємо відповідь.

    Зауваження. Спосіб додавання, як правило, використовують, якщо коефіцієнти при одній зі змінних у рівнянні системи – протилежні числа.

3. Заміна змінних

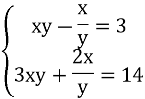
Робота в зошитах

Стратегія «Альпініст» або знайди свою стежину

По членне ділення рівнянь системи

Графічний спосіб

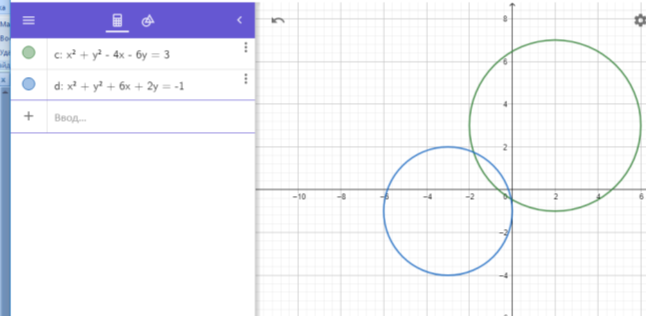
№3

Збірник ДПА-2013 В-32 №4.1

Знайдіть усі значення параметра а, при яких система рівнянь

       має 4 розв’язки.

№4

Збірник ДПА-2013 В-11 №4.1

Знайдіть усі значення параметра а, при яких система має єдиний розв'язок

\