"Ключі до успіху" (Урок, Презентація, Тест)

Про матеріал

Урок з теми "Трикутники". Цікаве узагальнення теми трикутників у курсі геометрія 7 клас.

Мета:

узагальнити та систематизувати знання з теми;

розвивати вміння учнів застосовувати знання з теми до розв'язування ззадач;

розвивати творче та логічне мислення;

підвищувати інтерес до геометрії;

виховувати культуру спілкування.

Тип уроку: узагальнення знань та вміньучнів.

Обладнання: картки з усними задачами, картки з логічними задачами, малюнки для демонстрації, презентація, відео

Зміст архіву

Перегляд файлу

Попередній слайд 1 / 43 Наступний слайд

Зміст слайдів

Номер слайду 1

КЛЮЧІ ДО УСПІХУ

Номер слайду 2

Привітання команд

Номер слайду 3

РОЗМИНКА

Номер слайду 4

СтартІнтерактивна гра. Успех – это определенный результат непрерывной и упорной деятельности, направленной на достижение поставленных целей. Непрерывное обучение – ключ к успеху в ХХI веке. (Писатель Брайан Трейси)Ключі до успіху

Номер слайду 5

Правила гри. Представники команд по черзі вибирають ключі з питаннями на ігровому полі, дають на нього відповідь. Рівень та складність питання закладенна випадковим чином: питання з одним ключом – саме просте, з трьома – найскладніше. Номер питання знаходиться під ключем, на нього потрібно клікнути після того як зникне ключик. За правильну відповідь кожна команда отримує ту кіькість ключів, яке визначене складністю питання. Далі2r

Номер слайду 6

23456789101112151 Знання - наш ключ до успіху!1314 Кінецьrrrrrrrrrrrrrrr

Номер слайду 7

Відповідь. ВМ=АМ як сторони рівнобедреного трикутника1 КлючіКінець

Номер слайду 8

У якому трикутнику висота дорівнює четвертині гіпотенузи. Відповідь. У прямокутному з кутом 1502 КлючіКінець

Номер слайду 9

На які трикутники розбиває медіана довільний трикутник. Відповідь. На рівновеликі3 КлючіКінець

Номер слайду 10

Чи можуть бути два трикутники рівні, якщо в них тільки по два кути рівніВідповідь. Так, якщо ще одна сторона, яка їх сполучає - рівна4 КлючіКінець

Номер слайду 11

Скільки трикутників на рисунку. Відповідьшість5 КлючіКінець

Номер слайду 12

AВС = PQR. R = 28°. Назвати кут трикутника АВС, що дорівнює 28°. ВІдповідьС.6 КлючіКінець

Номер слайду 13

Як довести, що трикутник рівнобедренний. Відповідь. За допомогою зовнішнього кута трикутника, як суміжного7 КлючіКінець

Номер слайду 14

Знайти кути трикутника. Відповідь300 і 6008 КлючіКінець

Номер слайду 15

Відповідь619 КлючіКінець

Номер слайду 16

Відповідь21 см10 КлючіКінець

Номер слайду 17

Знайдіть кути,які утворює висота прямокутного трикутника, проведена до гіпотенузи, з катетами, якщо один з гострих кутів трикутника дорівнює 370 Відповідь 11 Ключі370 та 530 Кінець

Номер слайду 18

Відповідь. На рисунках б) і в)12 КлючіКінець

Номер слайду 19

Один з кутів трикутника у 3 рази більший за другий, а зовнішній кут третього кута дорівнює 280. Знайдіть кути трикутника. Відповідь13 КлючіКінець

Номер слайду 20

Дано ACD = POK. Знайти периметр трикутника ACD, якщо відомо, що PO = 3,4 см, OK = 5,6 см і AD = 7 см. Відповідь. РACD = 17 см14 КлючіКінець

Номер слайду 21

Відповідь. Рівними15 КлючіКінець

Номер слайду 22

Конкурс “Чорний ящик”Завдання. Відповідь

Номер слайду 23

Конкурс “Знаю я і знаєш ти”

Номер слайду 24

Дякую за активність та знання. Ваш ключ до успіху – це ваші знання!

Номер слайду 25

Номер слайду 26

Номер слайду 27

Номер слайду 28

Номер слайду 29

План1. Що таке трикутник?2. Типи трикутниківа) рівнобедренийб)рівносторонннійв)різносторонній3. Класифікація відповідно до їх внутрішніх кутів

Номер слайду 30

Що таке трикутник?— три точки, що не лежать на одній прямій, і три відрізки, що їх сполучають.

Номер слайду 31

Трикутники можна класифікувати в залежності від відносної довжини його сторін: Типи трикутників:

Номер слайду 32

Номер слайду 33

В рівносторонньому трикутнику всі сторони мають однакову довжину. Всі кути рівностороннього трикутника також рівні і дорівнюють 60°. Рівносторонній трикутник ще називають правильним.

Номер слайду 34

Різносторонній трикутник має сторони різної довжини. Внутрішні кути різностороннього трикутника різні.

Номер слайду 35

Класифікація відповідно до їх внутрішніх кутів. Прямокутний трикутник має один внутрішній кут рівний 90° (прямий кут). Сторона, протилежна до прямого кута, називається гіпотенуза. Інші дві сторони називаються катетами прямокутного трикутника. Тупокутний трикутник має один внутрішній кут більший ніж 90°. В гострокутному трикутнику всі кути менші за 90°. Рівносторонній трикутник є гострокутним, але не всі гострокутні трикутники рівносторонні.

Номер слайду 36

Номер слайду 37

Трикутники. Кириленко Анна, 8-б класstyle.font. Size

Номер слайду 38

Що таке трикутник?Трику́тник у евклідовій геометрії — три точки, що не лежать на одній прямій, і три відрізки, що їх сполучають. Трикутник з вершинами A, B, і C позначається ABC. Трикутник є многокутником і 2-симплексом. В евклідовій геометрії трикутник однозначно задає площину. Всі трикутники двовимірні.123style.colorfillcolorstroke.colorfill.typestyle.colorfillcolorstroke.colorfill.typestyle.colorfillcolorstroke.colorfill.typestyle.colorfillcolorstroke.colorfill.typestyle.colorfillcolorstroke.colorfill.typestyle.colorfillcolorstroke.colorfill.typestyle.colorfillcolorstroke.colorfill.typestyle.colorfillcolorstroke.colorfill.typestyle.colorfillcolorstroke.colorfill.type

Номер слайду 39

1. Гостокутний. В гострокутному трикутнику всі кути менші за 90°. Рівносторонній трикутник є гострокутним, але не всі гострокутні трикутники рівносторонні.

Номер слайду 40

2. Тупокутний. Тупокутний трикутник має один внутрішній кут більший ніж 90°.

Номер слайду 41

3. Прямокутний Прямокутний трикутник має один внутрішній кут рівний 90° (прямий кут). Сторона, протилежна до прямого кута, називається гіпотенуза. Інші дві сторони називаються катетами прямокутного трикутника.

Номер слайду 42

Види трикутників за довжиною сторін. В рівносторонньому трикутнику всі сторони мають однакову довжину. Всі кути рівностороннього трикутника також рівні і дорівнюють 60°. Рівносторонній трикутник ще називають правильним. В рівнобедреному трикутнику дві сторони мають однакову довжину, третя сторона при цьому називається основою трикутника. Рівнобедрений трикутник також має однакові кути, які знаходяться при його основі. Різносторонній трикутник має сторони різної довжини. Внутрішні кути різностороннього трикутника різні.рівностороннійрівнобедреннийрізносторонній

Номер слайду 43

Рівнобедренний трикутник. В рівнобедреному трикутнику дві сторони мають однакову довжину, третя сторона при цьому називається основою трикутника. Рівнобедрений трикутник також має однакові кути, які знаходяться при його основі.

Перегляд файлу

Вчитель : Нагорна Антоніна Олександрівна Геометрія 7 –В клас

Тема: Ключі до успіху (Трикутники)

Дата: 27.02.2014 року

Мета:

узагальнити та систематизувати знання з теми;

розвивати вміння учнів застосовувати знання з теми до розв’язування з задач;

розвивати творче та логічне мислення;

підвищувати інтерес до геометрії;

виховувати культуру спілкування.

Тип уроку: узагальнення знань та вмінь учнів.

Додаткове обладнання:

Над шкільною дошкою висить плакат з висловом:

«Міцні знання з теми «Трикутники»» - це один з ключів до успіху у вивченні геометрії

ХІД УРОКУ

Вступне слово вчителя.

Вісім параграфів підручника геометрії 7-го класу знайомлять нас з трикутниками, їх властивостями. Сьогодні на уроці ми узагальнимо і систематизуємо знання про трикутник, повторимо все, що вивчили, і таким чином підготуємося до контрольної роботи.

Урок проведемо у формі гри-пошуку ключів. Команди,а це команда: червоного, зеленого та жовтого трикутника здобуватимуть їх за правильні відповіді.

Команди вітаються одна з одною оголошуючи свої девізи.

Червоний трикутник - Капітан Лаврентій Максим

«Бермудський трикутник»

Девіз: Ми команда бермудський трикутник!

Загадковість – це наш супутник!

Ми команда просто клас!

Всі задачі вирішуємо враз!

Жовтий трикутник – Капітан Бура Іванна

«Ми трикутники веселі,

Ми розумні й мудрі ми.

Ми задачі всі розв’яжем,

І легенькіф і складні

Зелений трикутник – Капітан Потьомкін Лев

З геометричних фігур найпростішою фігурою є трикутник. Яке означення трикутника? (відповідають учні). Вся або майже вся геометрія з часів «Начал» Евкліда спирається на «трьох китах» - трьох ознаках рівності трикутників. Давайте їх пригадаємо (відповідають учні).

А тепер пропоную усні вправи на застосування ознак рівності трикутників.

Конкурс «Розминка для команд»

Прийшов час трохи розім’ятися перед клопіткою працею. Кожна команда має сказати по одному факту, властивості, аксіомі, теоремі що стосуються трикутника. Команди будуть робити це по черзі і не повторюючись. Перемогу оцінюють наступним чином: 1 ключик – команда що перша не змогла пригадати нічого про трикутник; 2-ключики – передостання та 3 ключики - переможці

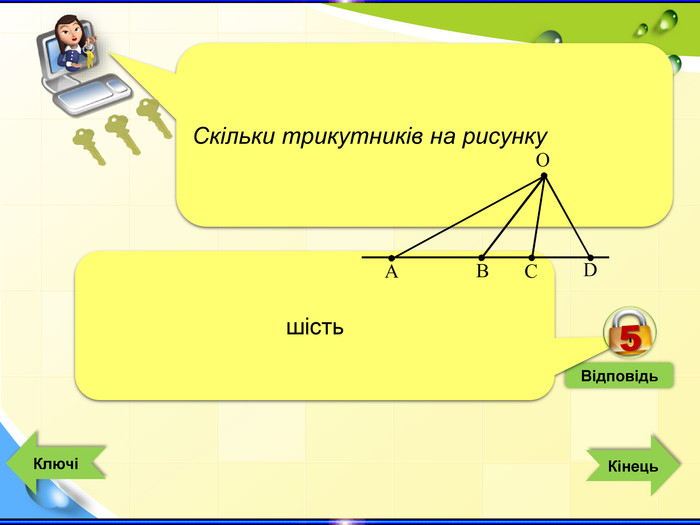
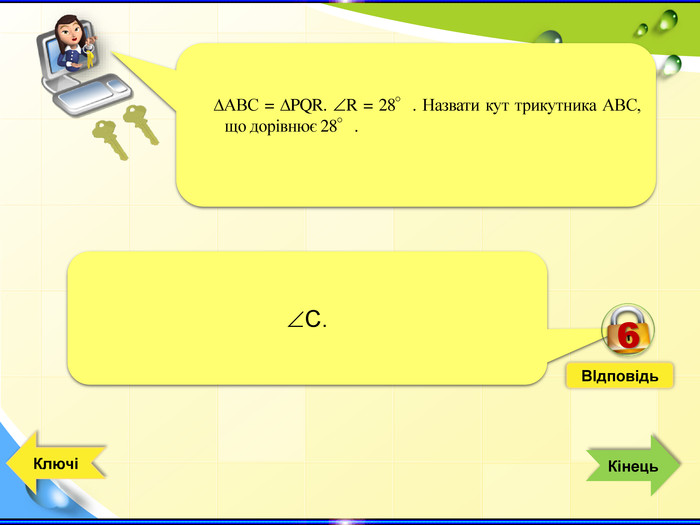
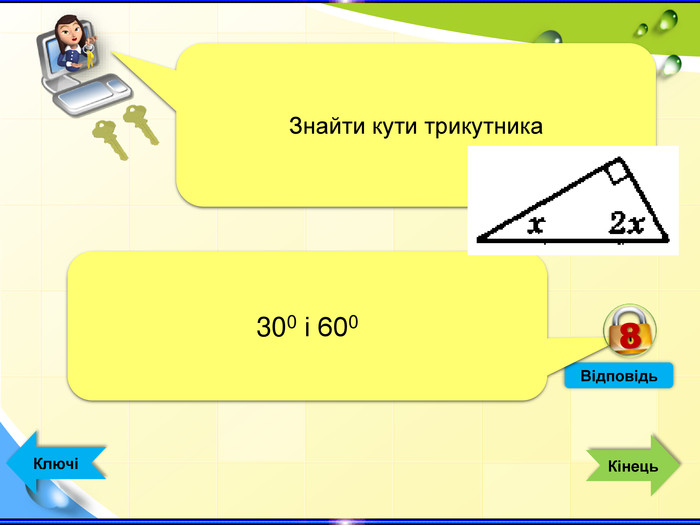
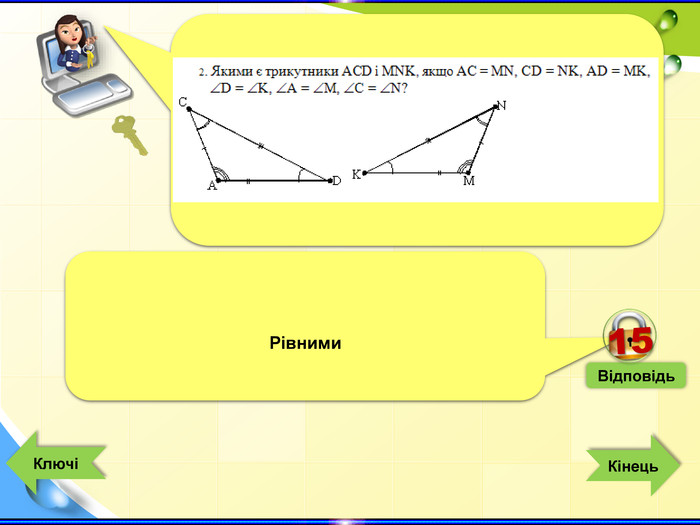
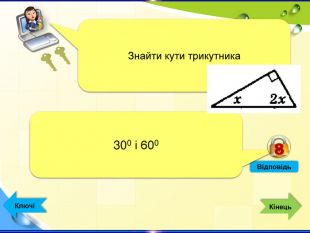
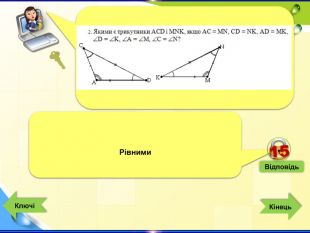
Конкурс «Ключі до успіху» - інтерактивна гра (Додаток 1 презентація «Ключі до успіху»

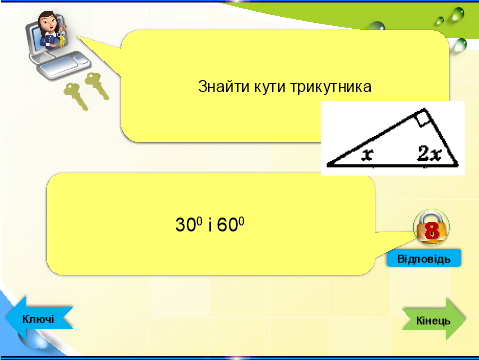
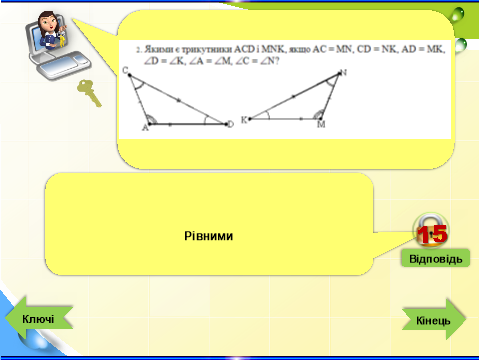
Конкурс «Чорний ящик»

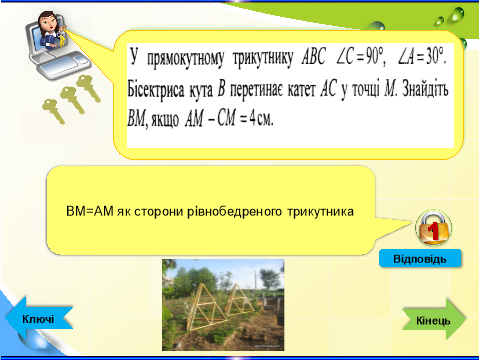
Який кут між бісектрисою і висотою, проведеної з вершини прямого кута, якщо один з гострих кутів 30⁰

^{Перегляд відео у якості відповіді}

Конкурс «Знаю я і знаєш ти»

Командам дається 5 хв для ознайомлення з завданнями. А в цей час бажаючі роблять невелички доповіді про трикутник

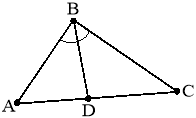
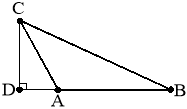
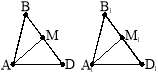
1. (1 бал). Як називається у трикутнику ABC відрізок BD (рис. 1)?

2. (1 бал). Чим є для трикутника ACВ відрізок CD (рис. 2)?

3. (1 бал). Як називається у трикутнику відрізок, що сполучає вершину із серединою протилежної їй сторони?

4. (2 бали). Який із наведених відрізків BM є висотою трикутника ABC?

а) Відрізок BM, що сполучає вершину і точку на протилежній стороні;

б) перпендикуляр BM, проведений із вершини трикутника B до прямої AC;

Рис. 1

Рис. 2

в) відрізок, що сполучає вершину B і точку M — середину сторони AC.

5. (2 бали). Яку з наведених умов прийнято за першу ознаку рівності двох трикутників?

а) Дві сторони одного трикутника дорівнюють відповідно двом сторонам другого трикутника;

б) дві сторони і кут, протилежний одній із цих сторін, одного трикутника дорівнюють відповідно двом сторонам і куту, протилежному одній з цих сторін, другого трикутника;

в) дві сторони і кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними другого трикутника;

г) сторона одного трикутника дорівнює стороні другого трикутника.

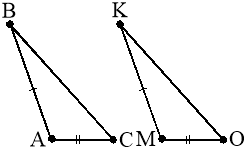
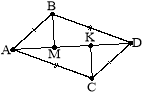
6. (2 бали).Дано трикутники ABC і MKО. Відомо, що AB = MK і AC = MО (рис. 3). При якій з наведених рівностей дані трикутники будуть рівними за третьою ознакою?

а) A = M;

б) C = О;

в) ВC = KО.

Рис. 3

Підсумок уроку.

Вчитель підводить підсумок уроку та оцінює учнів. Відбувається підрахунок ключиків.

Додаткові завдання

(на випадок, якщо учні швидко працюватимуть і залишиться час, то можна їх розпочати і попросити учнів завершити вдома)

Достатній рівень

1. На сторонах OA і OB кута AOB відповідно позначено точки K і Р такі, що KO = PO (рис. 1). Всередині кута взято точку М так, що MK = MP. Довести, що точка M належить бісектрисі кута АОВ.

Дано рівні трикутники ABD і A₁B₁D₁ (рис. 2). На сторонах BD і B₁D₁ позначено відповідно точки M і M₁ такі, що BM = B₁M₁. Довести, що ABM = A₁B₁M₁.
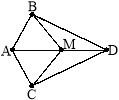
По різні сторони від прямої AD позначено точки B і C такі, що BA = CD і BD = CA (рис. 3). На відрізку AD узято точки M і K, при цьому AM = DK. Довести, що відрізки BM і CK рівні.


Рис. 1	Рис. 2	Рис. 3

Високий рівень

1. По різні сторони від прямої AD позначено точки B і C такі, що промінь AD є бісектрисою кута BAC, а промінь DA є бісектрисою кута BDC (рис. 4). Довести, що будь-яка точка M відрізка AD знаходиться на однаковій відстані від точок B і C.

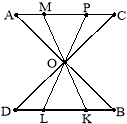
2. На рисунку 5 АOP = BOL. Довести, що COM = DOK.

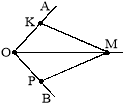
3. На сторонах OM і ON кута MON позначено відповідно точки A і C та B і D такі, що OC = OD і OCB = ODA (рис. 6). Довести, що P — точка перетину відрізків AD і CB — належить бісектрисі кута MON.