Коло і круг. На допомогу вчителю

Геометрія 7 клас «Коло і круг»Педагогічний засіб. Розроблений вчителем математики НВК: ЗОШ І ступеня – гімназії Ямпільського району. Янчук І. В. Янчук І. В.r

Коло і круг. Їх елементи 1.2. Розв’язування вправ 2. Дотична до кола, її властивість2.1. Розв’язування вправ. 3. Коло, описане навколо трикутника 3.1. Розв’язування вправ 4. Коло, вписане в трикутник 4.1. Розв’язування вправ 5. Геометричне місце точок 5.1. Розв’язування вправ Зміст. Янчук І. В.

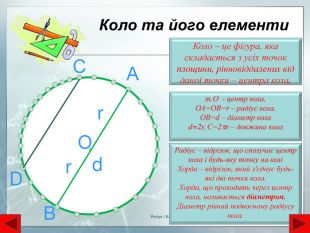
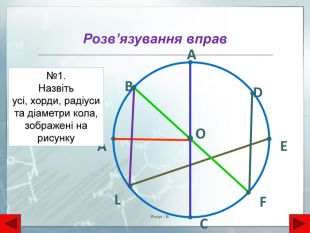
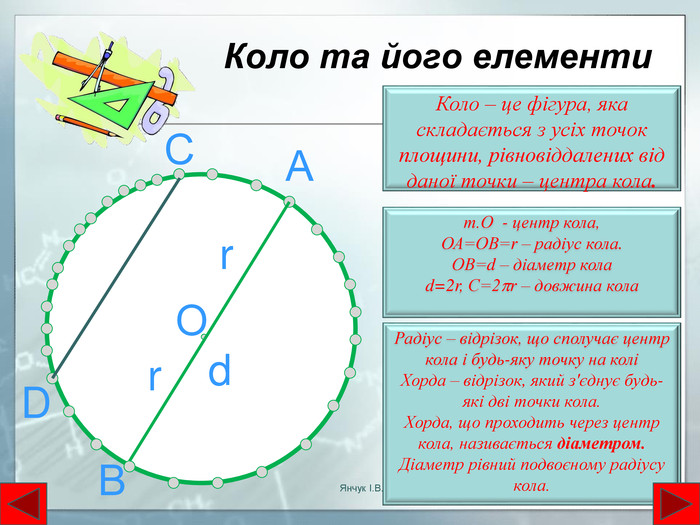
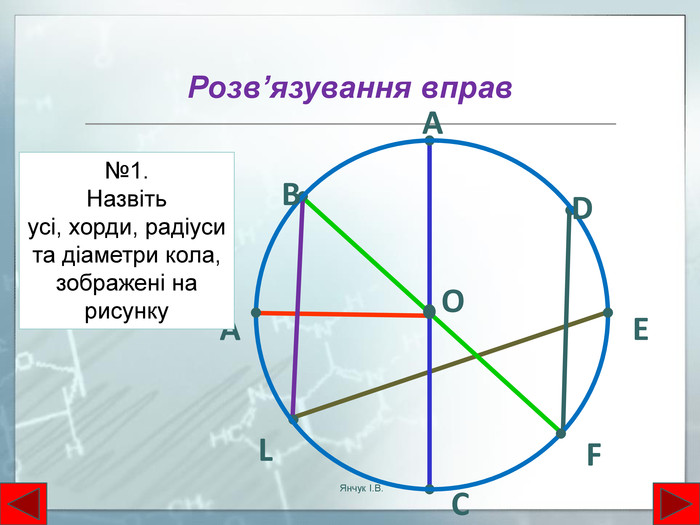
Коло та його елементи. ОКоло – це фігура, яка складається з усіх точок площини, рівновіддалених від даної точки – центра кола. Радіус – відрізок, що сполучає центр кола і будь-яку точку на коліХорда – відрізок, який з'єднує будь-які дві точки кола. Хорда, що проходить через центр кола, називається діаметром. Діаметр рівний подвоєному радіусу кола. Аr. Вd. DСт. О - центр кола, ОА=ОВ=r – радіус кола. ОВ=d – діаметр колаd=2r, С=2r – довжина колаr. Янчук І. В.

Коло будується за допомогою циркуля. Коло і пряма мають дві спільні точки. Пряма називається січною. Коло і пряма мають одну спільну точку. Пряма називається дотичною, точка – точкою дотику. ООЯнчук І. В.style.colorfillcolorstroke.colorfill.type

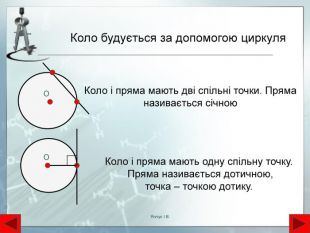
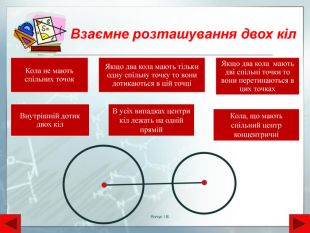
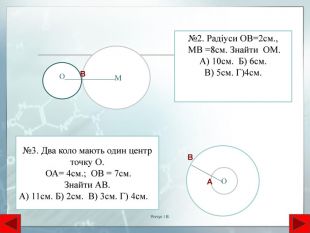
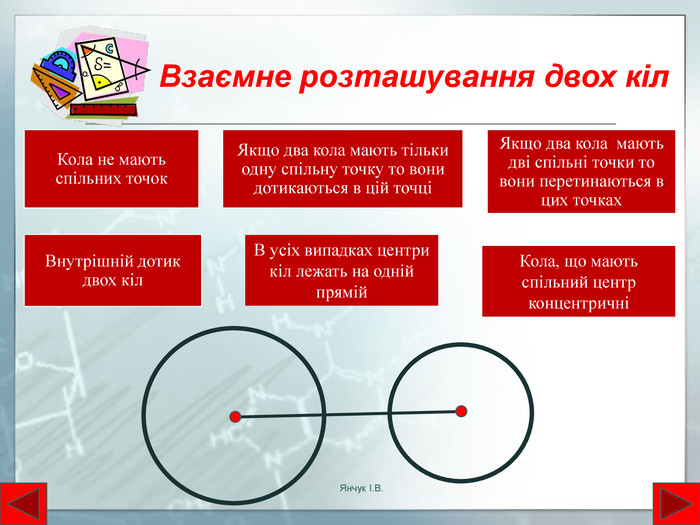
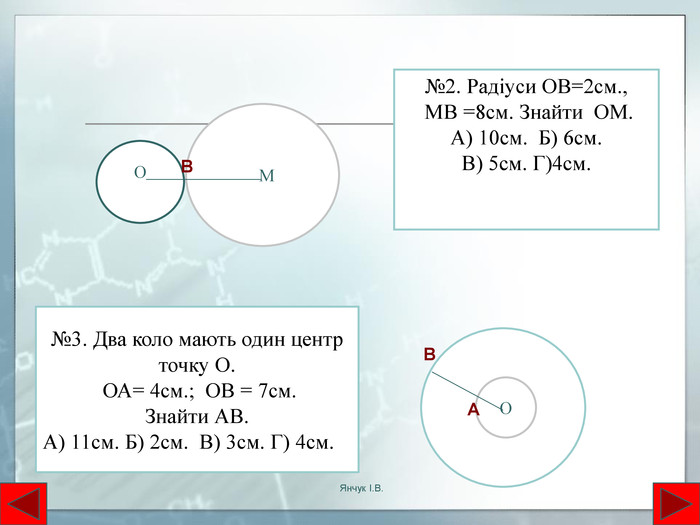
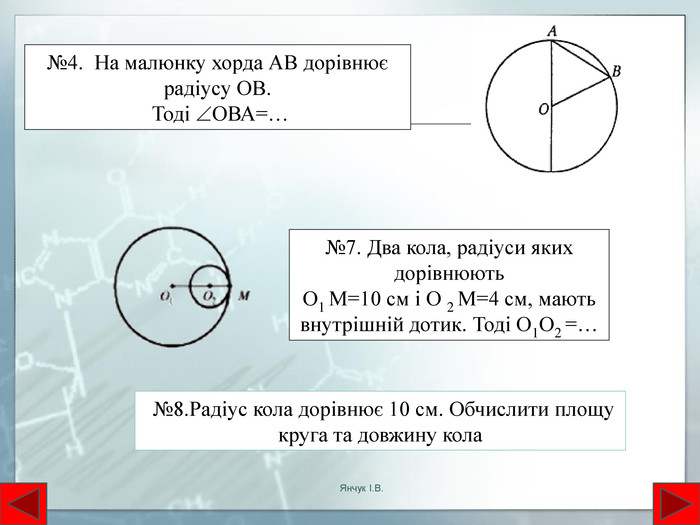
Взаємне розташування двох кіл. Кола не мають спільних точок. Якщо два кола мають дві спільні точки то вони перетинаються в цих точках. Якщо два кола мають тільки одну спільну точку то вони дотикаються в цій точціВнутрішній дотик двох кіл. В усіх випадках центри кіл лежать на одній прямій. Кола, що мають спільний центр концентричніЯнчук І. В.

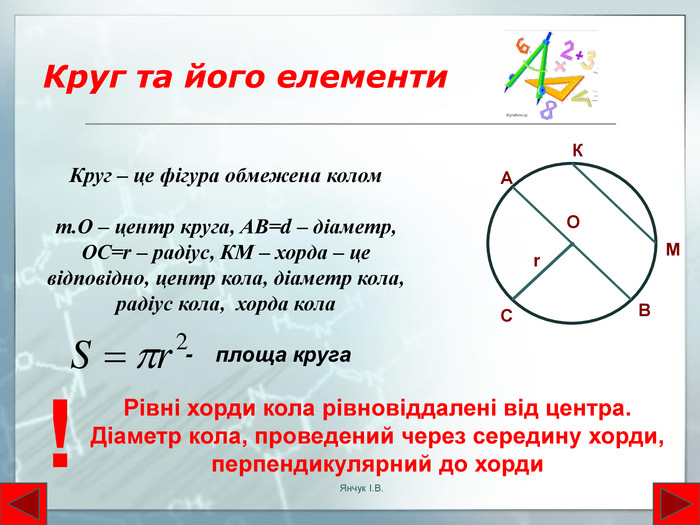
Круг та його елементи. ОВАСr. МККруг – це фігура обмежена коломт. О – центр круга, АВ=d – діаметр, ОС=r – радіус, КМ – хорда – це відповідно, центр кола, діаметр кола, радіус кола, хорда кола - площа круга. Рівні хорди кола рівновіддалені від центра. Діаметр кола, проведений через середину хорди, перпендикулярний до хорди!Янчук І. В.

АВDEFLOРозв’язування вправ№1. Назвіть усі, хорди, радіуси та діаметри кола, зображені на рисунку. САЯнчук І. В.

№2. Радіуси ОВ=2см., МВ =8см. Знайти ОМ. А) 10см. Б) 6см. В) 5см. Г)4см. О М№3. Два коло мають один центр точку О. ОА= 4см.; ОВ = 7см. Знайти АВ. А) 11см. Б) 2см. В) 3см. Г) 4см. ООВВАЯнчук І. В.

№4. На малюнку хорда АВ дорівнює радіусу ОВ. Тоді ОВА=… №7. Два кола, радіуси яких дорівнюють О1 М=10 см і О 2 М=4 см, мають внутрішній дотик. Тоді О1 О2 =… №8. Радіус кола дорівнює 10 см. Обчислити площу круга та довжину кола. Янчук І. В.

№9. Відрізок, зображений на малюнку називається…. А) радіусом; Б) хордою; В)діаметром; Г) інша відповідь. №10. Радіус кола дорівнює 7 см. Тоді його діаметр дорівнює: А) 3,5 см; Б) 7 см; В) 14 см; Г) інша відповідь. Перейдіть у програму DG, натиснувши на смайлик. В програмі виконайте такі завдання: Побудувати коло та провести радіус, діаметр хорду. Побудувати різні варіанти взаємного розміщення кіл. Янчук І. В.

Дотична до кола та її властивість Якщо пряма і коло мають одну спільну точку, то пряма називається дотичною, а точка називається точкою дотику. ОАат. А – точка дотику, пряма а – дотична Янчук І. В.

Властивості дотичної до кола 1. Дотична до кола перпендикулярна до його радіуса проведеного в точку дотику. ОА  а. ОАа2. Точки дотику кола до сторін кута рівновіддалені від його вершини. АВ = АСАОВСЯнчук І. В.

Розв’язування вправ№2. Пряма АВ – є дотичною до кола, радіус якого ОВ. Маємо ВОС=120°. Визначити АВС. DC — дотична до кола. Кут ВАС дорівнює 20°. Обчис­літь кути трикутника ОАВ (рис. 122). №1. DC — дотична до кола. Кут ВАС дорівнює 20°. Обчисліть кути трикутника ОАВЯнчук І. В.

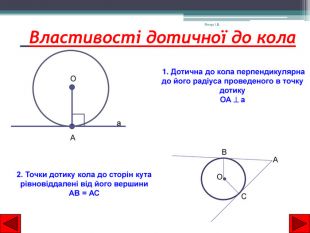
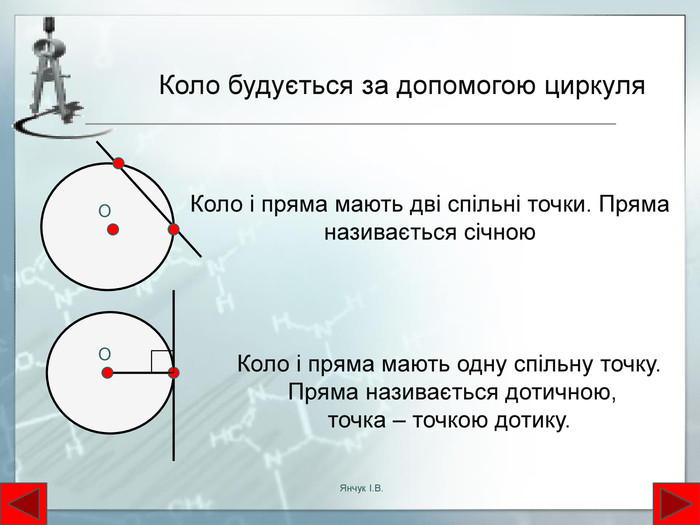
№4. Дотична до кола зображена на малюнку…ГВБАНакресліть коло з центром в точці О і радіусом 3 одиниці.2. Проведіть у даному колі радіус, діаметр і хорду, що не є діаметром. Якому з цих відрізків не належить центр кола?3. Виділіть на рисунку іншим кольором відрізок за­ вдовжки 6 одиниці.4. Позначте всередині кола точку, яка не збігається з точкою О.  Скільки радіусів, діаметрів, хорд можна провести через позначену точку?Знайдіть помилку в зображенні дотичної АВ до даного кола (рис. 124). №3. Знайдіть помилку в зображенні дотичної АВ до даного кола. Натисніть на сонечко та перейдіть у програму DG, де виконайте такі завдання. Янчук І. В.

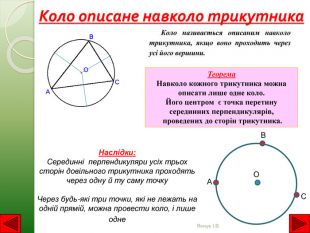
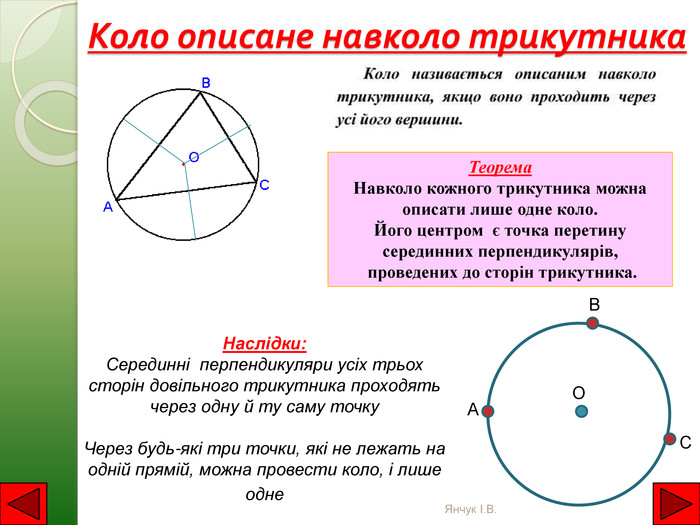
Коло описане навколо трикутника. Теорема Навколо кожного трикутника можна описати лише одне коло. Його центром є точка перетину серединних перпендикулярів, проведених до сторін трикутника. Наслідки: Серединні перпендикуляри усіх трьох сторін довільного трикутника проходять через одну й ту саму точку. Через будь-які три точки, які не лежать на одній прямій, можна провести коло, і лише одне. ОСВАЯнчук І. В.

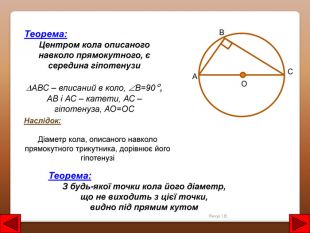
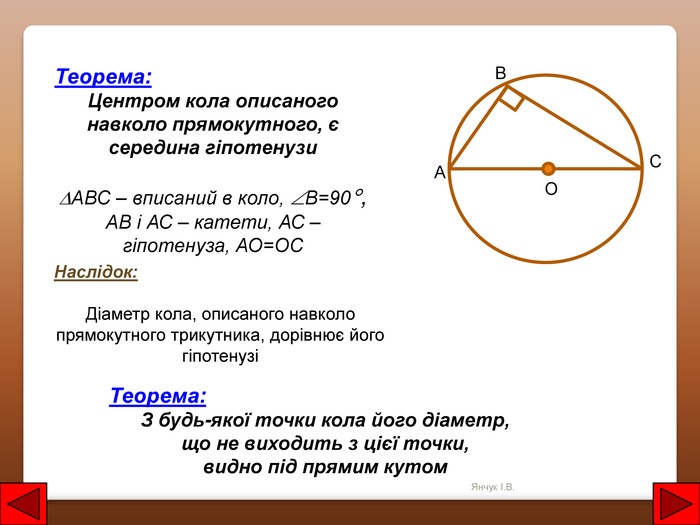
Теорема: З будь-якої точки кола його діаметр, що не виходить з цієї точки, видно під прямим кутом. ОСВАНаслідок: Діаметр кола, описаного навколо прямокутного трикутника, дорівнює його гіпотенузіТеорема: Центром кола описаного навколо прямокутного, є середина гіпотенузиАВС – вписаний в коло, В=90, АВ і АС – катети, АС – гіпотенуза, АО=ОСЯнчук І. В.

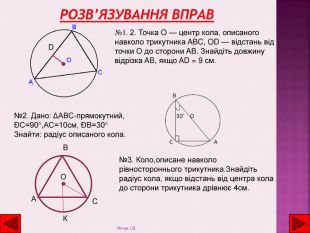
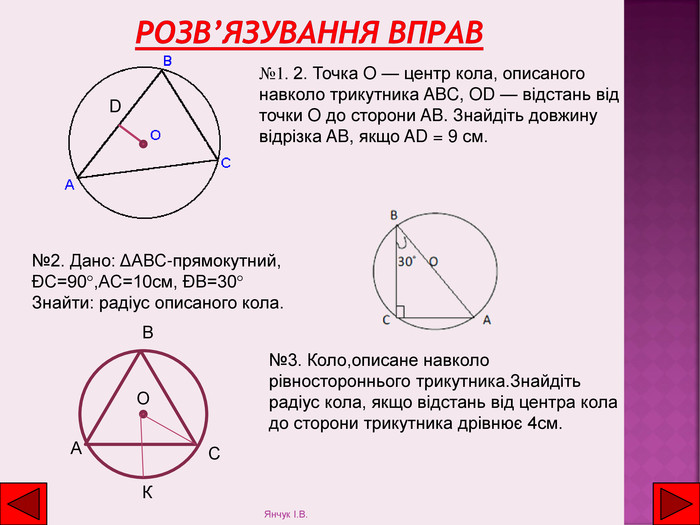
Розв’язування вправ№1. 2. Точка O — центр кола, описаного навколо трикутника ABC, OD — відстань від точки O до сторони AB. Знайдіть довжину відрізка AB, якщо AD = 9 см. D№2. Дано: ΔАВС-прямокутний,ÐС=90°,АС=10см, ÐВ=30°Знайти: радіус описаного кола.№3. Коло,описане навколо рівностороннього трикутника. Знайдіть радіус кола, якщо відстань від центра кола до сторони трикутника дрівнює 4см. ОСВАКЯнчук І. В.

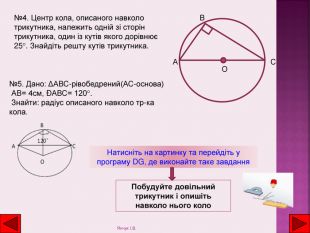
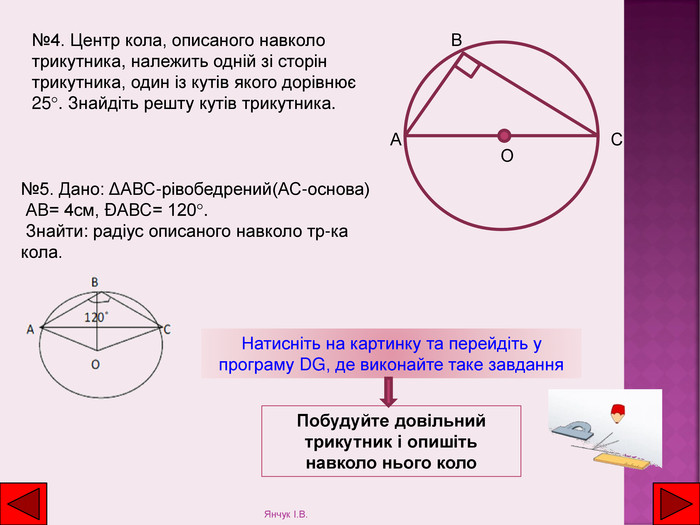
Натисніть на картинку та перейдіть у програму DG, де виконайте таке завдання. Побудуйте довільний трикутник і опишіть навколо нього коло№4. Центр кола, описаного навколо трикутника, належить одній зі сторінтрикутника, один із кутів якого дорівнює 25°. Знайдіть решту кутів трикутника. ОВА№5. Дано: ΔАВС-рівобедрений(АС-основа) АВ= 4см, ÐАВС= 120°. Знайти: радіус описаного навколо тр-ка кола. СЯнчук І. В.

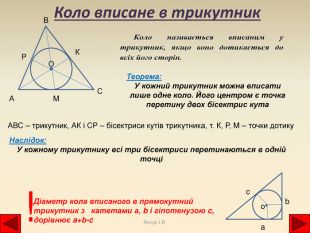
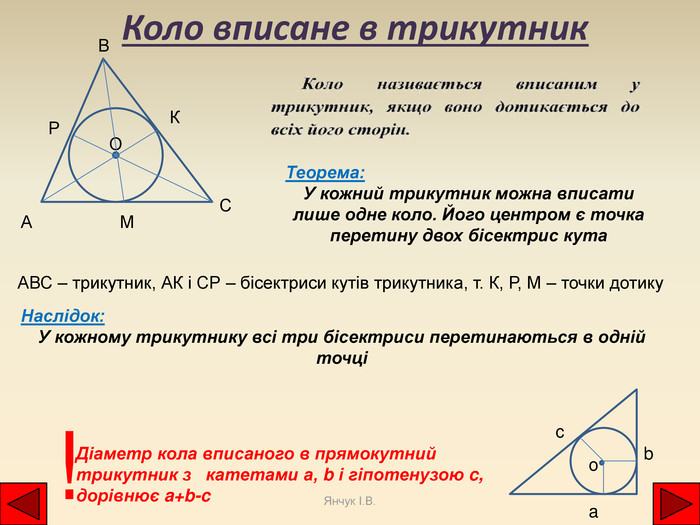
Коло вписане в трикутник. ОСВАРМКТеорема: У кожний трикутник можна вписати лише одне коло. Його центром є точка перетину двох бісектрис кута АВС – трикутник, АК і СР – бісектриси кутів трикутника, т. К, Р, М – точки дотику. Наслідок: У кожному трикутнику всі три бісектриси перетинаються в одній точціДіаметр кола вписаного в прямокутний трикутник з катетами а, b і гіпотенузою c, дорівнює a+b-c!cbao. Янчук І. В.

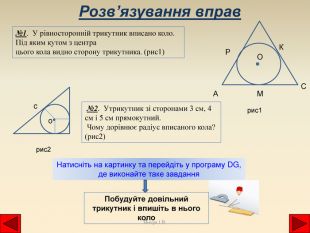
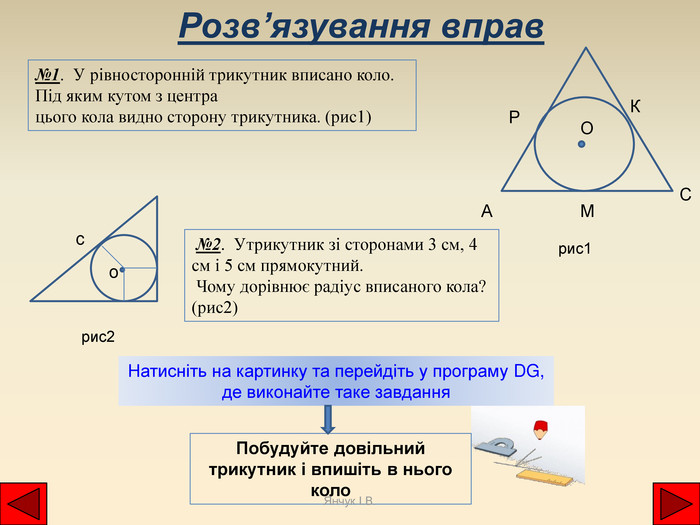
№1. У рівносторонній трикутник вписано коло. Під яким кутом з центра цього кола видно сторону трикутника. (рис1)Розв’язування вправ. ОСАРМК №2. Утрикутник зі сторонами 3 см, 4 см і 5 см прямокутний. Чому дорівнює радіус вписаного кола? (рис2)coрис1рис2 Натисніть на картинку та перейдіть у програму DG, де виконайте таке завдання. Побудуйте довільний трикутник і впишіть в нього коло. Янчук І. В.

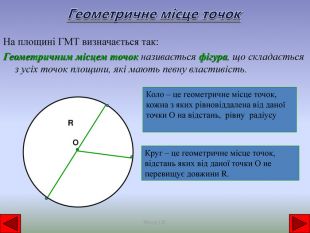
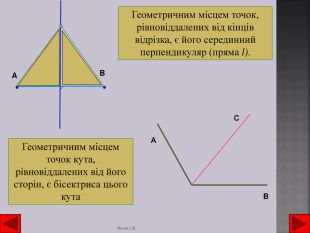
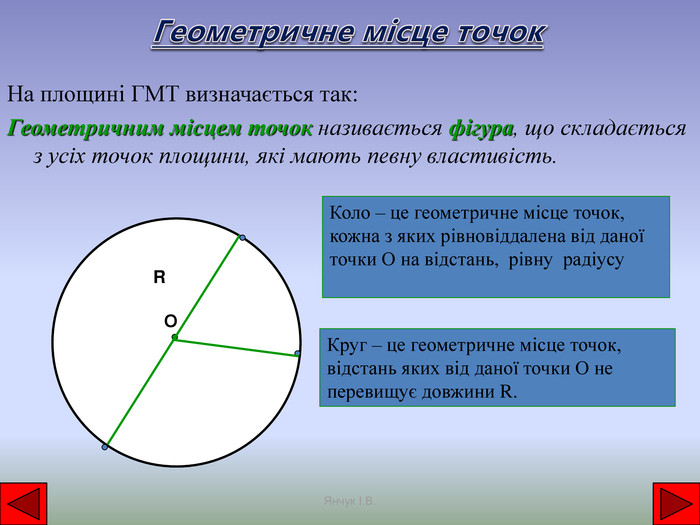
Геометричне місце точок На площині ГМТ визначається так: Геометричним місцем точок називається фігура, що складається з усіх точок площини, які мають певну властивість. Коло – це геометричне місце точок, кожна з яких рівновіддалена від даної точки О на відстань, рівну радіусу. Круг – це геометричне місце точок, відстань яких від даної точки О не перевищує довжини R. ОRЯнчук І. В.r

Геометричним місцем точок, рівновіддалених від кінців відрізка, є його серединний перпендикуляр (пряма l). ABCГеометричним місцем точок кута, рівновіддалених від його сторін, є бісектриса цього кута АBСЯнчук І. В.

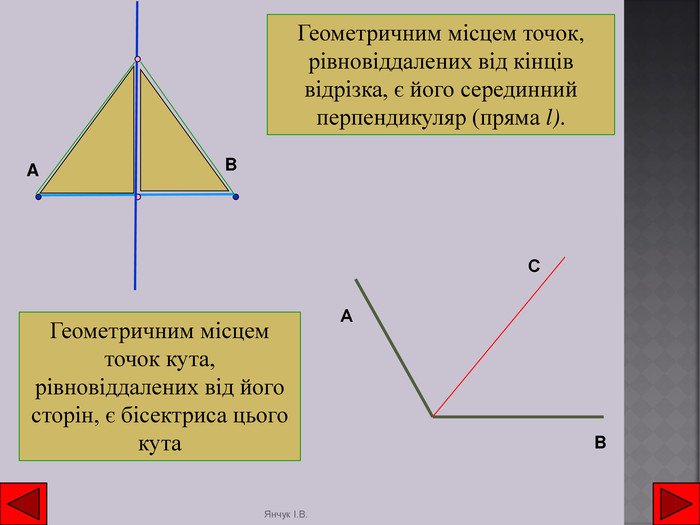
№1. Чи можна вважати круг радіуса 5 см геометричним місцем точок, що віддалені від центра цього круга на відстань, яка:а) дорівнює 5 см; б) не більше 5 см;в) не менше 5 см; г) не більша 4 см?№2. Точки А, В і С не лежать на одній прямій. Побудуйте точку, рівновіддалену від точок А, В і С.№3. Побудуйте точку, рівновіддалену від сторін даного кута, що лежить на відстані а від його вершини. Розв’язування вправ1. Накресліть трикутник ABC.а) Побудуйте геометричне місце точок, рівновіддалених від вершин A і B.б) Побудуйте геометричне місце точок, рівновіддалених від сторін AC і AB.в) Позначте точку перетину побудованих геометричних місць і опишіть її властивості. Натисніть на картинку та перейдіть у програму DG, де виконайте таке завдання. Янчук І. В.