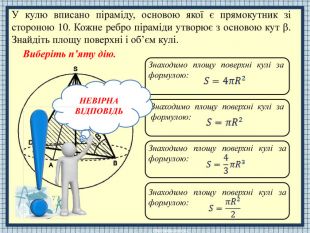
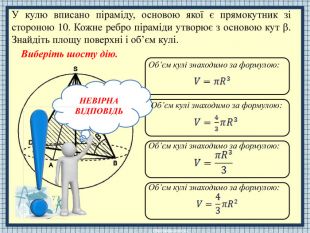
Презентація до уроку зі стереометрії

ЗАДАЧА-МЕТОДСТЕРЕОМЕТРІЯ

До запропонованої задачі встановити вірну послідовність дій її розв’язку.ІНСТРУКЦІЯ

ЗАДАЧА №1 Основою піраміди є паралелограм зі сторонами 9 і 10, одна з його діагоналей дорівнює 11. Протилежні бічні ребра піраміди рівні і кожне з більших дорівнює 10,5. Знайдіть об’єм піраміди. APODCB

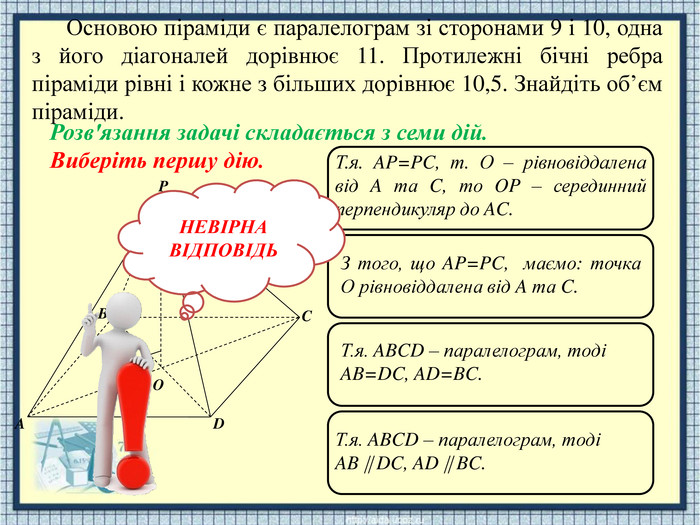
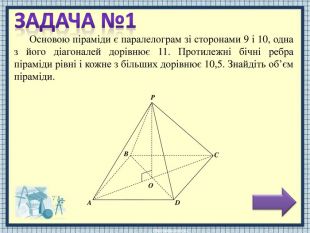
APODCBТ.я. AP=PC, т. О – рівновіддалена від A та C, то OP – серединний перпендикуляр до AC. З того, що AP=PC, маємо: точка О рівновіддалена від A та C. Т.я. ABCD – паралелограм, тоді AB=DC, AD=BC. Т.я. ABCD – паралелограм, тоді AB  DC, AD  BC. НЕВІРНАВІДПОВІДЬОсновою піраміди є паралелограм зі сторонами 9 і 10, одна з його діагоналей дорівнює 11. Протилежні бічні ребра піраміди рівні і кожне з більших дорівнює 10,5. Знайдіть об’єм піраміди. Розв'язання задачі складається з семи дій. Виберіть першу дію.

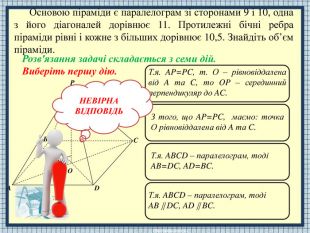
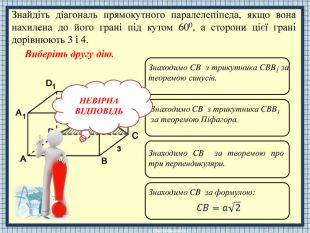
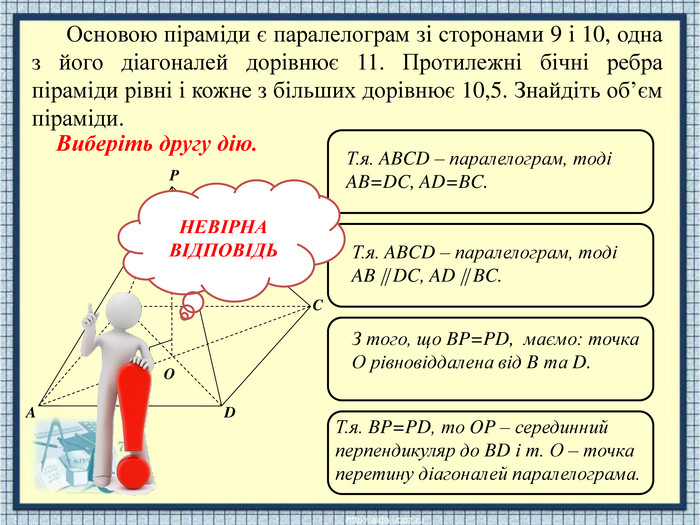
APODCBТ.я. ABCD – паралелограм, тоді AB=DC, AD=BC. Т.я. ABCD – паралелограм, тоді AB  DC, AD  BC. З того, що BP=PD, маємо: точка О рівновіддалена від B та D. Т.я. BP=PD, то OP – серединний перпендикуляр до BD і т. О – точка перетину діагоналей паралелограма. НЕВІРНАВІДПОВІДЬОсновою піраміди є паралелограм зі сторонами 9 і 10, одна з його діагоналей дорівнює 11. Протилежні бічні ребра піраміди рівні і кожне з більших дорівнює 10,5. Знайдіть об’єм піраміди. Виберіть другу дію.

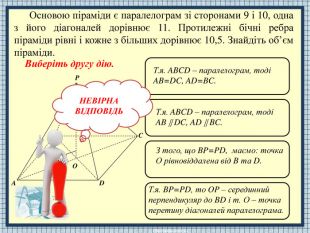
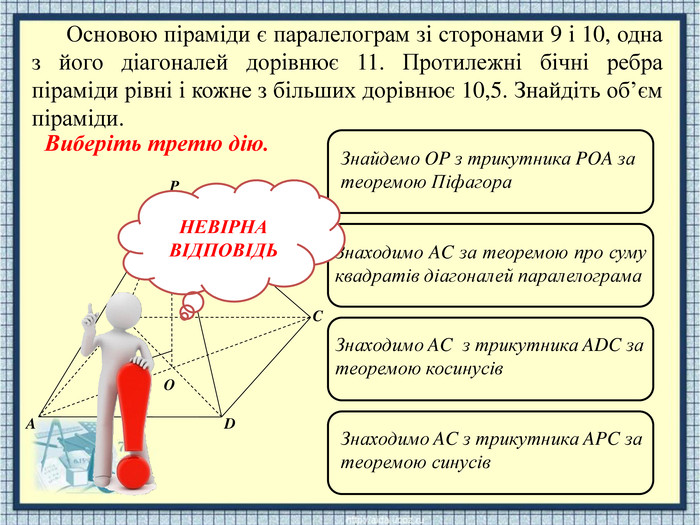
APODCBЗнайдемо OP з трикутника POA за теоремою Піфагора. Знаходимо AC за теоремою про суму квадратів діагоналей паралелограма. Знаходимо AC з трикутника ADC за теоремою косинусів. Знаходимо AC з трикутника APC за теоремою синусів. НЕВІРНАВІДПОВІДЬОсновою піраміди є паралелограм зі сторонами 9 і 10, одна з його діагоналей дорівнює 11. Протилежні бічні ребра піраміди рівні і кожне з більших дорівнює 10,5. Знайдіть об’єм піраміди. Виберіть третю дію.

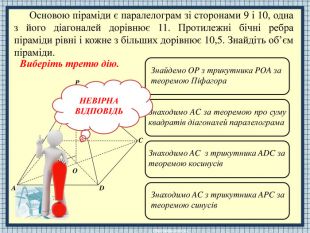
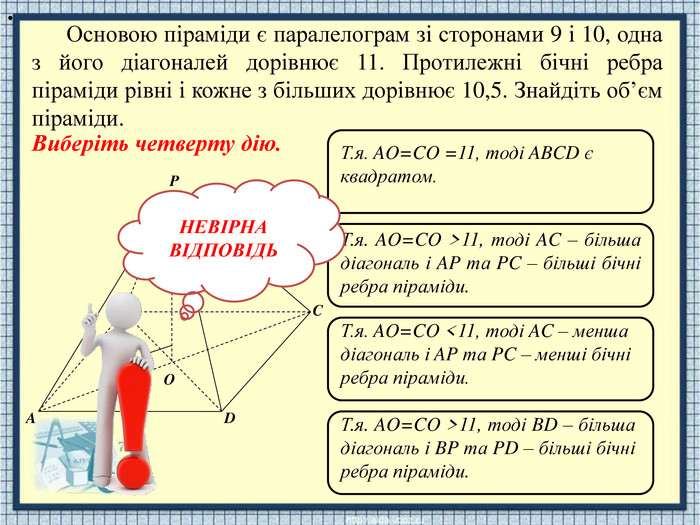
APODCBТ.я. AO=CO =11, тоді ABCD є квадратом. Т.я. AO=CO >11, тоді AC – більша діагональ і AP та PC – більші бічні ребра піраміди. Т.я. AO=CO <11, тоді AC – менша діагональ і AP та PC – менші бічні ребра піраміди. Т.я. AO=CO >11, тоді BD – більша діагональ і BP та PD – більші бічні ребра піраміди. НЕВІРНАВІДПОВІДЬОсновою піраміди є паралелограм зі сторонами 9 і 10, одна з його діагоналей дорівнює 11. Протилежні бічні ребра піраміди рівні і кожне з більших дорівнює 10,5. Знайдіть об’єм піраміди. Виберіть четверту дію.

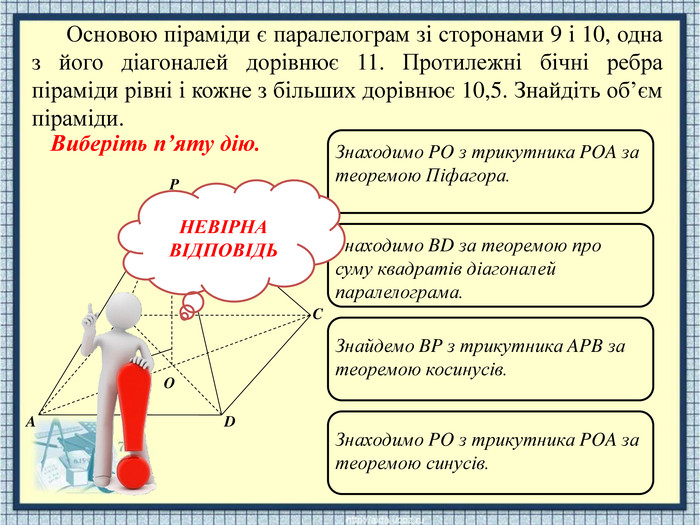
APODCBЗнаходимо PO з трикутника POA за теоремою Піфагора. Знаходимо BD за теоремою про суму квадратів діагоналей паралелограма. Знайдемо BP з трикутника APB за теоремою косинусів. Знаходимо PO з трикутника POA за теоремою синусів. НЕВІРНАВІДПОВІДЬОсновою піраміди є паралелограм зі сторонами 9 і 10, одна з його діагоналей дорівнює 11. Протилежні бічні ребра піраміди рівні і кожне з більших дорівнює 10,5. Знайдіть об’єм піраміди. Виберіть п’яту дію.

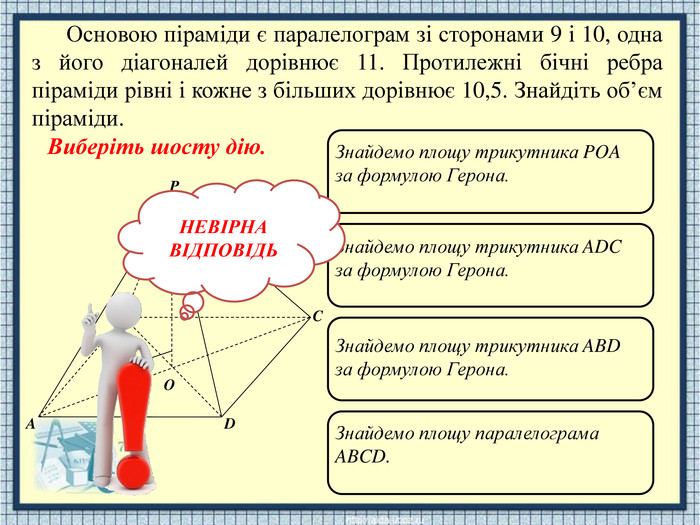
APODCBЗнайдемо площу трикутника POA за формулою Герона. Знайдемо площу трикутника ADC за формулою Герона. Знайдемо площу трикутника ABD за формулою Герона. Знайдемо площу паралелограма ABCD. НЕВІРНАВІДПОВІДЬОсновою піраміди є паралелограм зі сторонами 9 і 10, одна з його діагоналей дорівнює 11. Протилежні бічні ребра піраміди рівні і кожне з більших дорівнює 10,5. Знайдіть об’єм піраміди. Виберіть шосту дію.

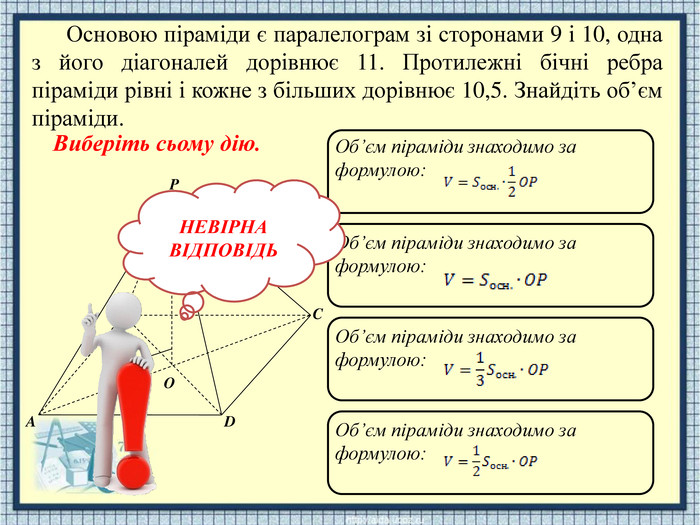
APODCBОб’єм піраміди знаходимо за формулою: Об’єм піраміди знаходимо за формулою: Об’єм піраміди знаходимо за формулою: Об’єм піраміди знаходимо за формулою: НЕВІРНАВІДПОВІДЬОсновою піраміди є паралелограм зі сторонами 9 і 10, одна з його діагоналей дорівнює 11. Протилежні бічні ребра піраміди рівні і кожне з більших дорівнює 10,5. Знайдіть об’єм піраміди. Виберіть сьому дію.

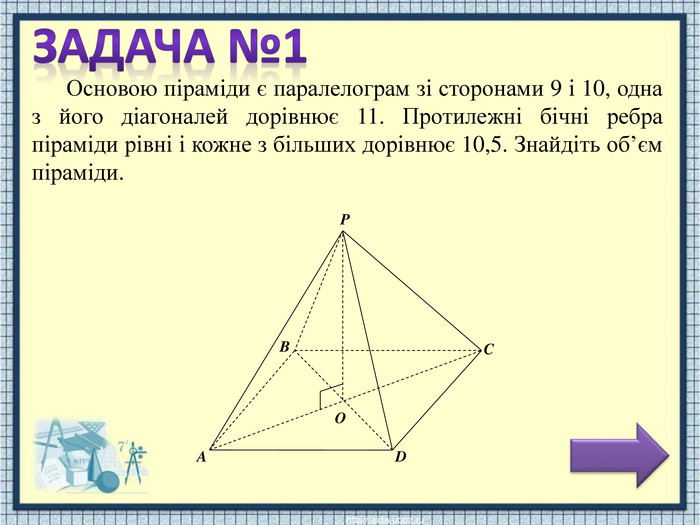
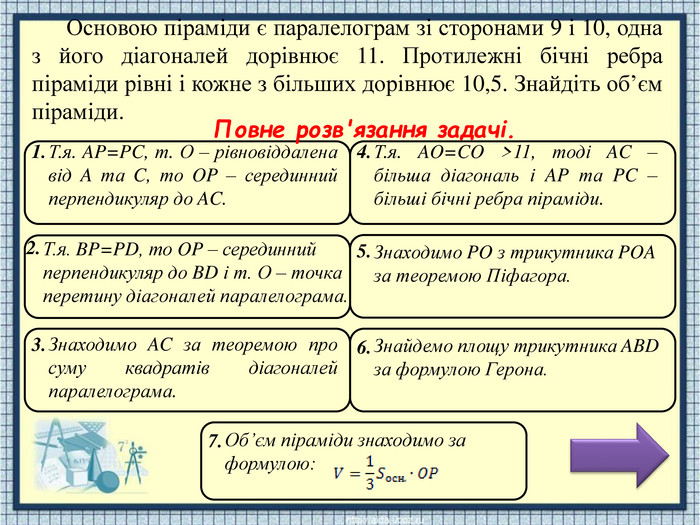
1.2.3.4.5.6.7. Основою піраміди є паралелограм зі сторонами 9 і 10, одна з його діагоналей дорівнює 11. Протилежні бічні ребра піраміди рівні і кожне з більших дорівнює 10,5. Знайдіть об’єм піраміди. Т.я. AP=PC, т. О – рівновіддалена від A та C, то OP – серединний перпендикуляр до AC. Т.я. BP=PD, то OP – серединний перпендикуляр до BD і т. О – точка перетину діагоналей паралелограма. Знаходимо AC за теоремою про суму квадратів діагоналей паралелограма. Т.я. AO=CO >11, тоді AC – більша діагональ і AP та PC – більші бічні ребра піраміди. Знаходимо PO з трикутника POA за теоремою Піфагора. Знайдемо площу трикутника ABD за формулою Герона. Об’єм піраміди знаходимо за формулою: Повне розв'язання задачі.

ЗАДАЧА №2 У кулю вписано піраміду, основою якої є прямокутник зі стороною 10. Кожне ребро піраміди утворює з основою кут . Знайдіть площу поверхні і об’єм кулі.

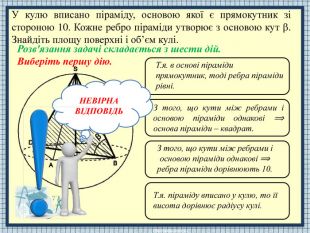
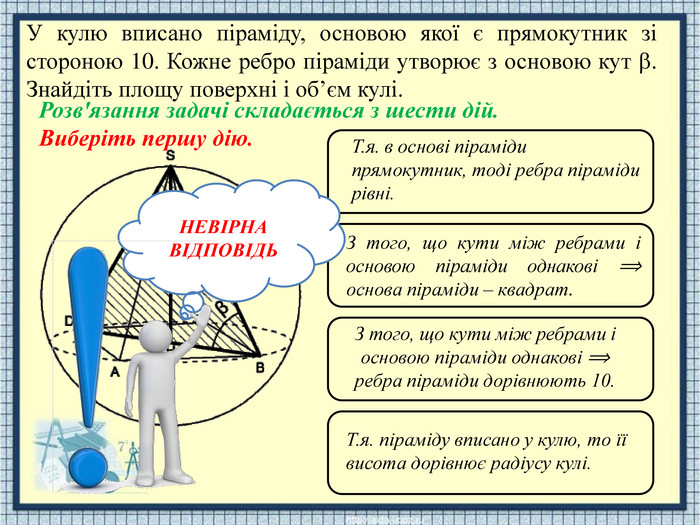
Т.я. в основі піраміди прямокутник, тоді ребра піраміди рівні. З того, що кути між ребрами і основою піраміди однакові ⟹ основа піраміди – квадрат. З того, що кути між ребрами і основою піраміди однакові ⟹ ребра піраміди дорівнюють 10. Т.я. піраміду вписано у кулю, то її висота дорівнює радіусу кулі.. НЕВІРНАВІДПОВІДЬУ кулю вписано піраміду, основою якої є прямокутник зі стороною 10. Кожне ребро піраміди утворює з основою кут . Знайдіть площу поверхні і об’єм кулі. Розв'язання задачі складається з шести дій. Виберіть першу дію.

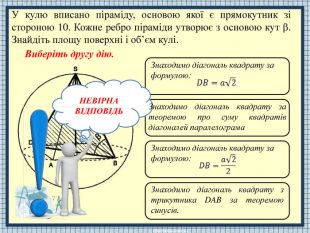
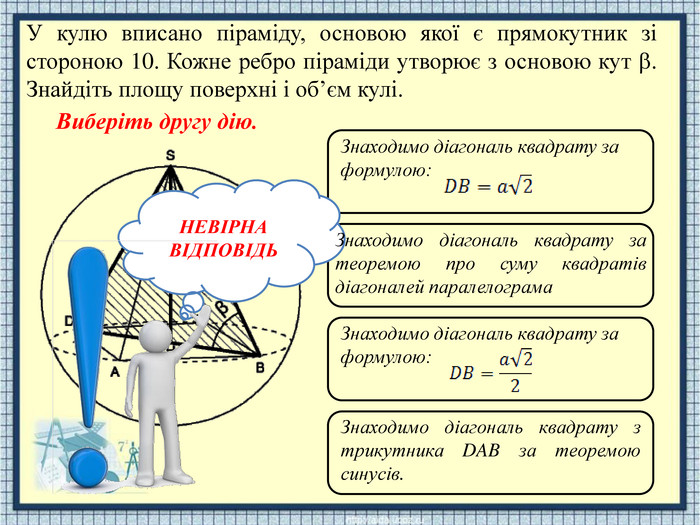
НЕВІРНАВІДПОВІДЬЗнаходимо діагональ квадрату за формулою: Знаходимо діагональ квадрату за формулою: Знаходимо діагональ квадрату з трикутника DAB за теоремою синусів. Знаходимо діагональ квадрату за теоремою про суму квадратів діагоналей паралелограма. У кулю вписано піраміду, основою якої є прямокутник зі стороною 10. Кожне ребро піраміди утворює з основою кут . Знайдіть площу поверхні і об’єм кулі. Виберіть другу дію.

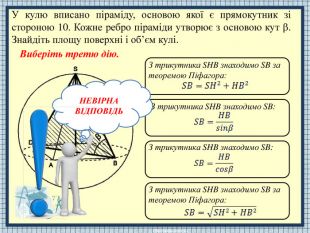
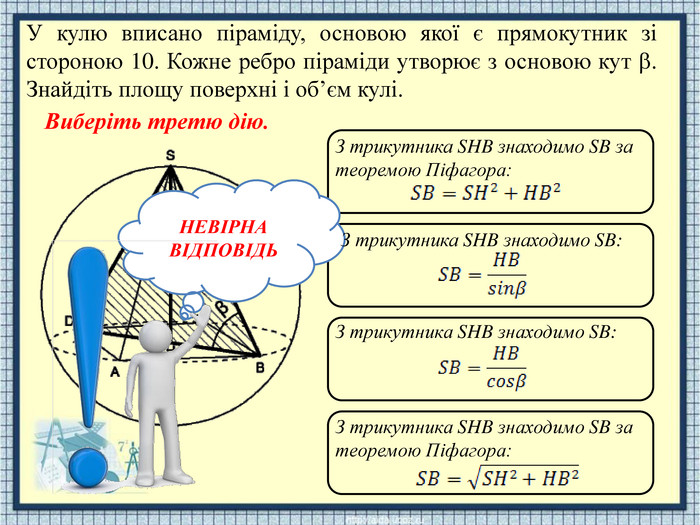
НЕВІРНАВІДПОВІДЬЗ трикутника SHB знаходимо SB: З трикутника SHB знаходимо SB за теоремою Піфагора: З трикутника SHB знаходимо SB: З трикутника SHB знаходимо SB за теоремою Піфагора: У кулю вписано піраміду, основою якої є прямокутник зі стороною 10. Кожне ребро піраміди утворює з основою кут . Знайдіть площу поверхні і об’єм кулі. Виберіть третю дію.

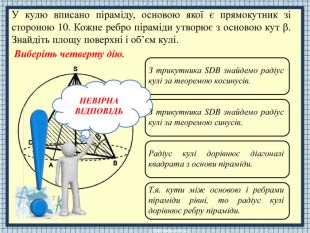
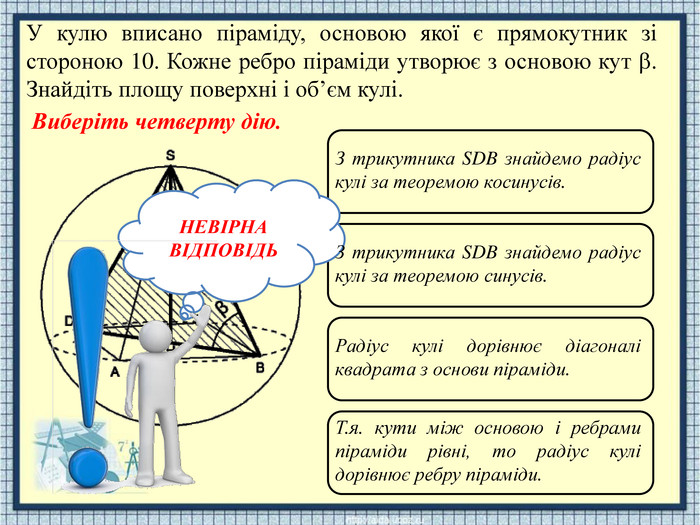
НЕВІРНАВІДПОВІДЬЗ трикутника SDB знайдемо радіус кулі за теоремою косинусів. Т.я. кути між основою і ребрами піраміди рівні, то радіус кулі дорівнює ребру піраміди. З трикутника SDB знайдемо радіус кулі за теоремою синусів. Радіус кулі дорівнює діагоналі квадрата з основи піраміди. У кулю вписано піраміду, основою якої є прямокутник зі стороною 10. Кожне ребро піраміди утворює з основою кут . Знайдіть площу поверхні і об’єм кулі. Виберіть четверту дію.

НЕВІРНАВІДПОВІДЬЗнаходимо площу поверхні кулі за формулою: Знаходимо площу поверхні кулі за формулою: Знаходимо площу поверхні кулі за формулою: Знаходимо площу поверхні кулі за формулою: У кулю вписано піраміду, основою якої є прямокутник зі стороною 10. Кожне ребро піраміди утворює з основою кут . Знайдіть площу поверхні і об’єм кулі. Виберіть п’яту дію.

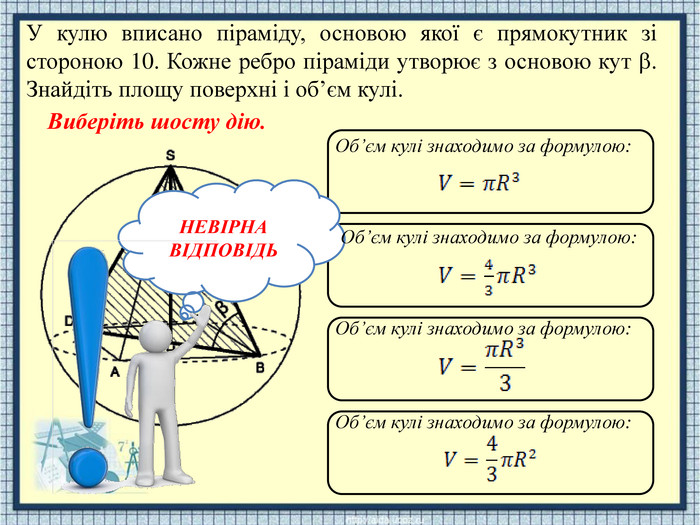
НЕВІРНАВІДПОВІДЬОб’єм кулі знаходимо за формулою: Об’єм кулі знаходимо за формулою: Об’єм кулі знаходимо за формулою: Об’єм кулі знаходимо за формулою: У кулю вписано піраміду, основою якої є прямокутник зі стороною 10. Кожне ребро піраміди утворює з основою кут . Знайдіть площу поверхні і об’єм кулі. Виберіть шосту дію.

1.2.3.4.5.6. У кулю вписано піраміду, основою якої є прямокутник зі стороною 10. Кожне ребро піраміди утворює з основою кут . Знайдіть площу поверхні і об’єм кулі. З того, що кути між ребрами і основою піраміди однакові ⟹ основа піраміди – квадрат. Знаходимо діагональ квадрату за формулою: З трикутника SHB знаходимо SB: З трикутника SDB знайдемо радіус кулі за теоремою синусів. Знаходимо площу поверхні кулі за формулою: Об’єм кулі знаходимо за формулою: Повне розв'язання задачі.

ЗАДАЧА №3 Знайдіть діагональ прямокутного паралелепіпеда, якщо вона нахилена до його грані під кутом 600, а сторони цієї грані дорівнюють 3 і 4.

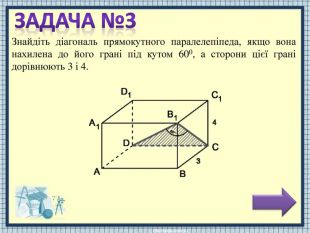
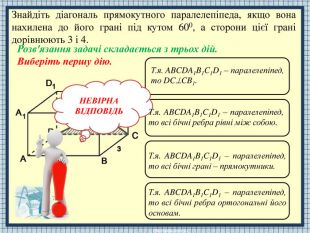
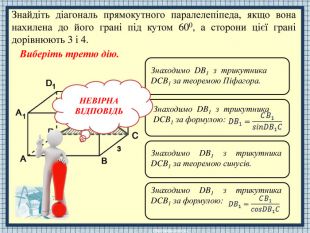
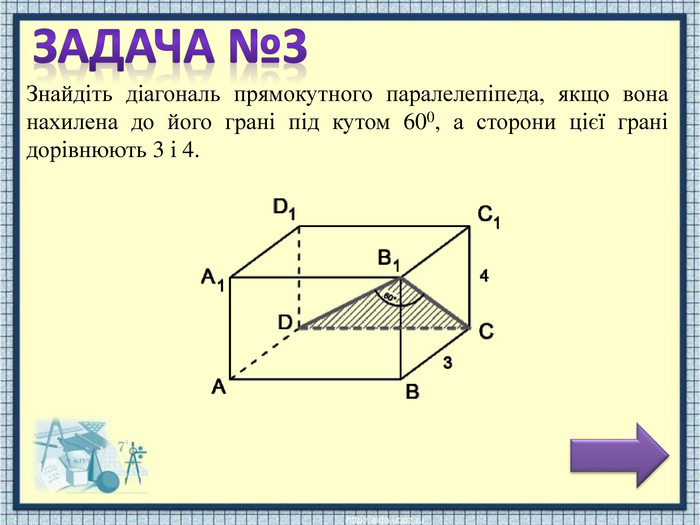
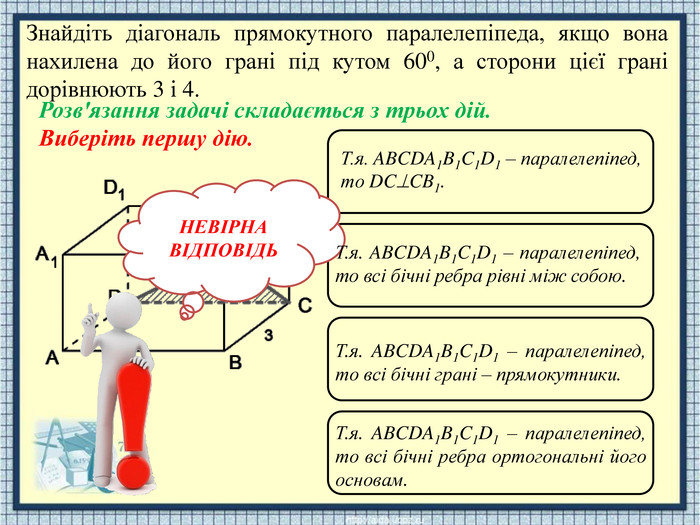
НЕВІРНАВІДПОВІДЬТ.я. ABCDA1 B1 C1 D1 – паралелепіпед, то DCCB1. Т.я. ABCDA1 B1 C1 D1 – паралелепіпед, то всі бічні ребра рівні між собою. Т.я. ABCDA1 B1 C1 D1 – паралелепіпед, то всі бічні грані – прямокутники. Т.я. ABCDA1 B1 C1 D1 – паралелепіпед, то всі бічні ребра ортогональні його основам. Знайдіть діагональ прямокутного паралелепіпеда, якщо вона нахилена до його грані під кутом 600, а сторони цієї грані дорівнюють 3 і 4. Розв'язання задачі складається з трьох дій. Виберіть першу дію.

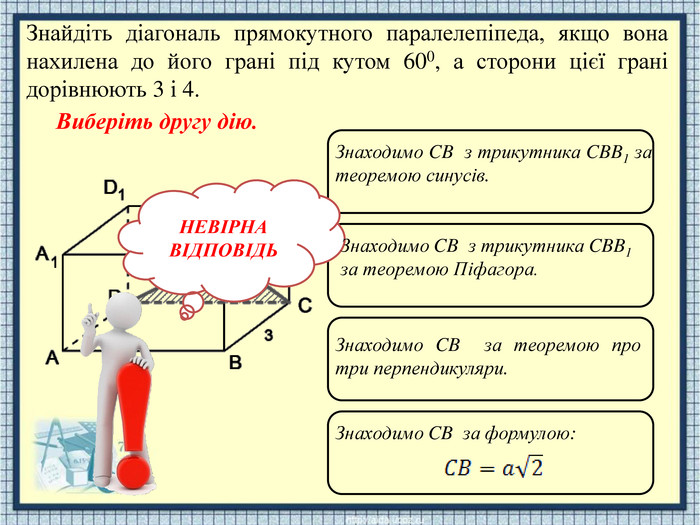
НЕВІРНАВІДПОВІДЬЗнаходимо CB з трикутника CBB1 за теоремою Піфагора. Знаходимо CB за теоремою про три перпендикуляри. Знаходимо CB з трикутника CBB1 за теоремою синусів. Знаходимо CB за формулою: Знайдіть діагональ прямокутного паралелепіпеда, якщо вона нахилена до його грані під кутом 600, а сторони цієї грані дорівнюють 3 і 4. Виберіть другу дію.

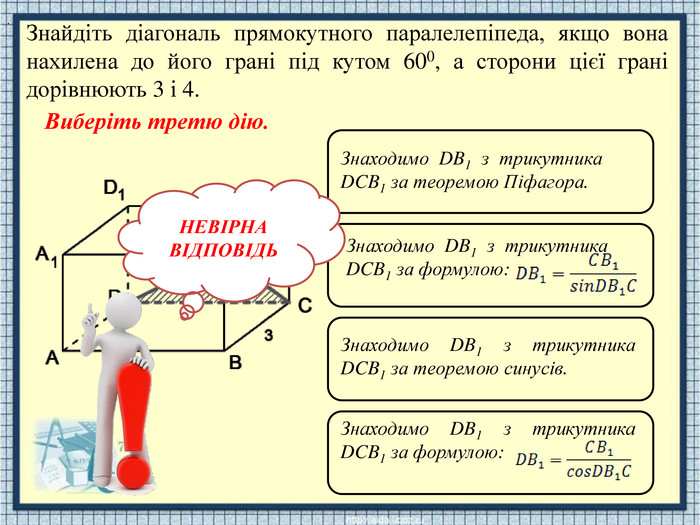
НЕВІРНАВІДПОВІДЬЗнаходимо DB1 з трикутника DCB1 за формулою: Знаходимо DB1 з трикутника DCB1 за теоремою синусів. Знаходимо DB1 з трикутника DCB1 за формулою: Знаходимо DB1 з трикутника DCB1 за теоремою Піфагора.. Знайдіть діагональ прямокутного паралелепіпеда, якщо вона нахилена до його грані під кутом 600, а сторони цієї грані дорівнюють 3 і 4. Виберіть третю дію.

Два кола з радіусами R=3 і r=1 дотикаються ззовні. Знайдіть відстань від точки дотику цих кіл до їх спільної дотичної.1.2.3. Т.я. ABCDA1 B1 C1 D1 – паралелепіпед, то DCCB1. Знаходимо CB з трикутника CBB1 за теоремою Піфагора. Знаходимо DB1 з трикутника DCB1 за формулою: Повне розв'язання задачі.