Класна робота

Урок на тему: «Одиничний вектор. Розклад вектора за трьома некомпланарними векторами»

Вектори називають компланарними, якщо вони лежать в одній або паралельних площинах.

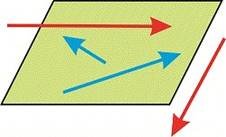
З цього слідує, що на площині (2D) всі вектори компланарні між собою. Що стосується тримірного простору (3D), то таке твердження не завжди вірне.

В тримірному просторі компланарними будуть кожні два вектори, оскільки через них можна провести паралельні площини.

Якщо маємо більше векторів, то для перевірки використовують необхідну і достатню умову компланарності трьох векторів у просторі.

Ознака компланарності трьох векторів

Якщо вектор можна подати у вигляді 𝑐⃗ = 𝑥𝑎⃗ + 𝑦𝑏⃗⃗, де х і у – деякі числа, то вектори

𝑎⃗, 𝑏⃗⃗, 𝑐⃗– компланарні.

Розкладання вектора за трьома некомпланарними векторами

Якщо вектори 𝑎⃗, 𝑏⃗⃗, 𝑐⃗ некомпланарні, то будь-який вектор 𝑑⃗можна подати у вигляді 

𝑑⃗ = 𝑥𝑎⃗ + 𝑦𝑏⃗⃗ + 𝑧𝑐⃗ , де х, у і z – деякі числа, причому такий розклад єдиний.

Координатні вектори (орти)

Одиничні вектори ⃗𝑒⃗⃗₁⃗ = (1; 0; 0), 𝑒⃗⃗⃗₂⃗ = (0; 1; 0), 𝑒⃗⃗⃗₃⃗ = (0; 0; 1),співнапрямлені з осями координат, називають координатними векторами, або ортами.

𝑚⃗⃗⃗ = 𝑎⃗𝑒⃗⃗₁⃗ + 𝑏𝑒⃗⃗⃗₂⃗ + 𝑐𝑒⃗⃗⃗₃⃗

Розкладання вектора за координатними векторами 

Будь-який вектор 𝑎⃗ = (𝑎₁; 𝑎₂; 𝑎₃)можна подати у вигляді 𝑎⃗ = 𝑎₁⃗𝑒⃗⃗₁⃗ + 𝑎₂𝑒⃗⃗⃗₂⃗ + 𝑎₃𝑒⃗⃗⃗₃⃗.

№ 1

Серед векторів 𝑎⃗ укажіть одиничні вектори.

Одиничними називають ті вектори, довжина (модуль) яких рівний 1.

|𝑎⃗| = √𝑎₁² + 𝑎₂² + 𝑎₃²

В даному завданні одиничними векторами є лише вектор 𝑐⃗ і 𝑑⃗, тому що:

            |𝑐⃗|  ;          |𝑑⃗| .

№ 2

Знайдіть координати одиничного вектора, який співнапрямлений з вектором:

1) 𝑎⃗(−3; 4; 0); 2) 𝑏⃗⃗(2; −3; −6); 3) 𝑐⃗(𝑘; 𝑚; 𝑝).

Розв’язання

1)  𝑎⃗(−3; 4; 0);             |𝑎⃗| ;        𝑒⃗⃗⃗₁⃗ = (−  ;  ; 0);

2)  𝑏⃗⃗(2; −3; −6);         |𝑏⃗⃗| ;      𝑒⃗⃗⃗₂⃗ = ( ; −  ; − );

3)  𝑐⃗(𝑘; 𝑚; 𝑝); |𝑐⃗| = √𝑘² + 𝑚² + 𝑝² ; 𝑒⃗⃗ ₂ ^𝑘_{2 2            2} ^𝑚_{2 2          2} ^𝑝_{2 2} .

√𝑘 +𝑚 +𝑝 √𝑘 +𝑚 +𝑝 √𝑘 +𝑚 +𝑝

№ 3

Дано одиничні вектори ⃗𝑒⃗⃗₁⃗ = (1; 0; 0), 𝑒⃗⃗⃗₂⃗ = (0; 1; 0), 𝑒⃗⃗⃗₃⃗ = (0; 0; 1). Знайдіть координати векторів: 1) 5⃗𝑒⃗⃗₁⃗ + 3𝑒⃗⃗⃗₂⃗ − 2𝑒⃗⃗⃗₃⃗; 2) 4⃗𝑒⃗⃗₁⃗ + 5⃗𝑒⃗⃗₃⃗;  3) 𝑚⃗𝑒⃗⃗₁⃗ − 𝑛𝑒⃗⃗⃗₂⃗ + 𝑘𝑒⃗⃗⃗₃⃗ .

Розв’язання

1)  𝑎⃗ = 5⃗𝑒⃗⃗₁⃗ + 3⃗𝑒⃗⃗₂⃗ − 2𝑒⃗⃗⃗₃⃗ = 5(1; 0; 0) + 3(0; 1; 0) − 2(0; 0; 1) = 𝑎⃗(5; 3; −2);

2)  𝑏⃗⃗ = 4⃗𝑒⃗⃗₁⃗ + 5⃗𝑒⃗⃗₃⃗ = 𝑏⃗⃗(4; 0; 5);

3)  𝑐⃗ = 𝑚⃗𝑒⃗⃗₁⃗ − 𝑛𝑒⃗⃗⃗₂⃗ + 𝑘𝑒⃗⃗⃗₃⃗ = 𝑐⃗(𝑚; −𝑛; 𝑘) .

№4

Розкладіть вектор 𝑚⃗⃗⃗(5; −17; 11)за векторами 𝑎⃗(3; −2; 0), 𝑏⃗⃗(−2; 4; 1)і 𝑐⃗(−1; −3; 4). Розв’язання

Будь-який вектор можна розкласти за векторами 𝑎⃗(3; −2; 0), 𝑏⃗⃗(−2; 4; 1)і 𝑐⃗(−1; −3; 4).

Отже, 𝑚⃗⃗⃗ = 𝜆𝑎⃗ + 𝜇𝑏⃗⃗ + 𝜐𝑐⃗ . Знайдемо 𝜆; 𝜇 і 𝜐 склавши систему рівнянь:

3𝜆 − 2𝜇 − 𝜐 = 5; {−2𝜆 + 4𝜇 − 3𝜐 = −17; 0𝜆 + 𝜇 + 4𝜐 = 11.

Розв’яжемо цю систему рівнянь.

𝜇 + 4𝜐 = 11; 𝜇 = 11 − 4𝜐.

                      3𝜆 − 2(11 − 4𝜐) − 𝜐 = 5;                    3𝜆 − 22 + 8𝜐 − 𝜐 = 5;

             {                                                           {

               −2𝜆 + 4(11 − 4𝜐) − 3𝜐 = −17;        −2𝜆 + 44 − 16𝜐 − 3𝜐 = −17;

            {       3𝜆 + 7𝜐 = 27;  ∙2    +{        6𝜆 + 14𝜐 = 54;   

                    −2𝜆 − 19𝜐 = −61;∙3          −6𝜆 − 57𝜐 = −183;