Урок 1. Лінійні рівняння з двома змінними

Для вивчення теми «Система лінійних рівнянь з двома змінними» спочатку необхідно розібратися, що таке  лінійне рівняння з двома змінними та його графік.

Для цього розглянемо задачу.

Для озеленіння та збагачення краси проспекту Гагаріна  в місті Харкові було посаджено 70 дерев сакури та магнолії. Скільки дерев кожного виду було посаджено у Харкові?

Пояснення. Позначимо кількість дерев сакури через х, а кількість дерев магнолії – у. Всього посадили (х + у) дерев, що за умовою задачі дорівнює 70.

Одержуємо рівняння: х + у= 70.

Маємо проблему: В РІВНЯННІ ДВА НЕВІДОМИХ.

Розв’язати таке рівняння звичайним способом ми не можемо, але можемо підібрати кілька пар таких чисел, які у сумі дають 70:

13 і 57; 42 і 28; 60 і 10 тощо.

Виникають питання:

-                       Що за рівняння ми одержимо?

-                       Як розв’язати це рівняння?

-                       Скільки розв’язків має рівняння?

def. Лінійним рівнянням з двома змінними називають рівняння виду ax+by=c, де x та y – змінні, a, b, c – числа (a, b – коефіцієнти при змінних, с – вільний член.) 

Наприклад, 2х – 3у = 6; −4х +  у = 1  

def. Розв’язком рівняння із двома змінними називають пару значень змінних, за яких рівняння перетворюються у правильну числову рівність.

Наприклад, пара чисел х = – 1 і у = 9 задовольняє рівнянню

 5х + 3у = 22, оскільки                                                                                                    .     

5(-1)+3×9=22.

 22=22 – істинна рівність, 

 Скорочено розв’язок записуючи (–1; 9), на І місці знаходиться х, а на ІІ – у. 

А пара чисел х = 1 і у = 2 це рівняння не задовольняє, оскільки  

 5*1 + 3*2 = 22

 11 ≠ 22 – не є істинною рівністю. 

 

 - Як розв’язати рівняння з двома змінними?

 

Щоб знайти розв’язок лінійного рівняння з двома змінними, можна підставити в рівняння довільне значення однієї змінної і розв’язавши одержане рівняння з однією змінною, знайти відповідне значення іншої змінної.

Наприклад. 3х – 5у = 1

Нехай х = 7, то 3*7 – 5у = 1

                        21 – 5у = 1                         –5у = –20                            у = 4 

Отже, (7; 4) – розв’язок.

Нехай х = –3, то 3*(–3) –5у = 1

                          –9 – 5у = 1                             –5у = 10                              у = –2

Отже, (–3; –2) – розв’язок.

Ми знайшли 2 розв’язки. Але (7; 4), (–3; –2) – не вичерпують всіх розв’язків Надаючи змінній х інших значень одержимо різні розв’язки рівняння, отже рівняння 3х – 5у = 1 має безліч розв’язків.

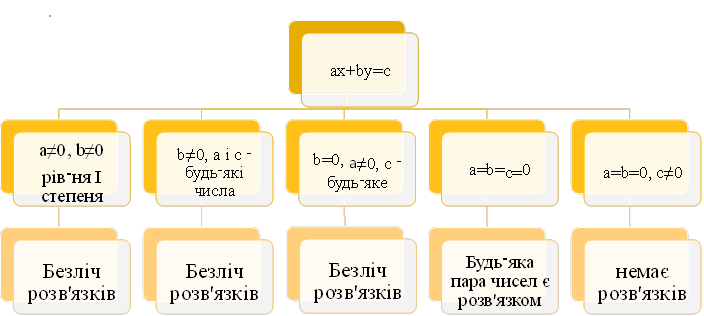
Залежно від того, яких значень набувають коефіцієнти a, b і c, лінійне рівняння з двома змінними ax + by = c може мати розв’язки або не мати їх.

 Рівняння ax + by = c не має розв’язків лише тоді, коли  a = 0, b = 0, а вільний член с ≠ 0. Тобто, 0x + 0y = c, а не існує такої пари значень х і у, яка б не задовольняла це рівняння.

В усіх інших випадках рівняння ax + by = c має безліч розв’язків.

Лише тоді, коли a ≠ 0, b ≠  0, значення х і у залежить один від одного,

𝑎            𝑐              𝑏              𝑐 тобто 𝑦 = −          𝑥 −            або  𝑥 = −  𝑦 −

                                  𝑏             𝑏                                 𝑎             𝑎

def. Рівняння ax + by = c, a ≠ 0, b ≠ 0, називається рівнянням І степеня з двома змінними, має безліч розв’язків.

Якщо хоча б один із коефіцієнтів дорівнює 0, тоді відповідно або у набуває лише одного числового значення, або х набуває будь-яких значень,  якщо a = 0, то 𝑦 = − ^𝑐, х – будь-яке число;

𝑏

якщо b = 0, то 𝑥 = − ^𝑐, у – будь – яке число.

𝑎

Якщо всі три коефіцієнта рівняння ax + by + с = 0 дорівнюють 0, то це рівняння задовольняє будь-яка пара чисел і таких пар – безліч.

 Взагалі, лінійне рівняння із двома змінними або має безліч розв’язків, або не має жодного.

def. Рівняння з двома змінними називають рівносильними, якщо вони мають одні і ті ж розв’язки або обидва рівняння не мають розв’язків.

Властивості рівнянь з двома змінними такі ж, як і властивості рівняння з однією змінною, а саме, якщо:

1)    в рівнянні розкрити дужки і звести подібні доданки;

2)    до обох частин рівняння додати (або відняти від них) той самий вираз;

3)    члени рівняння перенести з однієї частини в іншу, змінивши при цьому їх знаки на протилежні;

4)    обидві частини рівняння помножити (або розділити на одне й те ж саме відмінне від нуля число);

 то одержимо рівняння рівносильне даному.

 

 - Чи можна іншим способом розв’язати рівняння з двома змінними?

 

Розглянемо рівняння 5х + 4у = 16.

Використовуючи властивості рівнянь, виразимо одну змінну через іншу.

4у = 16 – 5х  | ÷4

_у = 16−5х

4 у =  4 –  х

Надаючи змінній х різних значень можна знайти відповідні значення у.

х = 4, то  у = 4  −  = 4 − 5 = −1; х = 8, то  у = 4 −  = 4 − 10 = −6; х= – 4, то  у = 4 − (−4) = 4 + ^5×4 = 9.

4×1

Отже, (4; –1); (8; –6); (–4; 9) – розв’язки рівняння.

Розв’яжемо разом Завдання 1.

Які з пар чисел (4; 1); (8; 2)  є розв’язком рівняння 3х + 4у = 16?

Розв’язання.

Оскільки (4;1) – розв’язок рівняння, то х = 4, у = 1, задовольняє рівняння

Підставимо:

     3 * 4 + 4 * 1 = 16

     12 + 4 = 16

     16 = 16 – істинна рівність, отже (4; 1) – розв’язок рівняння.

Оскільки (8; 2) – розв’язок рівняння, то х = 8, у = 2, задовольняє рівняння

Підставимо:

     3 * 8 + 4 * 2 = 16

     24 + 8 = 16

     32 ≠ 16 – не є істинною рівністю , отже (8; 2) – не є розв’язком.

Завдання 2.

Вирази змінну у через х та змінну х через у.

Рівняння	у через х	х через у
х – у = 2 х – 2у = 5	2 – х = у х − 5  = у 2	х= 2 + у х= 5 + 2у

 

 

Завдання 3.

 Визначить за якого значення b пара чисел (–4; 6) є одним із розв’язків лінійного рівняння х + by = 20.

Розв’язання.

Оскільки (–4; 6) – розв’язок рівняння, то значення –4 та 6 задовольняють рівнянню.

Підставимо,

–4 + 6b = 20 6b = 24 b = 4

Відповідь: Якщо b = 4, то (–4; 6) – розв’язок рівняння.

Завдання 4. Знайдіть таке число n, щоб пара чисел (n; – n) була розв’язком рівняння. Розв’язання.

5х + 4у = 3

 Оскільки (n;– n) – розв’язок рівняння, то підставивши в рівняння, одержимо

5n +4( – n)= 3 5n – 4 n = 3 n = 3 

Отже,  (3;-3) – розв’язок рівняння Задача 1. 

На танцювальний фестиваль приїхав ансамбль «Натхнення» із 18 школярів. Їх потрібно розмістити в кімнати або по 3, або 4 дитини. Скільки кімнат потрібно виділити для цього?

Розв’язання

Позначимо кількість  тримісних кімнат через х ,тоді чотиримісних – y.  

Всього потрібно (х + у) кімнат, що за умовою задачі дорівнює 18.

Одержимо рівняння х+ у=18.

Виразимо х через у: 

     3х = 18 – 4у,         x = ^18−4у

 3

 Перевіримо, за яких натуральних значень х набуває натурального

значення у.       якщо у = 1, то x = 4  – не задовольняє умові задачі якщо у = 2, то x = 3  – не задовольняє умові задачі.

якщо у = 3, то x = 2;  якщо у = 4, то x =  – не задовольняє умові задачі.

При x ˃ 4 змінна у набуває від’ємних значень. 

Отже, умову задовольняє одна пара натуральних чисел (2; 3).

 Отже,  

•      Рівняння виду ax + by = c, де x та y – змінні, a, b, c – числа називають лінійним рівнянням з двома змінними ( a ,b – коефіцієнти при змінних, с – вільний член) 

•      Розв’язком рівняння із двома змінними називають пару значень змінних, за яких рівняння перетворюються у правильну числову рівність.

•      Лінійне рівняння із двома змінними або має безліч розв’язків, або не має жодного розв’язку.

 

Алгоритм розв’язування лінійного рівняння з двома змінними:

1.                 підставити в рівняння довільне значення однієї змінної;

2.                 розв’язавши одержане рівняння з однією змінною, знайти відповідне    значення іншої змінної; або

1.   виразити одну змінну через іншу;

2.   надаючи змінній х різних значень, знайти відповідні значення у.

                Одержимо пару чисел яка є розв’язком рівняння.