Науково-пошукова робота

Тригонометрія навколо нас

 

 

 

 

 

 

 

Петрів Н.В.

Зміст

 

 Вступ

1. Історія науки

2. Складові науки

3. Розвиток та елементи

4. Застосування на практиці

 Висновок

Джерела інформації

 

 

 

 

 

 

 

 

 

 

 

 

 

Вступ

 

     Ми зараз живемо у епоху, коли ми дуже швидко розвиваємося, маємо великі можливості, необмежений доступ до інформації, і доступ до різних приладів. Але мало хто замислюється, а ще менше дізнаються, дякуючи чому це все. І велику роль в цьому відіграє тригонометрія.

     Об’єкт дослідження: тригонометрія, практичне її застосування, значення її  в науці.

      Мета дослідження: показати, доказати важливість, вплив тригонометрії на розвиток тих чи інших наук, а також на наше життя.

      Методи дослідження: пошук інформації.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1. Історія науки

 

     Перш за все варто почати з історії цієї науки.

     Історія тригонометрії як науки про співвідношення між кутами і сторонами трикутника та інших геометричних фігур охоплює понад два тисячоліття. Більшість таких співвідношень неможливо виразити за допомогою звичайних алгебраїчних операцій, тому знадобилось ввести особливі тригонометричні функції, які спершу оформлювали у вигляді таблиць.

     Історики вважають, що тригонометрію створили стародавні астрономи, трохи пізніше її почали використовувати в геодезії й архітектурі. З часом сфера застосування тригонометрії постійно розширювалась, в теперішній час її використовують майже всі природничі науки, техніка і низка інших галузей діяльності. Тригонометричні функції виявились особливо корисними для вивчення коливних процесів; на них заснований також гармонічний аналіз функцій та інші інструменти аналізу. Томас Пейн у своїй книзі «Доба Розуму» (1794) назвав тригонометрію «душею науки».

     Зародки тригонометрії можна знайти в математичних рукописах стародавнього Єгипту, Вавилона і стародавнього Китаю.

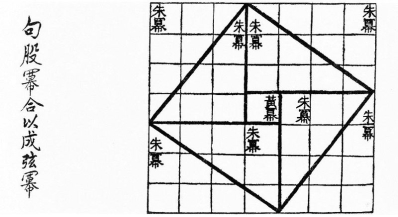
     Від вавилонської математики бере початок звичайне для нас вимірювання кутів градусами, мінутами і секундами (введення цих одиниць у давньогрецьку математику зазвичай приписують Гіпсиклу, II століття до н. е.) Серед теорем, відомих вавилонцям, була, приміром, така: вписаний кут, що спирається на діаметр кола — прямий. Головним досягненням цього періоду стало співвідношення, яке згодом отримало назву теореми Піфагора; Ван дер Варден вважає, що вавилонці відкрили його між 2000 і 1786 роками до н. е. Цілком можливо, що китайці відкрили його незалежно (див. «Математика в дев'яти книгах»). Незрозуміло, чи знали загальне формулювання теореми стародавні єгиптяни, однак прямокутний «єгипетський трикутник» зі сторонами 3, 4, і 5 був там добре відомий і широко використовувався..

Давньогрецька ілюстрація до теореми Піфагора

Загальне і логічно зв’язне викладення тригонометричних співвідношень з'явилося в давньогрецькій геометрії. Грецькі математики ще не виділяли тригонометрію як окрему науку, для них вона була частиною астрономії.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2. Складові тригонометрії

Плоска тригонометрія

    Декілька теорем тригонометричного характеру містять «Начала» Евкліда (IV століття до н. е.). В першій книзі «Начал» теореми 18 і 19 встановлюють, що більшій стороні трикутника відповідає більший протилежний кут — і навпаки, більшому куту відповідає більша сторона. Теореми 20 і 22 формулюють «нерівність трикутника»: з трьох відрізків можна скласти трикутник тоді і тільки тоді, коли довжина кожного менше суми довжин двох інших. Теорема 32 доводить, що сума кутів трикутника дорівнює 180°.

     Наступна теорема 13 є варіантом теореми косинусів для гострокутних трикутників. Аналогу теореми синусів у греків не було, це найважливіше відкриття було зроблене значно пізніше.

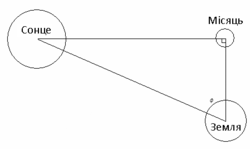
      Прямокутний трикутник Аристарха: взаємне розташування Сонця, Місяця і Землі під час квадратури

      Подальший розвиток тригонометрії пов'язаний з ім'ям астронома Аристарха Самоського (III століття до н. е.). В його трактаті «Про величини і відстані Сонця і Місяця» була поставлена задача про визначення відстаней до небесних тіл; ця задача потребувала обчислення співвідношення сторін прямокутного трикутника при відомому значенні одного з кутів. Аристарх розглядав прямокутний трикутник, утворений Сонцем, Місяцем і Землею під час квадратури. Йому було потрібно обчислити величину гіпотенузи (відстань від Землі до Сонця) через катет (відстань від Землі до Місяця) при відомому значенні прилеглого кута (87°), що є еквівалентом обчислення значення. За оцінкою Аристарха, ця величина лежить у проміжку від 1/20 до 1/18, тобто відстань до сонця у 20 разів більше, ніж до Місяця; насправді Сонце знаходиться майже у 400 разі далі, ніж Місяць, помилка виникла через неточність у вимірюванні кута. Водночас Аристарх довів нерівність, яка у сучасних термінах передається формулою:

<<

      Ця ж нерівність міститься в «Обчисленні піщинок» Архімеда. В працях Архімеда (III століття до н. е.) наводиться важлива теорема ділення хорд, яка по суті еквівалентна формулі синуса половинного кута:

=

      Греки також вирішили проблему побудови трикутника за його трьома заданими елементами (з яких хоча б один є стороною) Протягом всього періоду розвитку античної науки головною нивою для застосування результатів плоскої тригонометрії у греків залишалась астрономія. Окрім задачі з обчислення відстаней, тригонометрію залучали для визначення параметрі руху світила у просторі.

      Замість сучасної функції синуса Гіппарх та інші давньогрецькі математики звичайно розглядали залежність довжини хорди кола від заданого центрального кута (чи, що еквівалентно, від заданої дуги кола, вираженої у кутовій мірі). У сучасній термінології, довжина хорди, що стягує дугу θ одиничного кола дорівнює подвоєному синусу центрального кута θ/2. Ця відповідність справедлива для будь-яких кутів: 0 < θ < 360°. Мовою хорд були сформульовані перші відкриті греками тригонометричні співвідношення.

       Основним досягненням античної тригонометричної теорії став розв'язок у загальному вигляді задачі «розв'язування трикутників», тобто заходження невідомих елементів трикутника, коли відомі його три елементи (з яких хоча б одним є стороною). Пізніше ця задача і її узагальнення стали основною задачею тригонометрії: задані декілька (звичайно три) відомих елементи трикутника, вимагається знайти решту пов'язаних з ними величин. Спершу до числа елементів трикутника (відомих і невідомих) включали сторони і кути при їх вершинах, пізніше до них додались медіани, висоти, бісектриси, радіус вписаного і описаного кола, розташування центру ваги тощо. Прикладні тригонометричні задачі відрізняються великою різноманітністю — наприклад, можуть бути задані невидимі на практиці результаті дій над перерахованими величинами (приміром, сума кутів чи відношення довжин сторін.

 

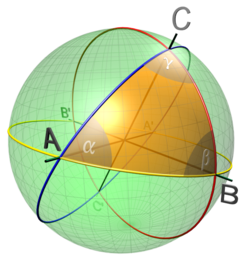
Сферична тригонометрія

      Паралельно з розвитком тригонометрії площини греки, під впливом астрономії, значно розвинули сферичну тригонометрію. В «Началах» Евкліда з цієї теми є тільки одна теорема про співвідношення об'ємів шарів різного діаметра, але потреби астрономії і картографії зумовили швидкий розвиток сферичної тригонометрії і суміжних з нею областей — системи небесних координат, теорії картографічних проекцій, технології астрономічних приладів (зокрема, була винайдена астролябія).

       Історики дійшли згоди щодо ступеню розвитку у античних греків геометрії небесної сфери. Деякі дослідники наводять аргументи, що екліптичну чи екваторіальну систему координат використовували для запису результатів астрономічних спостережень принаймні вже у час Гіппарха. Можливо тоді були відомі і деякі теореми сферичної тригонометрії, які могли використовуватись для складення зоряних каталогів і в геодезії.

      Перші відомі в наш час праці зі «Сферики» (тобто сферичної геометрії, з очевидним астрономічним нахилом) написали:

(IV століття до н. е.) Автолік з Пітани і Евклід («Феномени»).

(II століття до н. е.) Феодосій і Гіпсикл.

      Деякі задачі розглянуті в цих творах мають тригонометричний характер, проте через слабку розробленість теорії автори ще користуються обхідними шляхами. Наприклад, задачу «знайти час повного сходу (заходу) зодіакального сузір'я» Гіпсикл вирішує наближено за допомогою многокутних чисел.

Сферичний трикутник

      Вирішальним етапом в розвитку теорії стала монографія «Сферика» в трьох книгах, яку написав Менелай Александрійський (близько 100 року н. е.).

      Кілька десятиліть потому Клавдій Птолемей у своїх працях «Географія», «Аналемма» і «Планісферій» приводить докладне викладення застосування тригонометрії до картографії, астрономії і механіки. Серед іншого, описана стереографічна проекція, досліджені кілька практичних задач, наприклад: визначити висоту і азимут небесного світила за його схиленням і часовим кутом. З точки зору тригонометрії, це означає, що потрібно знайти сторону сферичного трикутника за двома іншими сторонами і протилежним кутом.

        Сферичній геометрії Птолемей також присвятив XIII главу в першій книзі «Амельгеста»; на відміну від Менелая, Птолемей не привів доведень багатьох тверджень, але натомість приділив багато уваги алгоритмам, придатним для практичних обчислень в астрономії. Опорною конструкцією в «Амальгесті» слугує, замість плоских хорд, «чотиристоронник Менелая». Для вирішення прямокутного сферичного трикутника, тобто для обчислення його характеристик, Птолемей навів у словесній формі 4 теореми.

 

 

 

3. Розвиток та елементи

XVI–XVII століття

       Розвиток тригонометрії у Новий час став надзвичайно важливим не тільки для астрономії та астрології, але й для інших галузей, в першу чергу артилерії, оптики і навігації у далеких морських подорожах. Тому після XVI століття цією темою займалися багато видатних вчених, в тому числі Миколай Коперник, Йоганн Кеплер, Франсуа Вієт.

      Потреба у складних тригонометричних розрахунках викликала на початку XVII століття відкриття логарифмів, причому перші логарифмічні таблиці Джона Непера містили тільки логарифми тригонометричних функцій. Серед інших відкриттів Непера — ефективний аглоритм розв'язання сферичних трикутників, що отримав назву «формули аналогії Непера».

      Термін «тригонометрія» як назву математичної дисципліни вів в обіг німецький математик Б. Пітискус, який облікував у 1595 році книгу «Тригонометрія, або стислий і ясний трактат про розв'язування трикутників» (лат. Trigonometria: sive de solutione triangulorum tractatus brevis et perspicuous). До кінця XVII століття з'явились сучасні назви тригонометричних функцій. Термін синус вперше застосував близько 1145 року англійський математик і арабіст Роберт Честерський. Регімонтан у своїй книзі назвав косинус «синусом доповнення» (лат. sinus complementi), оскільки його послідовники у XVII столітті скоротили це позначення до co-sinus (Едмунд Гунтер), а пізніше — до cos (Вільям Отред). Назви тангенса і секанса запропонував у 1583 році данський математик Томас Фінке (ThomasFincke). в згаданий вище Едмунд Гунтер ввів назви котангенса і косеканса. Термін «тригонометричні функції» вперше застосував у своїй «Аналітичній тригонометрії» (1770) Георг Симон Клюгель.

Реформи Леонарда Ейлера

Леонард Ейлер

      Сучасного вигляду тригонометрії надав Леонард Ейлер. В трактаті «Введення в аналіз нескінченних» (1748) Ейлер навів визначення тригонометричних функцій, еквівалентне сучасному, і відповідно визначив обернені функції. Якщо його попередники розуміли синус та інші поняття геометрично, тобто як лінії в колі чи трикутнику, то після робіт Ейлера стали розглядатися як безрозмірні аналітичні функції дійсного і комплексного змінного. Для комплексного випадку він встановив зв'язок тригонометричних функцій з показниковою функцією (формула Ейлера). Підхід Ейлера з тих пір став загальновизнаним і увійшов до підручників.

        Ейлер розглядав як допустимі від'ємні кути і кути більше 360°, що дозволило визначити тригонометричні функції на всій дійсній числовій прямій, а потім продовжити їх на комплексну площину. Коли постало питання про поширення тригонометричних функцій на тупі кути, знаки цих функцій до Ейлера часто обирались помилково; багато математиків вважали, наприклад, косинус і тангенс тупого кута додатними. Ейлер визначив ці знаки для кутів у різних координатних квадрантах, виходячи з формул зведення.

XIX–XXI століття

       На початку XIX століття М. І. Лобачевський додав до плоскої і сферичної тригонометрії третій розділ — гіперболічну (для геометрії Лобачевського, першу роботу в цій галузі опублікував Ф. А. Таурінус у 1826 році). Лобачевський показав, що формули сферичної тригонометрії переходять у формули гіперболічної тригонометрії при заміні довжин сторін трикутника a, b, c на уявні величини: ai, bi, ci — чи, що еквівалентно, при заміні тригонометричних функцій на відповідні гіперболічні.

       У XIX–XX століттях стрімкого розвитку набули теорія тригонометричних рядів і пов'язані з нею області математики: гармонічний аналіз, теорія випадкових процесів, кодування аудіо і відеоінформаціїта інші. Ще Даниїл Бернуллі висловив думку, що будь-яку (неперервну) функцію на заданому проміжку можна представити тригонометричним рядом.

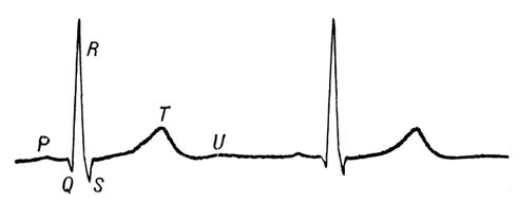
Тригонометричні функції

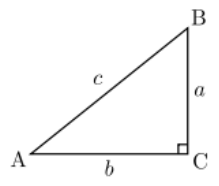
Тригонометрія ґрунтується на співвідношенні подібності. Трикутники з двома рівними кутами подібні, тому подібні прямокутні трикутники, в яких рівний один гострий кут. Відношення довжин сторін у подібних трикутників однакове, тому відношення сторін прямокутних трикутників залежить тільки від одного параметра — величини гострого кута. Ця обставина дозволяє означити тригонометричні функції: синус, косинус, тангенс, котангенс, секанс і косеканс, через відношення різних сторін прямокутного трикутника.

Нехай ABC — прямокутний трикутник. C — вершина прямого кута, AB — гіпотенуза, AC і BC — катети, α — кут BAC

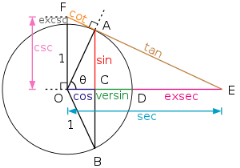
Тригонометричні функції кута θ всередині одиничного кола

      У XVIII столітті Леонард Ейлер дав сучасні, загальніші визначення, розширивши область визначення цих функцій на всю числову вісь. Якщо розглянути у прямокутній системі координат коло одиничного радіуса (див. малюнок) і відкласти від горизонтальної осі кут (додатня величина кута відкладається проти годинникової стрілки, у протилежному випадку — за годинниковою стрілкою). Точку перетину побудованої сторони кута з колом позначено A. Тоді:

• Синус кута визначається як ордината точки A.
• Косинус — абсциса точки A.
• Тангенс — відношення синуса до косинуса.
• Котангенс — відношення косинуса до синуса (тобто величина, обернена до тангенса).
• Секанс — величина, обернена до косинуса.
• Косеканс — величина, обернена до синуса.

Для гострих кутів нові визначення збігаються з попередніми.

      Можливим є також чисто аналітичне визначення цих функцій, що не пов'язане з геометрією і представляє кожну функцію її розкладанням у нескінчений ряд.

 

 

 

 

 

 

 

 

 

 

4. Застосування

 

     Тригонометричні обчислення застосовуються практично у всіх областях геометрії, фізики й інженерної справи. Велике значення має техніка тріангуляції, що дозволяє вимірювати відстані до недалеких зірок в астрономії, між орієнтирами в географії, контролювати системи навігації супутників. Також слід відзначити застосування тригонометрії в таких областях, як теорія музики, акустика, оптика, аналіз фінансових ринків, електроніка, теорія ймовірностей, статистика, біологія, медицина (включаючи ультразвукове дослідження (УЗД) і комп'ютерну томографію), фармацевтика, хімія, теорія чисел (і криптографія), сейсмологія, метеорологія, океанологія, картографія, фізика, топографія та геодезія, архітектура, фонетика, економіка, електронна техніка, машинобудування, комп'ютерна графіка, кристалографія.

 

Фізика і тригонометрія

Гармонічні коливання

За допомогою тригонометричних функцій можна описати гармонічні коливання

 

 

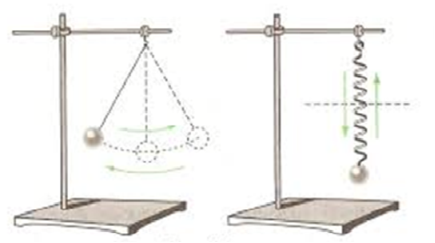
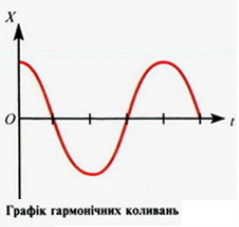
     Гармонічними коливаннями називаються періодичні коливання фізичної величини (або будь-якої іншої) залежно від часу, які відбуваються згідно із законами синуса або косинуса.

     Тягарець, що коливається на нитці, — це приклад найпростішого маятника.

     Маятник — це тверде тіло, яке здійснює коливання під впливом притягання до Землі або під впливом дії пружини.

     Отже за допомогою найпростішого маятника, коливання якого і принцип дії основуються на законах синусу и косинусу, ми зараз можемо використовувати такі речі як годинники, сейсмографи, навігаційні прилади.

     Продовжуючи тему тригонометрія у фізиці, варто зазначити ще таке явище як-синусоїдний струм.

Синусоїдний струм та основні величини, що його характеризують

Синусоїдний струм - струм, що змінюється у часі за синусоїдним законом:, де максимальне значення функції - амплітуда. 

Амплітуду струму позначають І_m 

.  - фаза синусоїдної функції – числове значення її величини в даний момент часу.

• - початкова фаза – значення фази в момент часу 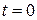 , вона може бути додатня або від’ємна, і визначаєтьс явід точки, де функція міняє знак «-» на «+», до початку координат. На Рис. 1 початкова фаза додатня.
• Період Т - це час, за який здійснюється одне повне коливання.
•  Частота f - число коливань за 1 секунду,  , вимірюється в 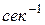 або в Герцах (Гц).

     Більшість електровимірювальних приладів (наприклад, електромагнітної системи) показують не амплітуду і не середнє значення, а, так зване, діюче або ефективне значення синусоїдної величини. Діюче значення синусоїдного струму період якого Т, дорівнює значенню такого еквівалентного постійного струму, який проходячи по тому ж опору, що й синусоїдний, за час Т виділяє на ньому ту ж кількість енергії.

Закінчуючи тему фізики, варто зазначити  про таку річ як джерело безперебійного живлення(ДБЖ)

     Джерело Безперебійного живлення-автоматичний пристрій, що дозволяє підключеному обладнанню деякий (як правило — нетривалий) час працювати від акумуляторів ДБЖ, при зникненні електричного струму або при відхиленні його параметрів від допустимих норм. Крім того, воно здатне змінювати параметри (напругу, частоту) електроживлення для досягнення рекомендованих. Часто застосовується для забезпечення безперебійної роботи комп'ютерів. Може поєднуватися з різними видами генераторів електроенергії.

З нашого життя ми можемо знати такі приклади ДБЖ як: спеціально зроблені для комп’ютерів, для будинків, генератори, звичайні павербанки для зарядки як правило телефону.

 Роль синусоїди у цьому. Коли споживачі купляють ДБЖ вони звісно цікавляться характеристиками, але майже ніколи не звертають увагу  на такі параметри як-  алгоритм роботи і потужність зарядного пристрою або сумісність ДБЖ з бензо електростанціями. Але це і є найголовніше. Існує параметр, що часто скорочує список кандидатів на пост домашнього безперебійника у декілька разів. Параметр цей-форма вихідної напруги інвертора ДБЖ.

 

За формою вихідноїнапруги ДБЖ, найчастіше, діляться на два типи:

- модифікована синусоїда («квазісинусоїда»)

- синусоїда («правильна» синусоїда, «чиста» синусоїда)

     Різниця між 2 типами полягає у тому, що модифікована синусоїда–не що інше, як ступінчаста різнополярна крива напруги і графік y=sinx вона нагадує дуже віддалено.  Для досягнення такого режиму роботи інвертора не потрібна складна схемотехніка і дорогі комплектуючі. Такі ДБЖ переважно використовуються у комп’ютерах,  павербанках. Це все через те, що модифікована синусоїда не розрахована для великих напруг.

     «Чиста синусоїда»– форма напруги, що не відрізняється від присутньої в міській електромережі. Хоча, і тут можна зробити поправку. Буває, що синусоїда високоякісного ДБЖ більше схожа на математичний графік (близька до ідеалу), чим синусоїда в мережі змінного струму. Уся справа в недосконалості ліній електропередач  і великій кількості споживачів реактивного характеру. Як наслідок – спотворення. Коли споживачі використовують ДБЖ із “чистою синусоїдою” у них практично немає обмежень, крім одного-максмимальної потужності.

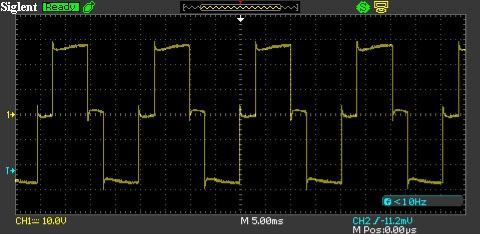
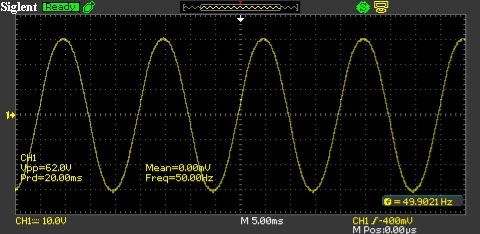
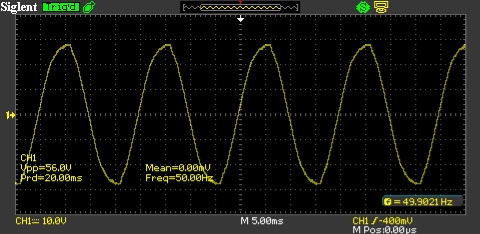
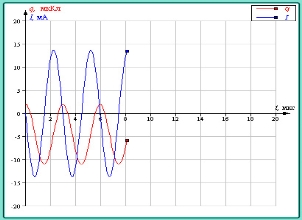
Рисунок1 Осцилограма вихідної напруги ДБЖ «квазісинусного» типу

Рисунок2 Осцилограма напруги міської мережі змінного струму.

Рисунок3 Осцилограма вихідної напруги ДБЖ UPS-0512.

Сейсмологія і тригонометрія

     Використовуючи свідчення сейсмографів (приладів, які безперервно фіксують коливання ґрунту і будують спеціальні графіки – сейсмограми), геологи можуть передбачити наближення землетрусу або цунамі.

Радіохвилі та звукові хвилі і тригонометрія

     Радіохвилі — діапазон електромагнітних ХВИЛЬ.

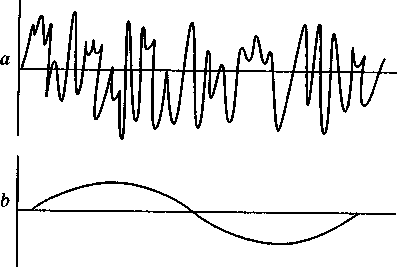
     Усі коливання хвиль пояснюються тригонометричними поняттями,а самі коливання у багатьох випадках є повторення синусоїди.

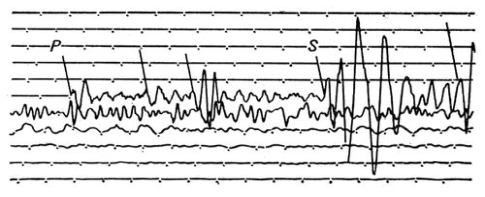
Медицина і тригонометрія

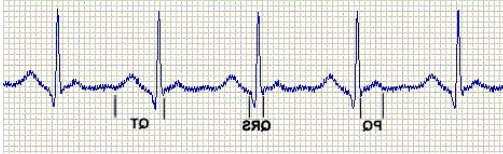
     В медицині для перевірки серця використовуються кардіограми, які періодично повторюються, що вказує на їх коливання та схожість з синусоїдою.

Спорт і тригонометрія

      У таких видах спору як фігурне катання, хокей, гребля, лижі присутні коливальні рухи при зміні положення тіла спортсмена

      Тригонометрія присутня ще у багатьох проявах.

      Наприклад, коливальний рух голови папуги,винирювання кита з води, змахи крил птахів, схожість архітектурних витворів синусоїдою тощо.

 

 

 

 

 

 

 

 

 

 

Висновок

 

      У висновку хочемо зазначити,що тригонометрія широко розповсюдженна наука,яка тісно повязана з фізикою, медициною,географією, із спортом, і оточуючим середовищем. Дякуючи їй ми зараз маємо багато речей без яких не можем уявити наше життя, деяким вона рятує життя, і навіть якщо вона не використовується напряму для якихось обчислень, то обриси певних складових тригонометрії можна помітити у дуже багатьох речах.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Список використаних джерел

 

1. http://phantom-energy.com.ua/uk/article/pochemu-sinusoida-/
2. https://uk.wikipedia.org/wiki/Гармонічні_коливання
3. http://studopedia.com.ua/1_310922_sinusoidniy-strum-ta-osnovni-velichini-shcho-yogo-harakterizuyut.html
4. https://disted.edu.vn.ua/courses/learn/8706

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

РЕЦЕНЗІЯ

 

на науково-пошукову роботу учня навчально-виховного комплексу  "Інженерно-економічної школи – Львівського економічного ліцею" Кіщака Ореста і Скаска Василя, учнів 11 групи.

 

Тема “ Тригонометрія навколо нас”.

      Пошукова робота включає вступ, 4 розділи, висновок, список використаної літератури. Ця робота викладена на актуальну тему так, як освітлює питання “ Застосування тригонометрії на практиці ”, за редакцією якого зроблені висновки.

       Зміст даної роботи викладений на достатньому теоретичному рівні, має практичні значення, достатньо глибоко в логічній послідовності викладенні теоретичні питання і практичні застосування. Дипломна робота в цілому відповідає вимогам кваліфікаційного рівня та заслуговує позитивної оцінки.

 

 

Рецензент:

вчитель математики

 Петрів Н.В.