Конспект інтегрованого уроку алгебри та геометрії в 8 класі з теми " Тотожні перетворення виразів, які містять квадратні корені. Теорема Піфагора."

               ВІДДІЛ  ОСВІТИ  ДОБРОПІЛЬСЬКОЇ  МІСЬКОЇ  РАДИ

 

Добропільський навчально – виховний комплекс

                          «Загальноосвітня школа    І-ІІІ ступенів  №3 – дошкільний

навчальний заклад»

 

 

 

 

Конспект

інтегрованого уроку

в 8 класі

«Тотожні перетворення виразів,

які містять квадратні корені.

Теорема Піфагора.»

                                                   Підготувала вчитель  математики

                                                                 Чухліб Олена Дмитрівна

.

 

 

 

 

 

 

 

 

 

 

м. Добропілля

2019 р.

Тема. Тотожні перетворення виразів, які містять квадратні корені. Теорема Піфагора.

8 клас

Тип уроку.  Урок застосування знань і вмінь.

Мета. Формування компетентностей:

 Предметна: узагальнити знання та вміння застосувати властивості арифметичного квадратного кореня для перетворення виразів;

закріпити теорему Піфагора при  розв'язуванні задач.

  Соціальна та громадянська: розвивати увагу, пам’ять, логічне мислення, активізувати пізнавальну активність учнів; формувати вміння аналізувати інформацію;

виховувати  інтерес до вивчення математики; культуру спілкування, поведінки  та математичної грамотності.

Ключові: уміння вчитися впродовж життя – відбирати і застосовувати потрібні знання та способи діяльності для досягнення мети.

Форма проведення уроку: інтегрований урок алгебри та геометрії.

Обладнання: роздатковий матеріал ( квадрати та прямокутники різних розмірів на кожній парті),   презентація до уроку;  тест  в програмі « My test Student(Pro)», завдання на картках для роботи в групах та індивідуальної роботи.

Методи форми та прийоми навчання: мозковий штурм, індивідуальна робота,   практична робота в групі,  самостійна робота.

                                        Хід уроку.

1. Організаційний момент.  Привітання.
2.   Повідомлення теми і мети уроку. Мотивація навчання.

           Ключове слово сьогоднішнього уроку ви відгадаєте, якщо дасте відповідь на такі запитання:

1) підземна частина рослини;
2) розв’язок  рівняння;
3) спільна частина споріднених слів.

 

  Або розгадаєте ребус.

 

 

(Корінь).

 Отже ключовим словом буде корінь.

А про який корінь можна говорити на алгебрі?

Арифметичний квадратний корінь, корінь рівняння.

Епіграф  «Знати – це означає насамперед уміти користуватись знаннями»

   3. Перевірка домашнього завдання.

1. Помічники перевіряють  наявність  домашнього завдання на перерві і звітують про результати перевірки.

У класі: правильне розв’язання наведене на слайдах презентації, разом перевіряємо відповіді.

4. Актуалізація опорних знань  (Вправа «Мікрофон»)

А які знання ми маємо? Що нам сьогодні згодиться на уроці? Давайте пригадаємо.

1.  Арифметичним квадратним коренем із числа а називається…невід’ємне число, квадрат якого дорівнює а.
2.  Вираз 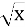      не має змісту при …   x<0
3. При яких значеннях а має корені рівняння х² = а? ?

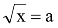                                                                                                 При а≥0

4. Скільки коренів має рівняння х² = а?  

                   Два, якщо а>0; один, якщо а=0; жодного, якщо а˂0.

5. Скільки коренів має рівняння ?

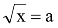                                                Один корінь а²_, при а ≥0_; жодного, при а<0.

6.             Щоб внести додатний множник під знак кореня треба … піднести  його до квадрату і помножити на підкореневий вираз.

7.             Щоб винести множник з-під знака кореня треба…розкласти підкореневий вираз на множники так, щоб з одного множника корінь добувався і добути його.

Теорію ви засвоїли, а тепер спробуйте використати ці знання для перевірки правильності розв’язування вправ.

5. Застосування знань і вмінь. Розв´язування вправ.

Біля дошки працюють самостійно 2 учня (завдання на картках) і 2 учні проходять тести на комп´ютерах.

Картка1.

1. Обчислити: –

2. Спростити вираз: + - 6.

3. Скоротити дріб:.

 

Картка2.

1. Обчислити:  - ·.

2. Спростити вираз: - )·.

3. Скоротити дріб:.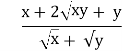

 

Разом з учнями розв’язуємо приклади зі слайдів:

1. Знайдіть арифметичний квадратний корінь з даних чисел: ; .

 

2. Виконайте дії:

-6а +8а;

(а-2)(а+2);

( -2) ( +2)

     √9х +√36х - √25х.

3. Винесіть множник з-під знака кореня:

;

4. Внесіть множник під знака кореня:

;

5. Розкладіть на множники:

С² -10;

+ ;

- .

6. Скоротити дроби:    ;      .

6. Фізкультхвилинка.

Давайте відпочинемо: разом проспіваємо пісню про математику, при цьому робимо відповідні  ритмічні рухи.

1. Эй, народ честной, посмотри вокруг:
   Чертим на доске мы ромб, квадрат и круг.
   У нас нету проблем. 
   Мы скажем всем,
   Кто здесь повелитель уравнений и схем
   
    
2. ПРИПЕВ :
   Извлекаем корень,
   Сокращаем дроби
   
   2) Эй, учителя, слушайте сюда,
   Каждому известно что на свете 
   Всего одна царица наук. 
   А ну-ка без рук, с нами согласится даже физрук
   
   ПРИПЕВ:
   Извлекаем корень,
   Сокращаем дроби
   
   3) Ну-ка, малышня, посмотри сюда!
   Если не учить математику,
   То ждет беда.
   А ну-ка взбодрись и встрепенись. 
   Математика - это вся наша жизнь!
   ПРИПЕВ:
   Извлекаем корень,
   Сокращаем дроби – 3 раза

 

7.  Ця тема дуже тісно пов’язана з такими задачами:

Задача1. Знайти гіпотенузу прямокутного трикутника за відомими катетами а=2см, b=3см:
А чому дорівнює  гіпотенуза с?

Задача 2 . Обчисліть довжину драбини, яку потрібно поставити до стіни висотою 3 м на відстані 2 м від стіни.

Чи могли б ми розв’язати ці задачі, якби не знали як добувати корені?

Тому зараз розшифруйте слова, записані в таблицях, попередньо знайшовши значення даних виразів:

Відповідь: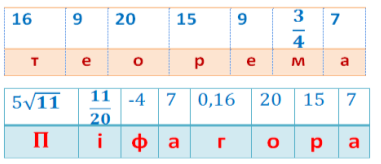
 

8. Практична робота (робота в групах)

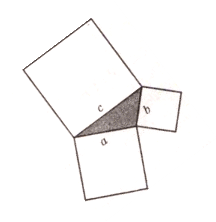
Так, теорема Піфагора. Отже, давайте її сформулюємо та доведемо.

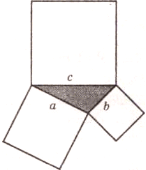
І. Учні працюють з роздатковим матеріалом, який допомагає наочно побачити доведення теореми Піфагора.( За допомогою площ квадратів).

Оскільки квадрати відрізків а, Ь, с до­рівнюють площам квадратів з такими самими сторонами, то теорему Піфагора часто форму­люють і так: площа квадрата, побудованого на гіпотенузі прямокутного трикутника, дорівнює сумі  площ квадратів, побудованих на його ка­тетах.(1)

.

 

 

                                     b

             a            

 

     Учні працюють в 4-х групах  з приготовленими моделями, як на даному малюнку ( в квадратах зі сторонами a і b розташовані вирізані квадрати )

Завдання учням: перевірити  твердження (1).

 Для цього їм потрібно квадрати, які розташовані на катетах,  розташувати на квадраті, який побудований на гіпотенузі трикутника, так, щоб вони повністю його накрили.

Висновок: очевидно, що площа квадрата, побудованого на гіпотенузі прямокутного трикутника, дорівнює сумі площ квадратів, побудованих на катетах трикутника,  тобто, теорема Піфагора доведена.

ІІ. Завдання:  знайти довжини діагоналей квадратів та прямокутників, які лежать на партах. ( учні вимірюють сторони за допомогою лінійки та проводять обчислення у зошитах.)

 Як бачимо, нерідко ми отримуємо у відповідях  ірраціональні числа:  , .    І постає питання: як знайти іх значення, якщо немає поруч калькулятора?  Тому, пропоную послухати учнів, які покажуть два методи знаходження наближених значень таких чисел: алгебраїчний та геометричний.

Два учні виступають з методами знаходження  наближених значень ірраціональних чисел( , , , і т. д.) :

1-й учень показує метод знаходження середнього арифметичного чисел, які ми знаходимо підбором: позначимо = х, тоді за означенням квадратного кореня х² =2.  Рівняння х² =2 поділимо на х. Отримаємо х = . Отже підбираємо число, яке при діленні на нього числа 2 отримаємо те ж саме число. Нехай це число – 1,5.    Тоді маємо:                         

                      2 0 1,5

                      15 1, 33.               Отже, 1,5 ≠ 1,33.

                         50

                          45

                             50

                             45

Знайдемо середнє арифметичне : (1,5 + 1, 33) :2=1, 415.

 

Виконуємо ті ж самі дії:  2: 1,415                               2 000   1,415,

                                                                                        14 15  1,413

                                                                                          5 8 50

                                                                                          5 6 60

                                                                                             1 900

                                                                                             1 415

                                                                                                4850

                                                                                                4245

Ітак, з точністю до десятих ми отримали таку ж частку, як і дільник, тому маємо:  ≈ 1,4.  Якщо потрібна більша точність виконуємо ту ж саму послідовність дій : (1,415 +1,413):2 = 1,414 і т. д.

 

 

2-й учень показує геометричний метод побудови відрізка, який дорівнює значенню .

 

Відкладаємо відрізок, який дорівнює 3 см, на його продовженні відкладаємо відрізок довжиною 1 см : АВ=3см, АС = 1см. З точки А проводимо перпендикуляр до відрізка АВ і  будуємо коло з діаметром СВ і центром  на ньому. Отже, відрізок АК = ( доведення за допомогою формули для знаходження висоти прямокутного трикутника, проведеного до гіпотенузи:

 h = , де     - проекції катетів на гіпотенузу.

 

                                            К

                     

 

 

                                    С   1см А        3см           В

 

 

 

ІІІ. Розв’язування прикладних задач на застосування теореми Піфагора. (Учні класу об'єднуються в три групи  по рядам. Розв'язування задач у групах.)

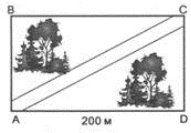     Задача 1 (група 1). Парк має форму прямокутника. Довжина однієї з його сторін дорівнює 200 м, а площа — 72 000 м². Яка довжина головної алеї парку, що проходить по його діагоналі (рис. ).

 

Розв’зання

                               м.                                                                                            

     Відповідь. 411,83 м.

 

     Задача2 (група 2). Космонавт під час польоту знаходиться на відстані

327 км над землею. На якій відстані від корабля знаходились у цей час найбільш віддалені від нього видимі ділянки поверхні Землі (рис. )?

 (Радіус Землі ≈ 6400 км.)

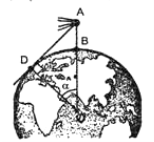
Розв’язання

АО=АВ+ВО=327+6400=6727 (км).

 (км).

     Відповідь. 2071,84 км.

 

     Задача 3 (група 3). Діаметр колоди дорівнює 12 см. Чи можна з цієї колоди витесати квадратний брус із ребром:

а) 10 см; б) 8 см?

Розв'язання

Розглянемо рис.

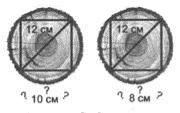
  Рис. 8

а)     d =   =    ≈ 14,14 см  > 12 см, отже не можна.

б)   d =   =    ≈ 11,31 см < 12  см, можна.

     Відповідь. а) Ні; б) так.

 

9. Домашнє завдання творче:

  1. Складіть рекламу кореню.

  2.Придумайте  прикладну задачу на теорему Піфагора.

І рівень №390(2,3), №402(2)

ІІ рівень №390(5,6), №402(4)

ІІІ рівень№398(3), №412(1, 3)

Запам’ятайте слова  «Розвивайся  сам, інакше  почнуть  розвиватися комплекси».

А також заповіді Піфагора:

• Роблячи велике, не обіцяй великого.
• Які б не були короткі слова  «так» та «ні», все ж вони вимагають найсерйознішого роздуму.
• Не роби нічого ганебного ні у присутності інших, ні потайки.
• Першим твоїм законом має бути повага до самого собе!
• Не закривай око, коли хочеш спати, не розібравши усіх своїх вчинків за минулий день.
• По торній дорозі не ходи.

 10.Підсумок уроку.

На дошці дерево Піфагора:

прикрасьте його яблуками червоного кольору, якщо вам  було цікаво, пізнавально та сподобався урок; а якщо на уроці вам було незручно, нецікаво – оберіть яблука зеленого кольору.

11. Виставлення оцінок.