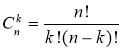Конспект+Презентація+Вказівки для самост.вивчення на тему "Елементи комбінаторики"
- Елементи комбінаторики.docx docx
- комбінаторики.ppt ppt
- . самост.вивч.docx docx
«Три шляхи ведуть до знання.
шлях роздумів - найблагородніший,
шлях наслідування - найлегший,
шлях досвіду - самий гіркий ».
КОНФУЦІЙ
Тема заняття: Елементи комбінаторики
Мета заняття:
навчальна:
- дати означення факторіала та основних понять комбінаторики перестановки, розміщення, комбінації; пояснити комбінаторні правила суми та добутку;
- сформувати вміння знаходити значення і перетворювати вирази з факторіалами;
- використовувати формули комбінаторики для розв'язування найпростіші комбінаторні задач;
- показати практичне використання формул комбінаторики.
виховна:
- формувати інтерес до предмету, наполегливість в досягненні мети і зацікавленості в кінцевих результатах праці;
- виховувати почуття колективізму, взаємодопомоги, підтримки, відповідальності, самостійності, вміння слухати і вступати в діалог, брати участь в колективному обговоренні проблем, будувати продуктивну взаємодію;
розвиваюча:
- розвивати у студентів творчу уяву, пам'ять, увагу;
- розвивати розумову діяльність: вміння аналізувати, узагальнювати досліджувані факти, виділяти і порівнювати суттєві ознаки
Вид заняття: інтерактивна багатоцільова лекція
Форми та методи роботи: робота в групах, метод «перевернутий клас», комп’ютерне тестування.
Забезпечення заняття
|
Наочні посібники |
презентація |
|
Роздатковий матеріал |
Папір А4, фломастери, завдання для роботи в групах, картка великих чисел, аркуші для виставлення рейтингових балів. |
|
ТЗН |
Комп’ютер, Мультимедійний пристрій, калькулятори. |
|
Навчальні місця |
Для групового навчання |
|
Література |
Методична розробка для самостійного вивчення поняття факторіал. А.Г.Мерзляк, Д.А.Номіровський, В.Б.Полонський, М.С.Якір. Алгебра і початки аналізу. Підручник для 11 класу загальноосвітніх навчальних закладів. Академічний рівень. Х.: Гімназія, 2010 |
|
Інтернет ресурси |
https://uk.wikipedia.org/wiki /Комбінаторика |
ХІД ЗАНЯТТЯ
1. Організаційна частина.
Підготовка групи до навчання
- Привітання студентів
- Перевірка присутності студентів.
- Виявлення рівня підготовки студентів до заняття.
- Вступне слово викладача.
- Актуалізація опорних знань
- Відповіді на запитання студентів,
- Перевірка домашнього завдання
- Прокоментувати виконання 1-2 завданнь
Запитання студентам
- Дайте означення ймовірності
- Яку подію називаємо випадковою?
- Що ви розумієте під поняттям кількість усіх елементарних подій?
- Які числа називаємо простими?
Які числа діляться на 5?
- Мотивація навчальної діяльності
На минулій парі ми розглядали ймовірність подій, для яких нескладно було обчислити п і т. Проте, при розв’язуванні багатьох задач знаходження кількості всіх та сприятливих подій потребують спеціальних знань. На практиці часто доводиться відповідати на запитання: скількома способами можна виконати певне завдання. наприклад, сл_2_
- скількома способами можна скласти розклад занять на день,
- скількома способами можна поєднати одяг нашого гардеробу,
- скількома способами скласти меню,
- скількома способами провести спортивні змагання і т.д..
Майже щодня кожному з нас доводиться комбінувати речі з власного гардероба, вирішувати, що вдягнути на ту чи іншу подію сл_3
В таких задачах йде мова про комбінування об'єктів і їх називають комбінаторними задачами, а розділ математики, в якому вивчаються питання про те, скільки різних комбінацій, що відповідають тим чи іншим умовам можна скласти із заданих об'єктів, називається комбінаторикою . сл_4_5
В наш час комбінаторні задачі приходиться розв'язувати фізикам, хімікам, біологам, економістам, спеціалістам самих різних професій сл.6
Широко застосовується комбінаторика у художньому конструюванні виробів– це прийоми знаходження різних поєднань, перестановок, розміщень даних елементів у певному порядку. Сл.7
- Повідомлення теми, мети та завдань заняття
Сьогодні навчимось розв’язувати комбінаторні задачі і будемо працювати за таким планом Сл.8
- Факторіал.
- Множини. Основні поняття. Впорядковані множини
- Перестановки
- Розміщення
- Комбінації
- Сприйняття й засвоєння студентами навчального матеріалу
1.Факторіал Сл.9
Поняття факторіал ви мали опрацювати дома. Перевіримо, чи вдалось Вам розібратись із дією, що позначається знаком оклику у математиці. Вам потрібно було вивчити означення, виконати приклади і з’ясувати, як знаходиться факторіал на калькуляторі. Я буду ставити питання , а Ви відповідаєте.
Отже, Сл.7
|
1.Що таке факторіал.
|
Факторіал — це добуток послідовних натуральних чисел |
|
Які числа називаються натуральними |
Натуральними називаються числа, які використовують при лічбі |
|
Яке найменше (найбільше) число належить множині натуральних чисел |
Найменше - 1 найбільшого не існує |
|
2. Як позначається факторіал. |
п! |
|
3. Що означає п! |
п!= 1 ∙ 2 ∙ 3 ∙ ... ∙ n |
|
4.Обчисліть 5! 6! 4!
|
5! = 120; 6! = 720 4! = 1 ∙ 2 ∙ 3 ∙ 4 = 3! ∙ 4 = 24. |
|
5.Як розписати 9! через 8! 6! Через 5! 100! через 99! |
9! = 8! ∙ 9 100! = 99! ∙ 100 |
|
Розпишіть k! через (k-1)! (k+1)! через k! |
k! = (k-1)! ∙ k (k+1)! = k! ∙(k+1) |
|
Як ви поділили k! На (k-1)! |
k! / (k-1)!= (k-1)! ∙ k /(k-1)!= k |
|
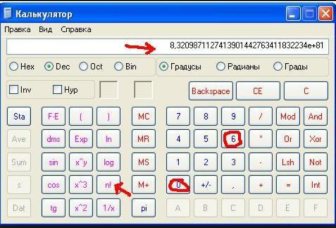
Чи знайшли ви факторіали на калькуляторі 19!, 30! |
19!= 121 645 100 408 832 000> 121квадрильйонa 30!= 2,6 525 285 981 219 105 863 630 848 e+32 ≈ 265 нонільйонів |
- Множини. (елемент множини, види множин, позначення множин). Сл.10
Пригадаємо основні поняття, що стосуються множин:
Що ми називаємо множиною?
Що називаємо підмножиною?
Як поділяються множини в залежності від кількості елементів?
Розв'язуючи комбінаторні задачі, розглядають скінченні множини, утворені з елементів будь-якої природи, та їх підмножини. Залежно від умови задачі розглядаються множини, у яких не є істотним порядок елементів і множини, у яких істотним є або порядок елементів, або їх склад, або і те і те одночасно. Такі скінченні множини мають певну назву.
Множина, кожному елементу якої поставлений у відповідність певний номер, т.б. важливо в якому порядку розташовані елементи, називається впорядкованою.
Уважно подивіться на слайд 11 і назвіть впорядковані і невпорядкі овані множини (впорядковані-розклад уроків, розподіл призових місць. Сл. 11
3.Перестановки
Будь-яка впорядкована множина, яка складається з n елементів, називається перестановкою з n елементів і позначається Рn. Сл.12 Таким чином, перестановки з n елементів відрізняються між собою лише порядком розташування елементів.
Робота в групах Сл.13-14
на аркушах ПЕРЕСТАНОВКИ Робота №1
Студенти виконують завдання передбачені для кожної із груп
|
|
Завдання |
|
1 група |
|
|
2 група |
|
|
3 група |
|
Число перестановок з n елементів дорівнює добутку всіх натуральних чисел від 1 до п, тобто п! (читають: єн факторіалів). Сл.15
Рn = п!, п! =1 ∙ 2 ∙ 3 ∙ ... ∙ n
Розв’яжемо задачу Сл.16
У сім'ї 6 осіб, а за столом в кухні 6 стільців. Було вирішено щовечора перед вечерею розсідатися на ці 6 стільців по-новому. Скільки днів члени сім'ї зможуть робити це без повторень?
Розв'язування
P6 = 6! =l · 2 · 3 · 4 · 5 · 6 = 720.
Відповідь: 720 днів, або протягом 2 років.
Робота в групах
Кожній групі потрібно розв’язати свою задачу і записати розв’язок на дошці. Сл.17
1 група.
У класі навчається 10 юнаків. Скількома способами можна їх вишикувати у шеренгу?
2 група.
Скількома способами можна скласти список із 9 прізвищ?
3 група.
Скількома способами можна розкласти 8 різних листів у 8 різних конвертів, якщо в кожний конверт кладеться лише 1 лист?
Подумайте і сформулюйте задачу яка б стосувалась вашої групи або нашого коледжу і в якій би можна було порахувати кількість перестановок і розв'яжіть її. Сл.18
- Розміщення
А скільки k - елементних упорядкованих підмножин можна утворити з n різних елементів, якщо n ![]() k? Такі упорядковані підмножини називають розміщеннями з n елементів по k елементів.
k? Такі упорядковані підмножини називають розміщеннями з n елементів по k елементів.
Будь-яка впорядкована підмножина з k елементів даної n-елементної множини називається розміщенням з n елементів по k, k ≤ n. Сл.19
Робота в групах Сл.20
на аркушах РОЗМІЩЕННЯ Робота №2
|
|
Завдання |
|
1 група |
|
|
2 група |
|
|
3 група |
|
Назвіть число підмножин які ви отримали.
Кількість розміщень з n елементів по k позначається ![]() (читається: "А з ен по ка") і обчислюється за формулою Сл.21
(читається: "А з ен по ка") і обчислюється за формулою Сл.21
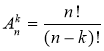
Перевіримо, чи правильно виконали завдання ![]()
Розв’яжемо задачу. Сл.22
10 спортсменів розігрують одну золоту, одну срібну і одну бронзову медалі. Скількома способами ці медалі можуть бути розподілені між спортсменами?
Розв'язування
![]()
Відповідь: 720 способів.
Робота в групах
Кожній групі потрібно розв’язати свою задачу і записати розв’язок на дошці. Сл.23
1 група
В 11 класі вивчається 14 дисциплін . Скількома способами можна скласти розклад занять на п’ятницю, якщо в цей день повинно бути 6 різних уроків?
2 група
Юнак має 10 різних художніх книг. Він хоче подарувати по 1 книзі чотирьом одногрупникам. Скількома способами це можна зробити?
3 група
У класі з 32 учнів для проведення зборів обирають голову, заступника і секретаря. Скількома способами це можна зробити?
Подумайте і сформулюйте задачу яка б стосувалась вашої групи або нашого коледжу і в якій би можна було порахувати кількість розміщень і розв'яжіть її. Сл.24
Запам’ятайте! Розміщення і перестановки обов’язково враховують порядок розташування елементів Сл.25
- Комбінації (Сполуки)
Розміщення - це впорядковані підмножини даної множини. А скільки не-впорядкованих двохелементних підмножин можна скласти з тих самих елементів?
Будь-яка підмножина з k елементів даної множини, яка містить n елементів, називається комбінацією (сполукою) з n елементів по k елементів.
Отже, комбінацією (сполукою) називають будь-яку k - елементну підмножину даної n - елементної множини. Сл.26
Число комбінацій з n елементів по k позначають символом ![]() і обчислюють за формулою
і обчислюють за формулою
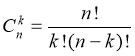 .
.
Наприклад: ![]()
Робота в групах Сл.27
на аркушах КОМБІНАЦІЇ Робота №3
|
|
Завдання однакове для всіх груп |
|
1 група |
|
|
2 група |
|
|
3 група |
Скільки вийшло прямих? 10. Перевіримо обчислення.
![]()
Розв’яжемо задачу. Сл.28
В лотереї «Мегалот» необхідно закреслити 6 цифр з 42. Скількома способами це можна зробити?
Розв’язання :
В цій задачі n=42, а k =6, скористаємося формулою :
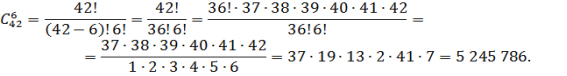
Відповідь: 5 245 786 способів
Робота в групах
Кожній групі потрібно розв’язати свою задачу і записати розв’язок на дошці. Сл.29
1 група.
Для проведення іспиту створюється комісія із двох викладачів. Скільки різних комісій можна скласти із п’яти викладачів?
2 група.
Із 20 учнів треба виділити 6 для чергування. Скількома способами це можна зробити?
3 група.
На полиці є 35 книжок. Скількома способами можна вибрати дві із них?
Подумайте і сформулюйте задачу яка б стосувалась вашої групи або нашого коледжу і в якій би можна було порахувати кількість комбінацій і розв'яжіть її. Сл.30
Висновки: Сл.31
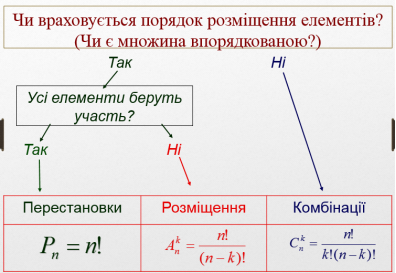
- У випадку перестановок беруться всі елементи і змінюється тільки їх розташування.
- У випадку розміщення береться тільки частина елементів і важливо розміщення елементів один відносно одного.
- У випадку комбінації береться тільки частина елементів і не має значення розміщення елементів один відносно одного.
Як вибираємо формулу? На що звертаємо увагу? Сл.32
Якщо все зрозуміло, розв’яжемо задачі з підручника (за наявності часу) Сл.33
6. Закріплення нового навчального матеріалу (Тести на слайдах)
Перейдемо до розв’язування задач формату ЗНО. Сл.34


Перевір себе ( інтерактивні тести).Робота з комп’ютерними тестами
Перевіримо, чи все зрозуміло з сьогоднішньої теми заняття. Виконайте наступні тести. Сл.35-39
7. Підсумок заняття: узагальнення вивченого матеріалу, характеристика роботи групи на занятті.
- Узагальнення вивченого матеріалу
- Проаналізувати активність студентів на занятті.
- Рівень засвоєння теми.
Характеристика роботи студентів на занятті.
8. Постановка домашнього завдання .
1
Методичні вказівки
до вивчення поняття «факторіал»
Для вивчення поняття «факторіал» опрацюйте теоретичний матеріал, розв’яжіть запропоновані завдання та дайте відповіді на питання для самоконтролю.
- Теоретичний матеріал
Факторіал — це добуток послідовних натуральних чисел. тобто
п! = 1 ∙ 2 ∙ 3 ∙ ... ∙ n. (читається п–факторіал)
Наприклад : 1! = 1;
2! = 1 ∙ 2 = 2;
3! = 1 ∙ 2 ∙ 3 = 6;
4! = 1 ∙ 2 ∙ 3 ∙ 4 = 3! ∙ 4 = 24.
Приймають, що 0! = 1.
Термін «факторіал» походить від англійського слова «фактор» — множник.
Більший факторіал можна розписати через менший. Наприклад :
5! = 1 ∙ 2 ∙ 3 ∙ 4 ∙ 5 = 4! ∙ 5 або
5! = 1 ∙ 2 ∙ 3 ∙ 4 ∙ 5 = 3! ∙ 4 ∙ 5
п! = 1 ∙ 2 ∙ 3 ∙ ... ∙ (п–1) ∙ п.= (п–1)! ∙ п
п! = 1 ∙ 2 ∙ 3 ∙ ... ∙ (п–2) ∙ (п–1) ∙ п.= (п–2)! ∙ (п–1) ∙ п
тобто, n!=n(n−1)!=n(n−1)(n−2)!=n(n−1)(n−2)(n−3)! і т.д
Приклад 1. Обчислити 5!+6!
Розв'язання
Обчислити даний вираз можна двома способами.
5!+6!=120+720=840 або 5!+6!= 5!+5! ∙ 6=5!(1+6)=120 ∙ 7=840
Приклад 2. Обчислити ![]() .
.
Розв'язання
Розписуємо більший факторіал 102! через менший 100!, скорочуємо на 100!. У дробі рівні факторіали можна скорочувати.
![]() .
.
Приклад 3. Спростити: ![]() .
.
Розв'язання
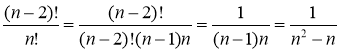 .
.
2. Розв’яжіть наступні завдання:
2.1 Обчисліть:
а) 8!+9!; б) 9!–8!; в); ![]() г).
г). ![]()
2.2. Скоротіть дріб:
a); ![]() б)
б) ![]()
3. Ознайомтесь із знаходженням факторіалу на калькуляторі.
Обчисліть на калькуляторі 19!, 30!
4. Ознайомтесь із історією розвитку комбінаторики.
Сайт http://svitppt.com.ua/matematika/istoriya-rozvitku-kombinatoriki.html
Питання для самоконтролю:
- Дайте означення факторіалу.
- За якою формулою обчислюється факторіал.
- Чи можна розписати більший факторіал через менший. Як це зробити.
- Чи можна розписати менший факторіал через більший.


про публікацію авторської розробки
Додати розробку