Славутський навчально-виховний комплекс

« Спеціалізована школа І-ІІІ ступенів, ліцей « Успіх »

 

 

Конспект   STEM - уроку       на тему

« Застосування засобів геометрії для підвищення енергоефективності будинків

(Розв‘язування задач на обчислення об’ємів та площ поверхонь геометричних тіл) »

 

 

розробила

вчитель математики

  Шелестюк А.О.

 

 

 

2019 – 2020 н.р.

 

Тема уроку.

« Застосування засобів геометрії для підвищення енергоефективності будинків

(Розв‘язування задач на обчислення об’ємів та площ поверхонь геометричних тіл) »

Мета уроку.

Формування компетентностей:

предметна компетентність:

навчальна  - повторити теоретичний матеріал з теми «Об’єми та площі поверхонь геометричних тіл», узагальнити, систематизувати і поглибити знання учнів про об’єми геометричних тіл при розв’язуванні практичних задач;

розвивальна - розвивати вміння творчо мислити,  працювати самостійно, робити висновки;

виховна - виховувати самостійність, як засіб інтелектуального розвитку, працьовитість, кмітливість, інтерес до нових знань і прагнення їх набути;

Тип уроку: вдосконалення вмінь і навичок при розв’язку задач

ключові компетентності:

уміння вчитися впродовж життя — оцінювати результати своєї навчальної  ді­яльності;

ініціативність і підприємливість — використовувати критерії раціональності, практичності, ефективності та точності з метою вибору найкращого рішення;

основні компетентності у природничих науках і технологіях — будувати та до­сліджувати математичні моделі процесів.

Тип уроку: урок узагальнення та систематизації знань.

Обладнання та наочність: комп’ютер, проектор, картки з текстовими завданнями.

Хід уроку

І. ОРГАНІЗАЦІЙНИЙ ЕТАП

ІІ. Повідомлення теми й мети уроку.

ІІІ. Мотивація навчальної діяльності.
   Антична мудрість стверджує «Знання – це сила». На мою думку, знання – це одна із сходинок до успіху в майбутньому. І сьогодні ми будемо плідно працювати, щоб досягнути мети. Отож метою нашого уроку є узагальнення та систематизація знань, умінь та навичок з теми «Площі поверхонь та об’єми геометричних тіл».  Тому сьогодні на уроці ми будемо розв’язувати задачі з геометрії прикладного характеру, за допомогою яких розкриваються можливості реалізації зв’язку математичної та професійної підготовки учнів.

 Ви стоїте на порозі закінчення школи. Здавалось би, що після школи математика ніде не пригодиться. На жаль! Тут приходиться використовувати математику ще більше.

Практичні задачі геометричного змісту ─ найактуальніша тема для сьогоднішніх школярів. Ці завдання сприяють застосуванню отриманих знань в реальному житті.

  Уміння вирішувати такі завдання допоможе адаптуватися в суспільстві.

ІV. Відтворення та коригування опорних знань
АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ

1. Інтерактивна вправа «Мікрофон»

1. Дайте означення геометричного тіла
2. Дайте означення призми. Назвіть її елементи
3. Назвіть види призм
4. Дайте означення піраміди. Назвіть її елементи
5. Назвіть види пірамід
6. Дайте означення тіл обертання

 

2. Інтерактивна вправа « Геометричні тіла та їх назви»

         https://learningapps.org/1629214

 

 

 

 

 

 

 

 

 

 

 

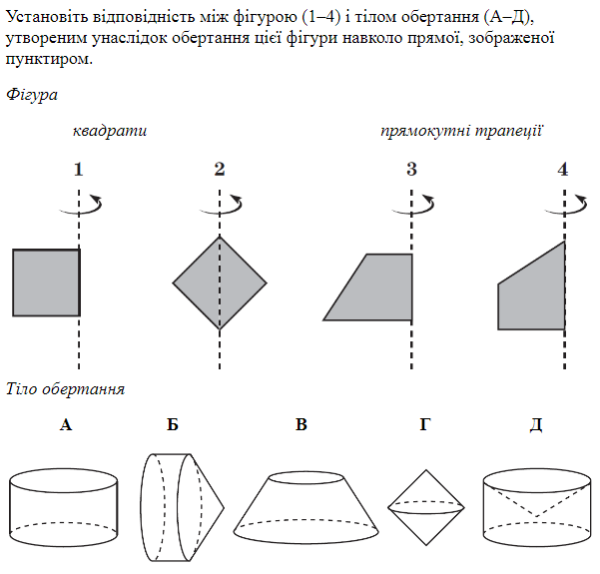
     3. Інтерактивна вправа « Формат ЗНО»

 

	А	Б	В	Г	Д
1
2
3
4

Відповідь: 1-А,   2 –Г,  3 –В, 4-Б

 

 

 

 

VІ. Узагальнення та систематизація понять.

Реалізація накрізної лінії   «Екологічна безпека та сталий розвиток»

 

1. Інтерактивна вправа «Взнай слово»

Розв’яжіть прикладні задачі

 

Задача 1.

Скільки повних порцій супу міститься в каструлі, яка має форму циліндра, висота якого 40 см, а діаметр 0,3 м. Відомо, що одна порція містить 0,25 л супу.

Дано: V_п =0,25л=250см³;

h=40cм; R=15cм.

Знайти: n – кількість порцій.

     Розв‘язання:

     V = R²H = 3,14 ·15² ·40 = 28260 ( см²), (порцій).

 

                  

Відповідь: 113 порцій.

 

Задача 2.    Циліндрична  димова труба  діаметром

65 см має висоту 18 м. скільки жерсті треба для її виготовлення, якщо на заклепку іде 10% матеріалу?

 

Дано: циліндр, d=65см,   H = 18 м  = 18000см,

 Знайти: S_б

                                         Розв’язання:

              S_б =dH = · 65 · 1800 = 117000 см² =  11, 7 м².

          Але це становить 90% від усієї жерсті. м²

                                          Відповідь: жерсті потрібно взяти 40,8 м²

Задача 3

Картоплю насипали в купу конічної форми. Довжина кола основи купи 12 м, твірна -3м.Скільки тонн картоплі знаходиться в купі? Маса 1м³ картоплі 800 кг.

Дано:    конус, С = 12 м, l = 3м.

Знайти:     V_к , m.

Розв’язання:

 

C = 2R.    R = м.

З  трикутника ОВS за теоремою Піфагора: м.

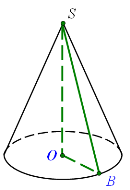Об’єм шукаємо за формулою:

м³

 

m = 2,98 · 800 = 2384 кг.

 

Відповідь: 2384 кг картоплі в купі.

 

Задача 4.

Скільки мішків аміачної селітри можна помістити в склад розмірами 20м х 9м х 4м, якщо мішок селітри можна прийняти (з певною похибкою) за прямокутний паралелепіпед розмірами 90смх 5смх25см? (На щілини між мішками і центральний прохід виділяється 30% об’єму складу)

 

Дано:    АВСД – прямокутний паралелепіпед, з вимірами  20м х 9м х 4м,

А₁В₁С₁Д₁ – прямокутний паралелепіпед з вимірами 90смх 5см х 25см.

Знайти: кількість мішків, n.

Розв’язання:

V₁ = abc = 20 · 9 · 4 = 720 м³.

Перетворимо см у м:

90 см = 0,9м, 5 см = 0,05м, 25 см = 0,25 м.

V₂ = a₂b₂c₂ = 0.9 · 0.05 · 0.25 = 0.0113 м³.

30% об’єму складу становить: 720 · 0,3 = 216 м³.

Об’єм складу з урахуванням вичету 30%: 720 – 216 = 504 м³.

n = 504 : 0,0113 44601

Відповідь: 44601 мішок можна помістити у такий склад.

 

Задача 5.

Фермер вирішив побудувати колодязь циліндричної форми, що має в діаметрі 135 см., А глибину 380 см., Який треба викласти цеглою. Скільки штук цегли йому потрібно купити, якщо розмір цегли 25 X 12 X 6,5 см.

Розв’язання: Довжина кола, діаметр якої менше діаметра колодязя на подвоєну ширину цегли, дорівнює рd ≈ 351 см.

Довжину кола ділимо на довжину цегли, отримуємо 351: 25 ≈ 14 цегли укладено  в   один ряд. Таких  рядів буде  380: 6,5 ≈ 59. Отже,  потрібно  цегли   

14 · 59 = 826 штук.

Відповідь: потрібно цегли 826 штук.

Задача 6.

Для поливу висячих садів Семіраміди щодня тисячі рабів качали воду з глибоких колодязів на верхні тераси, а вже звідти по численних каналах вода стікала на нижні тераси. Визначте якою була загальна глибина колодязів, якщо відомо, що радіус цих колодязів 1 м і щодня з них викачували 3 140 м³ води.

Дано: циліндр, R=12 м,   V=3140м,

                                                                         Знайти: h

Розв’язання:

Vцил.=R² h,    h = = 1000 м.

                                        Відповідь:  1000 м

Задача 7.

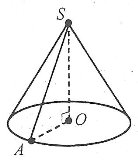
 Конусоподібний намет висотою 3,5м і діаметром основи 4м покрито тканиною. Скільки тканини пішло на намет?

Дано: конус, SO = H = 3.5м,  d = 4м.

Знайти:  S_б

Розв’язання:   S_б. =

З трикутника АОS: кут О = 90°, за т. Піфагора:

S_б = 3,14 · 2 · 4,03 =25,3 м².

Відповідь: 25,3 м² тканини пішло на намет.

 

 

п	н	г	е	о	р	е	м	я	і
418	40,8	826	113	254	44601	2384	115	25,3	1000

Відповідь: енергія

1. Інтерактивна вправа «Математична цікавинка»

Принципи формування архітектури енергоефективних будинків

  Однією із важливих проблем  сучасності є питання про раціональне використання обмежених ресурсів, зокрема нафти, природного газу, вугілля. Вона набуває своєї значимості і в екологічному, і в економічному питаннях. Споживання згаданих вище ресурсів зараз відбувається у великих об’ємах, тому, за прогнозами вчених, вони можуть вичерпатися вже на початку XXII століття. Отже, актуальними є питання про раціональне використання  нафти, природного газу, вугілля та енергозбереження. Питання про оптимізацію форми будинків є одним із важливих у підвищенні енергоефективності, оскільки вона є основою для подальшої зміни її архітектури  з метою вдосконалення.

      За проектом архітекторів Ніколаса та Ендрю Ісаків у 1972 році був побудований перший енергоефективний будинок. Він був кубічної форми, тому мав мінімальну площу зовнішніх стін, а площа скління становила всього 10%. Таким чином були знижені втрати тепла. Пізніше подібне енергоефективне будівництво з’явилося у Фінляндії під назвою Econo-house. Сьогодні багато енергоефективних будинків побудовано у Норвегії, Іспанії, Данії, Японії. Зараз найбільше приділяється уваги їх формам. У даному питанні лідерство належить сучасному видатному британському архітектору серу Норману Фостеру.  У Лондоні він побудував споруду «Сіті-хол»

, яка розташована на набережній Темзи неподалік від Тауерського мосту та має форму схожу на яйце, тоненько нарізане скибочками. Архітектор пояснює таку форму своєї будівлі - економією електроенергії. Покриття «Сіті-хол» складається з 3844 скляних панелей, кожна з яких вирізувалася спеціальним лазарем, тому є унікальною. Всередині будівлі є гвинтові сходи, які ведуть до десятого поверху.

   Сьогодні багато житлових будинків України, за результатами проведеного аналізу, не відповідають вимогам енергозбереження по причинах: недосконалості їх архітектур, використання в будівництві застарілих типів інженерних систем та неефективних конструкторських матеріалів. Вони потребують 25 – 30% палива від загальної кількості, яку витрачає держава щорічно.  В Україні за один опалювальний період на 1 млн. м² житлової площі витрачається приблизно 55000 т натурального палива, що у 2-3 рази більше ніж у Швеції та у 1,5 рази – ніж у США. Причиною такого є незначне використання альтернативних джерел енергії та впровадження енергозберігаючих технологій.

  Говорячи про зменшення витрат на опалювання будинків, ми думаємо про утеплення стін, і це вірно, оскільки не може будинок бути енергоефективним, коли  його конструкції «гріють» повітря. Одним із способів зменшення витрат є вибір раціональної ( оптимальної ) форми будівлі. При проектуванні часто є неможливим використання раціональних пропорцій будинку тому, що це пов’язано із використанням  уніфікованих розмірів конструкційних елементів, розмірів прогонів, функцій будинку, висот поверхів, можливістю підбору пропорцій з точки зору візуальної виразності тощо. Тому постає питання про розв’язування задачі на знаходження оптимальних форм будинку.

  Розглянемо концепцію визначення раціональних пропорцій житлових будинків. Вона полягає в тому, що існує розроблений комплекс геометричних моделей, які дозволяють архітектору- проектувальникові в інтерактивному діалоговому режимі проектувальник-ЕОМ знаходити:

раціональні пропорції будинку;

оптимальні пропорції будинку ( тепловтрати на заданий рівень процентів перевищують раціональні);

визначити інтервал можливих пропорцій будинку тощо.

 

VІІ. Засвоєння провідних ідей і теорій на основі широкої систематизації.

STEM - формат

Інтерактивна вправа «Вмій застосувати»

Розв’язування задач в групах

  Солара І. вважає, що необхідно робити форму будинку компактніше, з мінімальним відношенням площі зовнішніх огороджень до житлової площі будинку. Розглянувши такі види геометричних фігур, як: кулю, квадрат, витягнутий прямокутник, він зробив висновок, що ідеальною формою будинку буде куля, але  оскільки їх не зручно будувати, тому оптимальною формою є квадрат. З точки зору зниження витрат на опалення будинку, найгіршою є будівля у вигляді високої вежі або витягнутої  з порізаними фасадами. Ми розширимо перелік геометричних фігур, зробимо свої дослідження та одержимо результати, які проаналізуємо.

  Розрахунки проведено для умовно взятої території забудови площею 200 м² ( 20 х 10 )  та висотою 10 м.

  Учні поділяються на 5 груп, кожна з яких проведить розрахунки для геометричних тіл: паралелепіпеда, чотирикутної піраміди, циліндра, кулі, конуса.

1) Паралелепіпед.

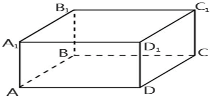Рис.1

Нехай ABCDA₁ B₁ C₁ D₁ – заданий паралелепіпед, в основі якого лежить прямокутник ABCD. Паралелепіпед має виміри  a, b, с

( висота, довжина, ширина )

        c = АВ = 10 м,  b = AD = 20 м,   a = АА₁ = 10 м.  

V = abc,  

V_парал. = 10·20·10 = 2000 ( м³).

S_{бічна пов.} = 2 (S₁  + S₂), S_{біч.пов} = 2 ( 20 ·10 + 10 · 10 ) = 600 ( м²).

S _основи = bc;   S _основи = 20 · 10 = 200 ( м²).

S_{повна пов.} = S_{бічна пов.} + 2 S _основи;  S_{повна пов.} = 600 + 2· 200 = 1000 ( м²).

Обчислимо відношення 

2) Чотирикутна піраміда.

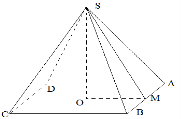Рис.2

Нехай SABCD – задана піраміда, в основі якої лежить  прямокутник ABCD, AB = CD = 10 м,   BC = AD = 20 м. 

Бічні ребра піраміди  SC = SA = SD = SB. 

Висота SO   (ABC ), OM AB, тоді за теоремою про три перпендикуляри  SM AB,  SO = 10 м.

S _основи ·H;    S _основи = AB · BC:   S _основи = 10 · 20 = 200 ( м²).

·200 · 10 = ( м³).

S_{бічна пов.} = 2 (S₁  + S₂), де S₁ = , S₂ = .

Оскільки AC, BD – діагоналі прямокутника, то за їх властивостями

AC BD = О,  AО = CО = BО = DО = AC,

для  знаходження AC  розглянемо  , у якого =90⁰,

AB = 10 м,   BC =  20 м, тоді за теоремою Піфагора  ,

(м), отже

AО = CО = BО = DО = · =(м).

Розглянемо  , у якого =90⁰,

SO = 10 м,  OB = м, тоді за теоремою Піфагора  ,

(м), отже,

 SC = SA = SD = SB = 15 м.

Розглянемо  , у якого SC =  SB = 15 м, SК СB, СВ = 20 м.

                         S

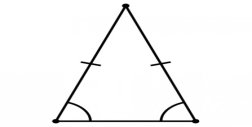Рис.3

C K B

Оскільки - рівнобедрений, то за йoго властивостями

СК = КВ = СВ, СК = КВ = ·20 = 10 ( м).

Розглянемо  , у якого =90⁰,

SВ = 15 м,  КB = 10 м, тоді за наслідком з теореми Піфагора  ,

(м), отже, обчислимо

S₁ = , , ( м²).

Розглянемо  , у якого SA =  SB = 15 м, SM AB, AВ = 10 м.

                       

 

 

 

 

 

                         S

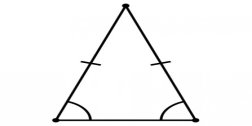Рис.4

B M A

Оскільки - рівнобедрений, то за йoго властивостями

BM = MA = AВ, BM = MA = ·10 = 5 ( м).

Розглянемо  , у якого =90⁰,

SВ = 15 м,  MB = 5 м, тоді за наслідком з теореми Піфагора  ,

(м), отже обчислимо

S₂ = . , ( м²).

Отже,  обчислимо

S_{бічна пов.} = 2 (  111,8034 + 70,7107) =2 ·182,5141 = 365,0282 ( м²).

S_{повна пов.} = S_{бічна пов.} +  S _основи;

 S_{повна пов.} = 365,0282  + 200 = 565,0282( м²).

Обчислимо відношення 

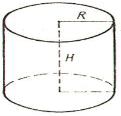3) Циліндр.

               

Рис.5

 

Нехай задано циліндр, у якого H = 10 м, R = 10 м.

; ( м³). 

S_{бічна пов.} = ;  S_{бічна пов.} = ( м²).

  S_{повна пов.} = S_{бічна пов.} +  2S _основи;   S _основи = ;   S _основи = ( м²).

S_{повна пов.} = 628 + 2·314 = 628 + 628 = 1256 ( м²).

Обчислимо відношення 

4)  Куля.

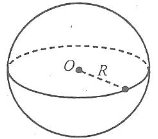Рис.6

Нехай задано кулю, у якої R = 5 м.

;  ( м³). 

S_повна = S_сфери = ;  S_повна = S_сфери = ( м²).

 

Обчислимо відношення 

 

 

 

 

 

5)  Конус.

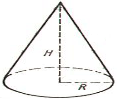Рис.7

  Нехай задано конус, у якого H = 10 м, R = 10 м.

; ( м³). 

S_{бічна пов.} = ;  де твірна.

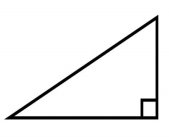  Для обчислення твірної  розглянемо прямокутний трикутник, у якого катети R та H, а гіпотенуза - .

 

 

H     Рис.8

                    R

H = 10 м, R = 10 м, тоді за теоремою Піфагора  ,

(м), отже,

S_{бічна пов.} = ( м²).  

 S_{повна пов.} = S_{бічна пов.} +  S _основи;   S _основи = ;   S _основи = ( м²).

S_{повна пов.} = 444,063 + 314 = 758,063 ( м²).

Обчислимо відношення 

Запишемо одержані результати у таблицю 1.

 

 

 

№	Форма будинку	Об’єм ( V ), м3	Площа повної поверхні (Sповна), м2	Співвідношення
1	Паралелепіпед	2000	1000	0,5
2	Піраміда	666,(6)	565,0282	0,85
3	Циліндр	3140	1256	0,4
4	Куля	523,(3)	314	0,6
5	Конус	1046,(6)	758,063	0,7

  За результатами нашого дослідження можна зробити висновок, що найбільш вдалою формою для будування будинку висотою 10 м є циліндр, куля, паралелепіпед, оскільки їх відношення площі до об’єму є найменші з одержаних у таблиці результатів.

  Проведемо розрахунки для умовно взятої території забудови площею 200 м² ( 20 х 10 )  та висотою 3 м.

Запишемо одержані результати у таблицю 2.

№	Форма будинку	Об’єм ( V ), м3	Площа повної поверхні (Sповна ), м2	Співвідношення
1	Паралелепіпед	600	580	0,9(6)
2	Піраміда	200	421,02	2,1
3	Циліндр	942	816,4	0,87
4	Куля	14,13	28,26	2
5	Конус	314	412,34	1,3

 

  За результатами нашого дослідження можна зробити висновок, що найбільш вдалою формою для будування будинку із висотою 3 м є  циліндр та паралелепіпед, оскільки їх відношення площі до об’єму є найменші з одержаних у таблиці результатів.

 Отже при збільшенні висоти будинку відбуваються зміни його пропорцій, тобто перелік та кількість фігур раціональних для будування можуть змінюватися та варіюватися. Таким чином, підвищення енергоефективності будинків залежить не лише від їх форм, але також від співвідношення площі зовнішніх огороджень до об’єму.

VІІІ. ПІДБИТТЯ ПІДСУМКІВ УРОКУ, РЕФЛЕКСІЯ

Відеоролик «Унікальний екокномний будинок-купол, що збудував українець»

www.youtube.com/watch?v=Bi1H4YL9Vb

I

IX. ДОМАШНЄ ЗАВДАННЯ

Реалізація накрізної лінії   «Здоров'я і безпека»

Завдання 1. Розв’язати прикладну задачу

Вважають, що шкідливо залишати на ніч квіти в кімнаті, тому що вони поглинають О₂ , необхідний для дихання людини. Щоб, довести, чи вірна ця думка, обчисліть, до якої величини знизиться вміст кисню у кімнаті розміром 5 м × 3м × 3м за 10 годин внаслідок дихання рослин масою 4 кг і середньою інтенсивність дихання 12 мл О₂ на 1г за добу (умови нормальні). Початковий вміст кисню 21%.

 Завдання 2. Зробити одну із моделей геометричного тіла та обчислити

.

 

3.Додаткове завдання.

Побудова енергоефективних будинків в Україні

  В Ужгороді Валерій Самойлов сам спроектував та побудував енергоефективний будинок у вигляді півсфери.

  Ідея звести незвичайне, енергоощадне та недороге житло з’явилась у нього сім років тому. Не маючи архітектурної освіти, він за допомогою спеціальної програми навчився проектувати 3-D моделі на комп’ютері. Каркас купольної будівлі складається з дерев’яних деталей, які з’єднуються між собою спеціальними металевими кріпленнями. У якості утеплювача виступає ековата, яка добре тримає тепло. Зовні дім здається маленьким, однак усередині багато світла, затишно та, на диво, просторо, хоча у будинку лише одна кімната. Стіни у куполі рівні до висоти у 80 см, вище – починають звужуватись. Валерій Самойлов опалює будинок дровами. Завдяки сферичній формі приміщення швидко нагрівається і довго тримає температуру на рівні 26 ⁰С.

Переваги купольного будинку:

• Енергоефективність. Купольний будинок має меншу площу тепловіддачі і поліпшену природну конвекційну вентиляцію, тому його простіше і дешевше опалити або остудити.
• Доступність. Вартість будівництва купольного будинку дешевше, ніж будівництво прямокутної будівлі з таким же корисним об'ємом. Завдяки невеликій вазі конструкція не вимагає дорогого фундаменту.
• Висока стійкість до вітрових навантажень, завдяки аеродинамічній формі.
• Висока сейсмічна стійкість. Сферичний купол Фуллера, побудований з трикутних елементів, має дуже рівномірний розподіл навантажень по всій площині каркаса.
• Акустика. У купольном будинку менше чутні зовнішні шуми.
• Вільне планування внутрішніх приміщень, не обмежена колонами і розпірками.
• Естетика і футуристичний зовнішній вигляд.