Конспект уроку - практикуму спецкурсу з геометрії для 10 класу з поглибленим вивченням математики «Стереометрія в типових задачах».

Конспект уроку -  практикуму

спецкурсу з геометрії

для 10 класу з поглибленим вивченням математики

 «Стереометрія в типових задачах».

 

Урок 6 – 7 (2 години)

Тема:  Побудова  перерізів  многогранників  площиною, яка проходить через дану точку  паралельно  даній  площині.

Мета:

- формувати у учнів практичні уміння будувати перерізи многогранників, які проходять через дану точку паралельно даній площині;

- розвивати логічне мислення  та просторову уяву;

- розвивати акуратність виконання креслень;

- виховувати культуру математичних записів.

Тип уроку: Урок-практикум

Хід уроку.

     І. Постановка мети та мотивація навчальної діяльності учнів.

     Вироблення практичних вмінь та навичок в розв’язуванні основних типових задач  та задач більше складних, які засновані на типових задачах по даній темі. Звертається увага на те, що задачі цього типу мають практичну направленість, систематизують знання по темі «Паралельність прямих та площин».

   ІІ.  Актуалізація опорних знань.

      Повторюються означення та ознака паралельності площин, а також теорема: дві паралельні площини перетинаються третьою площиною по паралельним прямим;  спосіб побудови площини, яка проходить через дану точку  паралельно  даній  площині.

   ІІІ. Розв’язування задач.

        Задача 1. На ребрах ВС,  та СС₁ та СD  призми АВСDА₁В₁С₁D₁ дані відповідно точки  М, N, К. Побудуйте переріз призми площинами α₁, α₂, α₃, паралельними  площині М N К, та які проходять через точку:

а) Р, задану на ребрі ВС;

б) L, задану на ребрі DD₁;

в) F , задану на ребрі АА₁

 

 Розв’язується  опорна  задача  №1, а.

  Здійснюється  колективний аналіз розв’язування задачі, учитель показує зразок розв’язування задачі.

Розв’язання

Будуємо переріз призми площиною МNК. Так як площина α₁ проходить

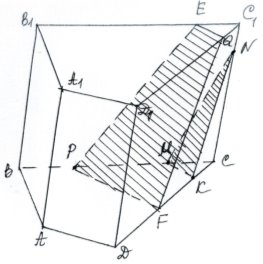                                                               через точку Р , що лежить в площині 

                                                               ВСС₁, то площина α₁ перетинає

                                                               площину ВСС₁ по прямій , що проходить

                                                               через точку Р. Так як  площина α₁

                                                                 паралельна  площині М N К, то сліди

                                                                площини  α₁  та площини  МNК на

                                                                          площині ВСС₁   паралельні.

                                                                       Тому в площині ВСС₁ через точку Р

                                                                проведемо пряму  РЕ║МN.

Міркуючи аналогічно,проведемо в площині АВС через точку Р пряму

РF║МК та в площині DСС₁ через точку F проведемо пряму FQ ║КN.

 З’єднаємо  точку Е з точкою Q. Чотирикутник  РЕQF – шуканий переріз.

      Зауваження. Пряма ЕQ повинна виявитись паралельною прямій РF.

      Запис в зошити.

 

План побудови.

1. Будуємо площину  МNК.
2. (МNК) ∩( ВСС₁) = МN.
3. (МNК) ∩( АВС) = МК.
4. (МNК) ∩( DСС₁) = КN.
5. Проводимо  РЕ║МN,  Рє ( ВСС₁),   РЕ∩ В₁С₁ = Е.
6. Проводимо  РF║МК,  Рє ( АВС),   РF∩DС = F.
7. Проводимо  FQ║КN, Fє ( DСС₁),  FQ∩DС = Q.
8. З’єднуємо Е з  Q.

РЕQF – шуканий переріз.

 

Задачі 1, б та 1, в розв’язуються колективно. При розв’язанні задачі 1, в

учитель  звертає увагу на те, що необхідно побудувати допоміжний переріз.

Розв’язання

Будуємо переріз призми площиною МNК. Так як точка L та пряма КN лежать

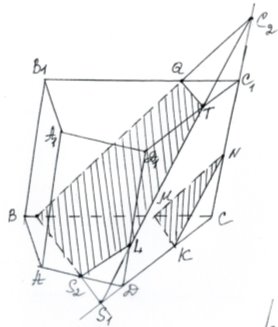                                                                  в одній площині, то ця площина

                                                                  перетинає площину α₂ та площину

                                                                  МNК по паралельним прямим. Тому

                                                                  в площині СDD₁ через точку  L

                                                                  проведемо пряму, паралельну прямій

                                                                  КN. Отримаємо наступні точки Т – на

        S₃                                                          ребрі  С₁D₁,  С₂ – на прямій СС₁,  S₁ –

                                                                  на прямій  СD.

                                                                     Міркуючи аналогічно, проведемо в

                                                        площині АВС через точку S₁ пряму,

                                                        паралельну прямій  МК. Отримуємо

точку S₂  на ребрі  АD та точку S₃ на ребрі  ВС.

   В площині  ВСС₁ проведемо пряму S₃С, яка перетинає ребро В₁С₁ в точці Q.

П’ятикутник  LТQ S₃ S₂ – шуканий переріз. (В зошитах записується план побудови).

Розв’язання                         

 

 

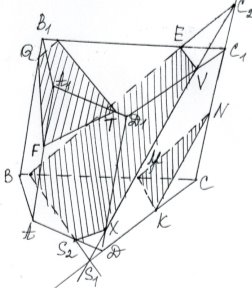в)   Будуємо переріз призми площиною МNК. Оскільки точка  F

                                                     ні з одною  з трьох прямих  МN,  МК

                                                     та  КN не лежить в площині однієї

                                                     грані, то побудуємо спочатку

                                                     допоміжний переріз призми площиною,

                                                                паралельною до площини  МNК, який

                                                                проходить через деяку точку Х. Точку

                                                                Х при цьому задамо в площині такої

                                                                грані призми, яка містить одну з трьох

                                                      вказаних прямих МN,  МК   або КN.

Наприклад,  задамо точку Х на ребрі DD₁.

          Побудову шуканого перерізу проведемо в наступному порядку: спочатку будуємо переріз призми площиною β, паралельною до площини  МNК, яка проходить через точку Х (див. задачу 1, б); потім будуємо шуканий переріз площиною,  паралельною до площини  β та той, що проходить через точку  F.  Чотирикутник     FQRТ – шуканий переріз.

План  побудови.

1. Будуємо площину МNК.  МN – слід (МNК) на ( ВСС₁), МК – слід (МNК) на (АВС),  КN – слід (МNК) на ( DСС₁).
2. Будуємо допоміжну площину β║(МNК), яка проходить через точку Х.

ХV║КN,  Х є DD₁,  ХV∩D₁С₁= V,  ХV∩СС₁= С₂,  ХV∩DС= S₁,  

S₁ S₃║МК,  S₁S₃∩ВС= S₃,  S₁С₂∩В₁С₁= Е;

З’єднуємо   точки Х та S₂, Е та V.

ХVЕS₃S₂ – допоміжний переріз.

3. Будуємо площину α₃, яка паралельна площині МNК.

FТ║ S₂Х,   FТ∩А₁D₁= Т;

ТR║МК║ЕV,   ТR∩В₁С₁=R;

RQ║МN,  RQ∩ВВ₁=Q.

З’єднуємо  Q та F.

FQRТ – шуканий переріз.

Задача  2.  Побудувати переріз піраміди SАВС площинами α₁, α₂, α₃, паралельними до площини КМN, де К є АС, М є ВС,  N є SС, які проходять через точку Р, задану наступним чином:

а) на ребрі SВ;

б) на грані SАВ;

в) на прямій SВ таким чином, що точка В лежить між точками S та Р.

 

Тим учням, які розібралися в особливостях розв’язання задач цього типу, пропонується розв’язати задачу 2, б самостійно. Паралельно проводиться робота с більш слабкими учнями. Розв’язується задача 2,а під керівництвом

вчителя.

Розв’язання

      а)  Побудуємо переріз піраміди  площиною КМN. Так як площина проходить  через точку Р, яка лежить в площині SВС, то площина α₁

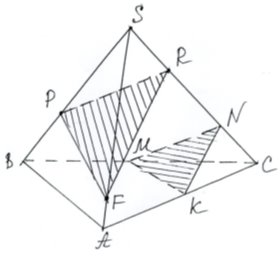                                                                   перетинає площину SВС по прямій,

                                                                   яка проходить через  точку Р. І так як

                                                                   площина α₁ паралельна до площини

                                                                   КМN, то сліди площини α₁ та

                                                                   площини КМN на площині SВС

                                                                   паралельні. Тому в площині SВС 

                                                             через точку Р проводимо пряму РR.

                                                                       Міркуючи аналогічно, проводимо в             

площині SАС через точку R  пряму RF║КN.

         З’єднаємо точку Р з точкою F. Трикутник РRF – шуканий переріз.

В зошитах записуємо план побудови.

1. Будуємо площину КМN.

МN - слід (КМN) на (SВС);    КN - слід (КМN) на (SАС);  

МК - слід (КМN) на (АВС);

2. РR║МN,     РR∩SС=R;
3. FR║КN,     FR∩SА=F;
4. З’єднаємо точку Р з точкою F.

РRF – шуканий переріз.

ІV. Підсумки уроку.

    Звертається увага на головне в розв’язуванні задач по цій темі, колективно аналізуються типові особливості задач.

V. Домашнє завдання.

    Розв’язати задачу  2, в.

Задача 2. в) На ребрах АС, ВС та СС₁ призми АВСА₁В₁С₁ Задані відповідно точки R, Q, V. Побудуйте переріз призми площиною RQV, яка проходить

через точку Р, заданій на ребрі ВВ₁.

 

Література

1. Г. П. Бевз. Геометрія: Підручник для учнів 10 – 11 класів з поглибленим вивченням математики. – К.: Освіта, 2000.
2. Я. Є. Гольберг. З чого  починається розв’язання стереометричної задачі: Посібник для вчителя. – К.: Радянська школа, 1990.
3. І. Ленчук. Метод внутрішнього проектування в метричних задачах стереометрії.//Математика в школі, -  2003, №8 – с. 19.
4. В. М. Литвиненко. Стереометрія в типових задачах: Книга для вчителя. – К. Школа – Прес, 1995, - 320 с. – (Бібліотека журналу  «Математика в школі»).
5. Л. М. Лоповок. Збірник задач з геометрії для 10 – 11 класів: Навчальний посібник. – К.: Освіта, 1993, - 160 с.
6. З. І. Слєпкань. Методика навчання математики: Підручник для студентів мат. спеціальностей пед.. навч. закладів. – К.: зодіак – ЕКО, 2000. – 520 с.
7. Активні форми організації процесу навчання (Методичні рекомендації), - Луганськ, 1998.