Урок "Паралельність прямих і площин"

Урок №20

Тема: Паралельність  прямої і площини

Мета: працювати над засвоєнням учнями теореми про влас­тивiсть паралельних прямої i площини, а також опорних вiдомостей про пряму, паралельну двом площинам, що перетинаються; сформу­вати первиннi вмiння вiдтворювати цi твердження, розв’язувати за­дачi з використанням вивчених понять; продовжувати роботу iз закрiплення знань означення та ознаки прямої, паралельної площинi, а також iз формування вмiнь викорис­товувати вивченi поняття для розв’язування задач.

Тип уроку: засвоєння знань, формування первинних умiнь.

Наочнiсть та обладнання: презентація «Паралельність прямої і площини»

Хiд уроку

І. Органiзацiйний етап

Перевiрка готовностi учнiв до уроку, налаштування на роботу.

ІІ. Перевiрка домашнього завдання

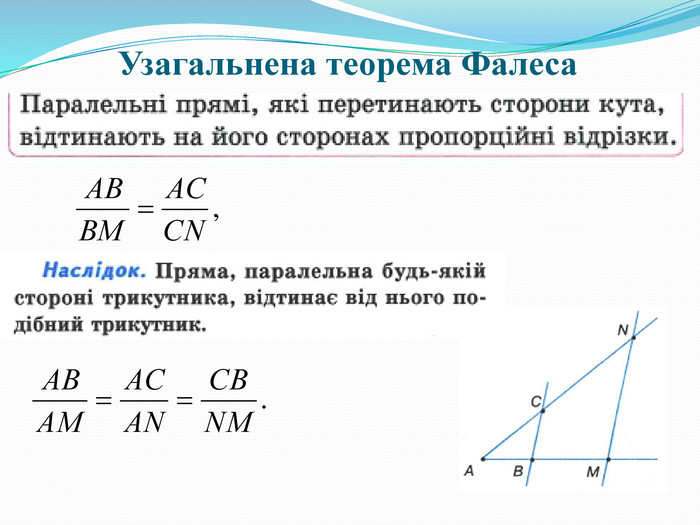
№ 3.27, № 3.31,  № 3.36. (Слайд 2-3)

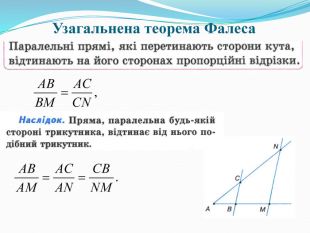
Обговорення № 3.27: (Слайд  2)

1. Чим є КМ для трикутника ОА₁В₁? Чому?
2. Назвіть середні лінії  інших трикутників?
3. Сформулюйте властивість середньої лінії трикутника.
4. Що можна сказати про трикутники KMN  та АВС?
5. Назвіть правильну відповідь до задачі.

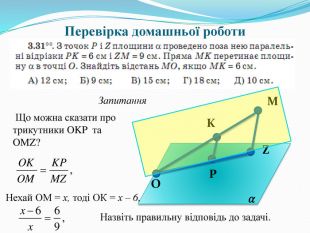
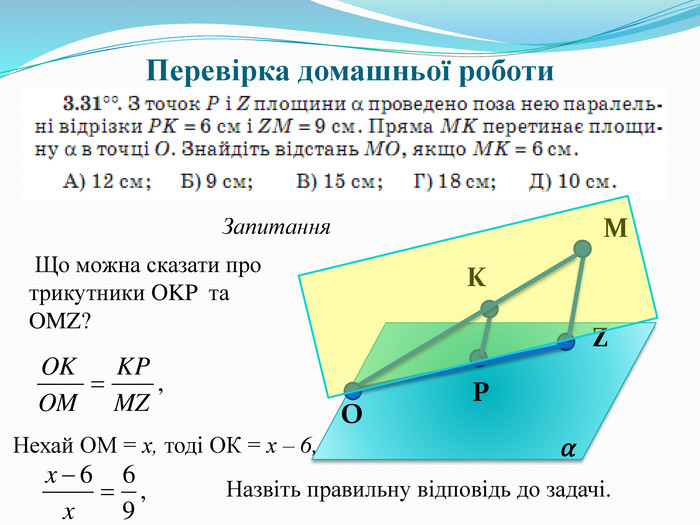
Обговорення № 3.31: (Слайд  3)

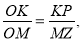1. Що можна сказати про трикутники OKP  та OMZ?
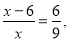2. Поясніть чому
   
    
3. Нехай ОМ = х, тоді ОК = х – 6,
   
   Назвіть правильну відповідь до задачі. ( 18 см)

Обговорення № 3.36: (Слайд  4)

1. Проведемо  площину β через прямі TP  ∥ SR .   Чи можемо це зробити?
2. TS – пряма перетину площин. Чому?
3. N ∊ TS. Чому?
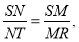4. ∆SNM ∾ ∆STR. Поясніть чому. 
5. Чи вірно складена пропорція?  
6. Нехай TN = х, тоді SN =  … (10 – x),
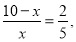7.                      Назвіть відповідь до задачі. (6см)

ІІІ. Формулювання мети й завдань уроку

За логiкою вивчення геометрiї, пiсля вивчення  взаємного розміщення прямої і площини,  означення прямої, паралельної площинi, випливає необхідність розгля­нути ознаку та  властивостi цього вiдношення. Отже, завдання на цей урок - вивчення ознак та властивостей прямої, паралельної площинi.

ІV. Актуалiзацiя опорних знань i вмінь

Фронтальна бесiда

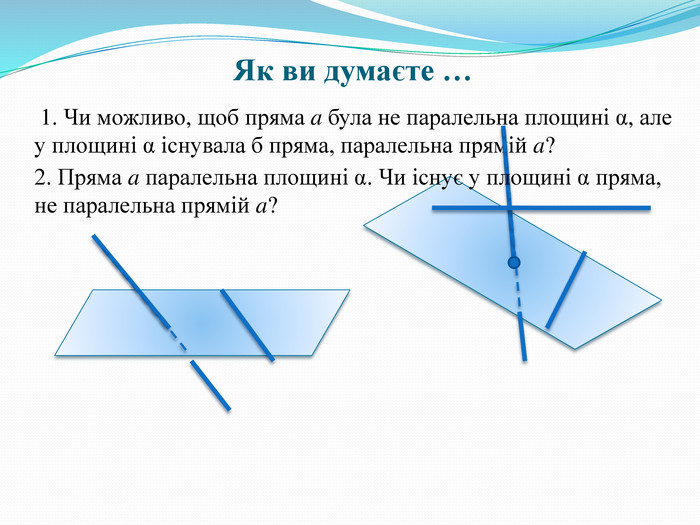
1.  Чи можливо, щоб пряма a була не паралельна площинi α, але у площинi α iснувала б пряма, паралельна прямiй a? (Слайд 5)

2.  Пряма a паралельна площинi α. Чи iснує у площинi α пряма, не паралельна прямiй a? (Слайд 5)

3. Прямi a i b паралельнi. Як можуть бути розмiщенi пряма b i площина α, якщо: (Слайд 6)
1) пряма a i площина α паралельнi;
2) пряма a i площина α перетинаються;

3) пряма a лежить у площинi α?

V. Вивчення нової теми

1. Означення прямої, паралельної площинi. Позначення.(Слайд 7).

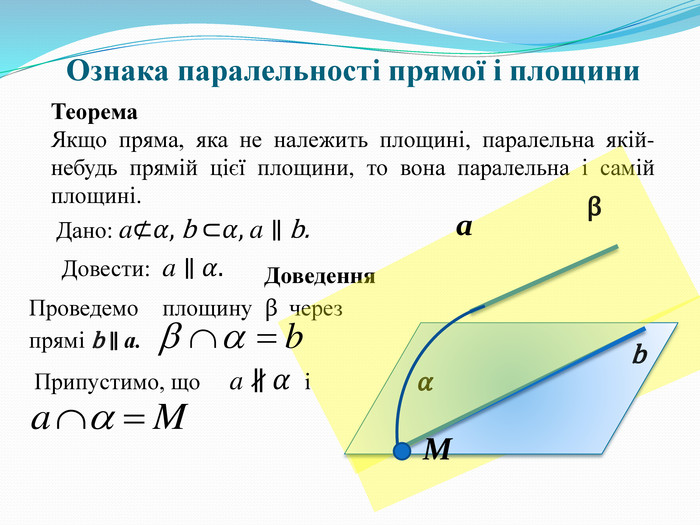
2.  Ознака паралельності   прямої  і площини (з доведенням). (Слайд 8).

3. Спосіб доведення від супротивного полягає в тому, що:

1) робимо припущення, протилежне тому, що треба довести;
2) міркуваннями доходимо до висновку, що суперечить або умові твердження, що доводиться, або одній з аксіом, або доведеній раніше теоремі, або припущенню;
3) робимо висновок – наше припущення неправильне, а тому правильним є те, що треба було довести.

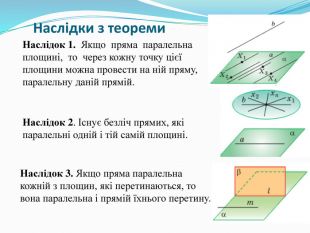
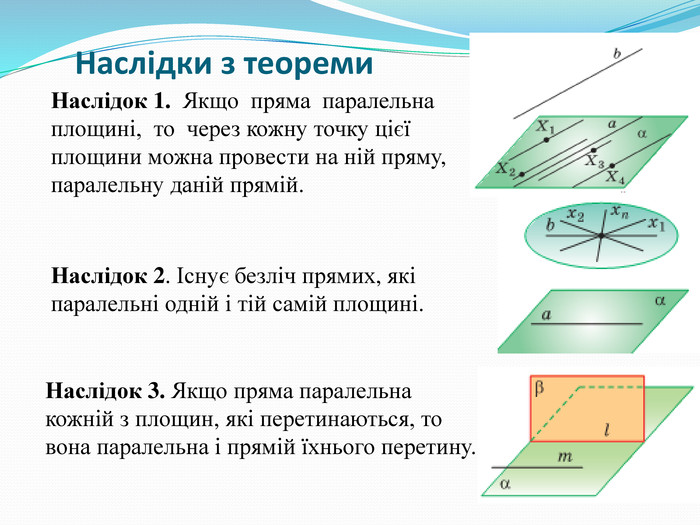
4. Наслідки з теореми. (Слайд 10).

Наслідок 1.  Якщо  пряма  паралельна  площині,  то  через кожну точку цієї площини можна провести на ній пряму, паралельну даній прямій.

Наслідок 2. Існує безліч прямих, які паралельні одній і тій самій площині.

Наслідок 3. Якщо пряма паралельна кожній з площин, які перетинаються, то вона паралельна і прямій їхнього перетину.

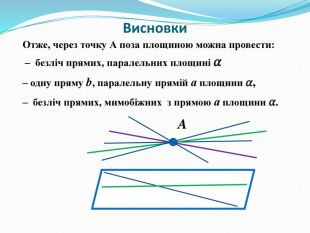
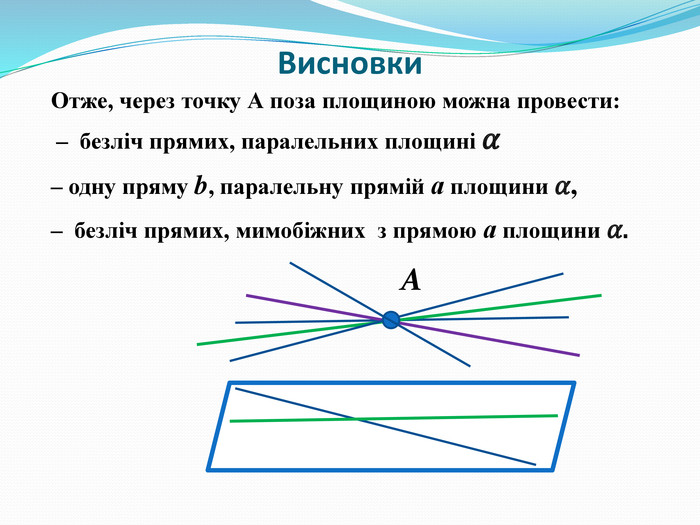
4.  Висновки (Слайд 10). Отже, через точку А поза площиною можна провести:
   –  безліч прямих, паралельних площині