Урок "Взаємне розміщення прямих у просторі"
Архів складається з повного конспекту уроку+презентація до уроку+тест. Презентація містить теоретичний матеріал до уроку. У конспекті уроку указано, в якій частині уроку використовувати той чи інший слайд. На кінець уроку доцільно учнями пройти тест, для перевірки рівня засвоєння знань. Рекомендую залучити учнів-помічників для оцінення тесту, для цього роздрукувати відповіді на листочках.
- розм прям.docx docx
- розміщення прямих у просторі.pptx pptx
- .docx docx
Конспект уроку
Тема: Взаємне розміщення двох прямих у просторі: прямі, що перетинаються, паралельні та мимобіжні прямі
Мета: повторити, узагальнити й систематизувати знання, набутi учнями пiд час вивчення планіметрії про взаємне розмiщення двох прямих на площинi, а також доповнити цi знання вiдомостями про можливi випадки взаємного розмiщення двох прямих у просторi; домогтися свiдомого засвоєння поняття про мимобiжнi прямі; домогтися засвоєння знань змiсту теорем, що виражають ознаки паралельностi прямих у просторi та мимобiжних прямих, а також схеми їх доведення.
Тип уроку: засвоєння знань, формування вмінь.
Наочнiсть та обладнання: Презентація «Взаємне розміщення прямих у просторі», тест на два варіанти
Хiд уроку
І. Органiзацiйний етап
Перевiрка готовностi учнiв до уроку, налаштування на роботу.
ІІ. Повторення вивченого матеріалу
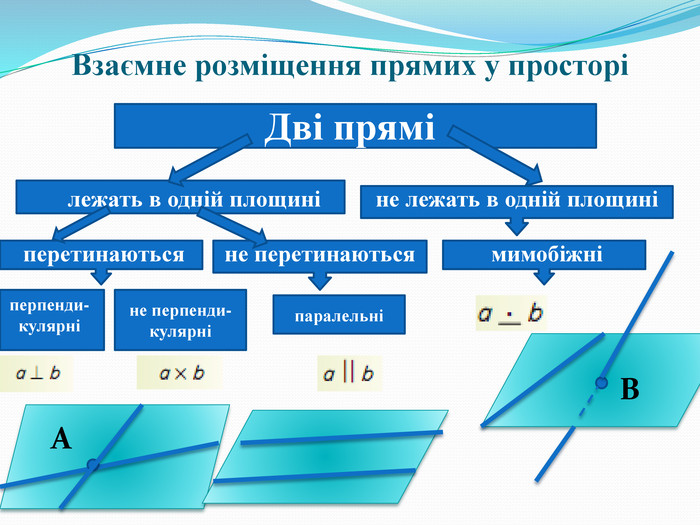
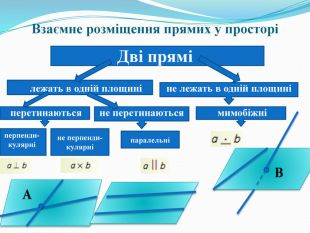
Згадайте взаємне розміщення прямих на площині, у просторі.(Слайд 2)
ІІІ. Повідомлення теми і мети уроку. Вивчення нової теми
-
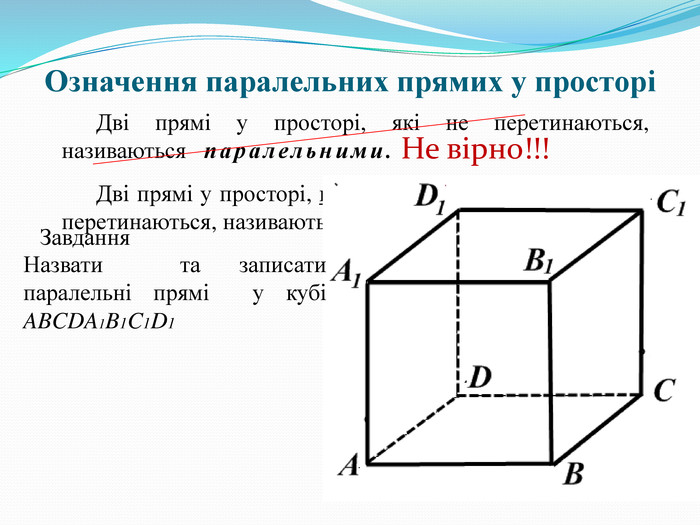
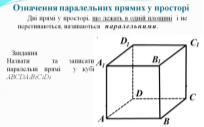 Означення паралельних прямих у просторі (Слайд 3). Завдання: назвати паралельні прямі на малюнку.
Означення паралельних прямих у просторі (Слайд 3). Завдання: назвати паралельні прямі на малюнку.
-




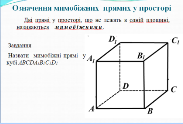
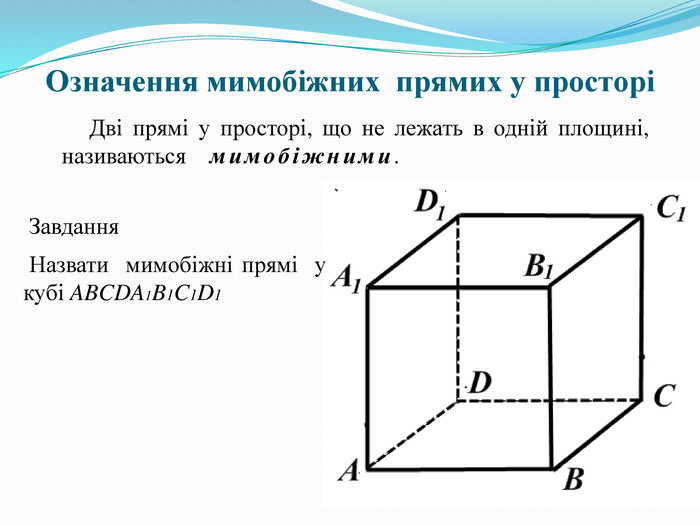
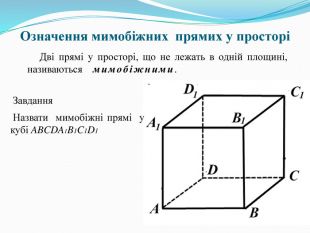
 Означення мимобіжних прямих у просторі (Слайд 4). Завдання: назвати мимобіжні прямі на малюнку.
Означення мимобіжних прямих у просторі (Слайд 4). Завдання: назвати мимобіжні прямі на малюнку.
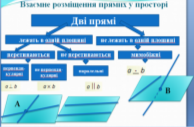
- Закінчить речення: Дві прямі, які мають спільну точку … (перетинаються). Дві прямі, які не перетинаються і лежать в одній площині … (паралельні). Дві прямі, які не перетинаються і не паралельні … (мимобіжні). Дві прямі, які мають дві спільні точки …(збігаються)(Слайд 5).
- Властивість паралельних прямих у просторі. Теорема. (Слайд 6).
-

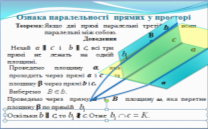

 Ознака паралельності прямих у просторі. Теорема. (Слайд 7).
Ознака паралельності прямих у просторі. Теорема. (Слайд 7).
-

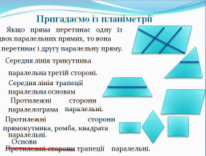
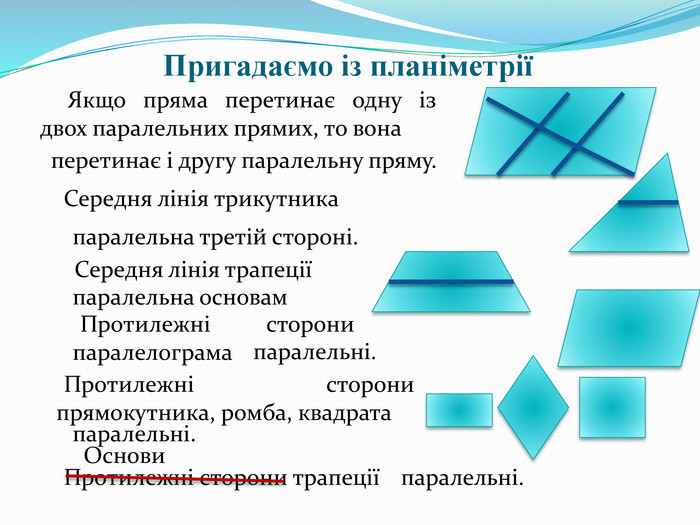
 Пригадаємо із планіметрії. (Слайд 8).
Пригадаємо із планіметрії. (Слайд 8).
- Ознака мимобіжності прямих у просторі. (Слайд 9).
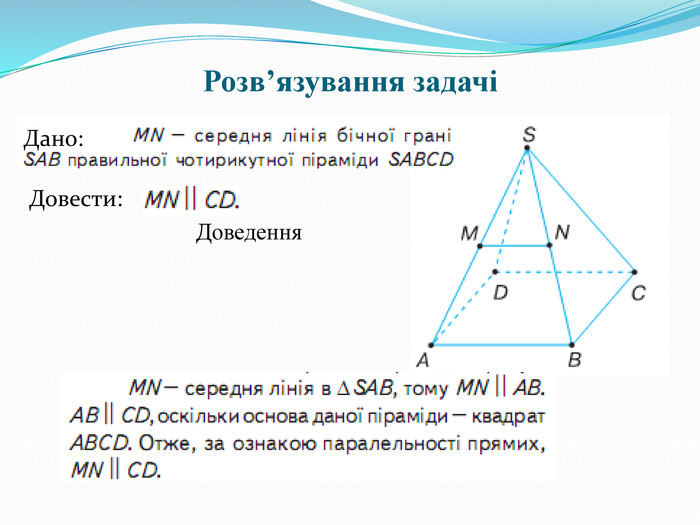
- Розв'язування задачі. (Слайд 10).
-
 Висновки.
Висновки.
Щоб встановити паралельність двох прямих, покажіть, що: або існує пряма, якій паралельна кожна з даних прямих, або відрізки даних прямих є протилежними сторонами паралелограма (чи основами трапеції, чи основою і середньою лінією трикутника тощо).
З означення паралельних прямих та доведеної теореми випливає, що через дві паралельні прямі можна провести площину, і до того ж тільки одну.
У просторі справджуються всі властивості двох паралельних прямих, які ви вивчали в планіметрії. (Слайд 11).
![]()
![]()
![]()
 IV. Закріплення вивченого матеріалу
IV. Закріплення вивченого матеріалу
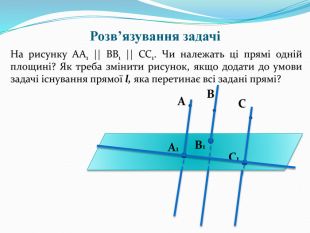
- Виконання вправи
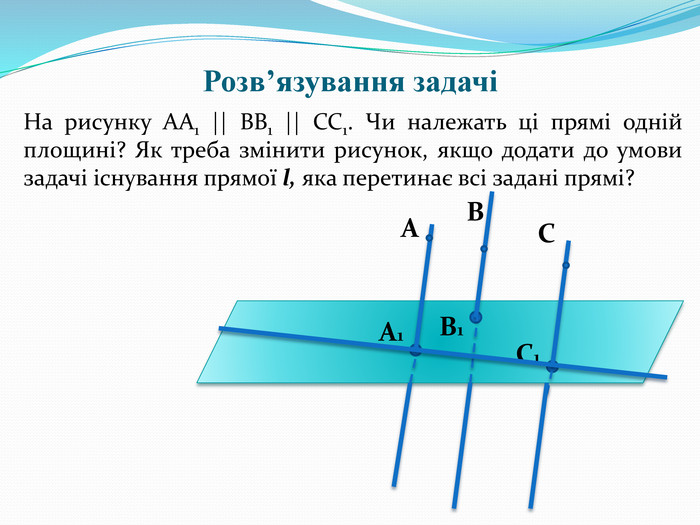
На рисунку AA1 || BB1 || CC1 .Чи належать цi прямi однiй площинi? Як треба змiнити рисунок, якщо додати до умови задачi iснування прямої l, яка перетинає всi заданi прямi? (Слайд 12)
- Тест на два варіанти.
Варіант 1
- Відомо, що прямі a і b лежать на одній площині. Укажіть неможливий варіант взаємного розміщення цих прямих.
 А) a і b перетинаються; Г) a і b не паралельні;
А) a і b перетинаються; Г) a і b не паралельні;
Б) a і b не перетинаються; Д) a і b мимобіжні.
В) a і b паралельні;
-
 Дві прямі k і l паралельні прямій х. Укажіть взаємне розміщення прямих k і l. А) Мимобіжні; Б) паралельні; В) перетинаються.
Дві прямі k і l паралельні прямій х. Укажіть взаємне розміщення прямих k і l. А) Мимобіжні; Б) паралельні; В) перетинаються.
-
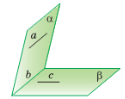
 На рисунку 1 зображено дві площини
На рисунку 1 зображено дві площини
Геометрія 10 клас
Тест (на 10 хвилин)
Тема: Взаємне розміщення двох прямих у просторі: прямі, що перетинаються, паралельні та мимобіжні прямі
Варіант 1
- Відомо, що прямі a і b лежать на одній площині. Укажіть неможливий варіант взаємного розміщення цих прямих.
 А) a і b перетинаються; Г) a і b не паралельні;
А) a і b перетинаються; Г) a і b не паралельні;
Б) a і b не перетинаються; Д) a і b мимобіжні.
В) a і b паралельні;
-
 Дві прямі k і l паралельні прямій х. Укажіть взаємне розміщення прямих k і l. А) Мимобіжні; Б) паралельні; В) перетинаються.
Дві прямі k і l паралельні прямій х. Укажіть взаємне розміщення прямих k і l. А) Мимобіжні; Б) паралельні; В) перетинаються.
-
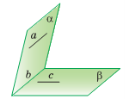
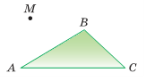 На рисунку 1 зображено дві площини
На рисунку 1 зображено дві площини


про публікацію авторської розробки
Додати розробку


















-

Klimchuk Olena
22.09.2022 в 13:23
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Авжабарова Мария
29.06.2022 в 10:28
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Горик Руслана Миколаївна
05.10.2021 в 22:22
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Катрін Альона Анатоліївна
20.09.2021 в 22:47
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Лаганович Наталія
19.09.2021 в 12:30
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Крутько Світлана Олексіївна
10.09.2021 в 05:46
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Ятел Інна Григорівна
11.11.2020 в 10:23
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Ятел Інна Григорівна
11.11.2020 в 10:23
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кулініч Лариса
30.09.2020 в 13:45
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Стефаник Алла Миколаївна
15.10.2019 в 22:48
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
-

Рогоза Ірина Федорівна
27.09.2018 в 20:49
Дякую за чудову презентацію)
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 8 відгуків