Конспект уроку. Алгебра 10 клас.
Тема уроку: Синус, косинус, тангенс і котангенс кута.
Мета уроку: Повторити означення тригонометричних функцій гострого кута прямокутного трикутника і ввести означення тригонометричної функції довільного кута.
І. Організаційний момент.
II. Повторення відомостей про тригонометричні функції гострих кутів прямокутного трикутника.


в) 2 cos 30° + 6 cos 60° – 4 tg 45°; г) 2 ctg 60° – 2 sin 60° . 6. Спростіть:
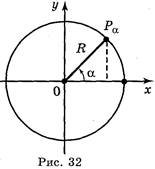 a) (l – cosα)(l + cosα); 6) tgα – ctgα + sin2 α + cos2 α. III. Повторення відомостей про тригонометричні функції довільного кута. У курсі геометрії для кутів від 0° до 180° було дано означення синуса, косинуса, тангенса за допомогою кола. Нагадаємо ці означення. Нехай дано коло радіуса R, центр якого знаходиться у початку координат. Відкладемо від додатної півосі у верхню півплощину кут α, друга сторона якого перетне коло в точці Рα(х; у) (рис. 32).
a) (l – cosα)(l + cosα); 6) tgα – ctgα + sin2 α + cos2 α. III. Повторення відомостей про тригонометричні функції довільного кута. У курсі геометрії для кутів від 0° до 180° було дано означення синуса, косинуса, тангенса за допомогою кола. Нагадаємо ці означення. Нехай дано коло радіуса R, центр якого знаходиться у початку координат. Відкладемо від додатної півосі у верхню півплощину кут α, друга сторона якого перетне коло в точці Рα(х; у) (рис. 32).
Синусом кута називається відношення ординати точки y
Рα(х; у) кола до його радіуса: sin ![]() .
.
R
Косинусом кута називається відношення абсциси точки Рα(.х; у) кола до його x
радіуса: cos ![]() . R
. R
Тангенсом кута називається відношення ординати точки Рα(х; у) до її y
абсциси:tg ![]() . x
. x
Котангенсом кута називається відношення абсциси точки Рα(х; у) до її
Роганін Алгебра 10 клас, Урок 5 2
x
 ординати: ctg
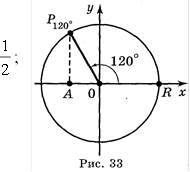
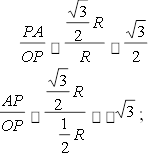
ординати: ctg ![]() . y Приклад 1. Знайти sin α, cos α, tg α, ctg α, якщо α = 120°. Побудувавши точку Р120º, маємо (рис. 33):
. y Приклад 1. Знайти sin α, cos α, tg α, ctg α, якщо α = 120°. Побудувавши точку Р120º, маємо (рис. 33):
1
- ![]() R
R
sin120o ; cos120o ![]() OA 2
OA 2
OP R
1
- R
![]() tg120o ctg120o OP 2 1 ;
tg120o ctg120o OP 2 1 ;
AP 3 3
- R
2
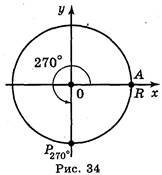 Якщо будь-який кут розглядати як фігуру, утворену обертанням променя навколо своєї початкової точки у двох можливих напрямах (додатному — проти годинникової стрілки, від'ємному — за годинниковою стрілкою), то дане визначення можна використовувати для будь-яких кутів. Приклад 2. Знайти sin α, cos α, tg α, ctg α, якщо α = 270°. При повороті на 270° навколо точки О радіус ОА, який дорівнює R, перейде в радіус ОР, тоді (рис. 34)
Якщо будь-який кут розглядати як фігуру, утворену обертанням променя навколо своєї початкової точки у двох можливих напрямах (додатному — проти годинникової стрілки, від'ємному — за годинниковою стрілкою), то дане визначення можна використовувати для будь-яких кутів. Приклад 2. Знайти sin α, cos α, tg α, ctg α, якщо α = 270°. При повороті на 270° навколо точки О радіус ОА, який дорівнює R, перейде в радіус ОР, тоді (рис. 34)
Р270º·(0; -R ) і, отже, sin 270° = ![]() R = -1, cos 270° =
R = -1, cos 270° = ![]() 0 = 0,
0 = 0,
R R
0 ctg270° = ![]() = 0 , tg 270° не має змісту.
= 0 , tg 270° не має змісту.
1
Із курсу геометрії відомо, що величина кута в градусах виражається числом від 0° до 180''. Кут Повороту може виражатися в градусах, яким завгодно дійсним числом від - до +.
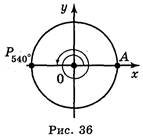
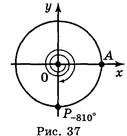
Приклад 3. Якщо початковий радіус ОА зробив повний оберт проти годинникової стрілки, то кут повороту буде дорівнювати 360° (рис. 35). Якщо початковий радіус ОА зробив півтора оберти проти годинникової стрілки, то кут повороту буде дорівнювати 540º (рис. 36). Якщо початковий радіус ОА зробив два повних оберти і чверть оберту за годинниковою стрілкою, то кут повороту буде дорівнювати 2 (-360°) - 90° = - 810° (рис. 37).
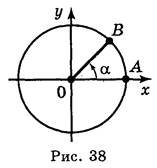 Розглянемо радіуси ОА і ОВ. Існує безліч кутів повороту, при яких початковий радіус ОА переходить у радіус ОВ (рис. 38). Нехай <AОВ = α, тоді відповідні кути повороту будуть дорівнювати α + 360°n, де n — ціле число (п Ζ).
Розглянемо радіуси ОА і ОВ. Існує безліч кутів повороту, при яких початковий радіус ОА переходить у радіус ОВ (рис. 38). Нехай <AОВ = α, тоді відповідні кути повороту будуть дорівнювати α + 360°n, де n — ціле число (п Ζ).
Якщо початковий радіус переходить у радіус ОВ при повороті на кут а, то в залежності від того, у якій четверті буде радіус 0B, кут α називають кутом цієї чверті. Так, якщо 0° < α < 90°, то α – кут І чверті; якщо 90° < α < 180°, то α — кут II чверті; якщо 180° < α < 270°, то α — кут III чверті; якщо 270° < α < 360°, то α — кут IV чверті. Кути 0°; ±90°; ±180°; ±270°; ±360° не відносяться ні до якої чверті.
У курсі геометрії було доведено, що значення синуса, косинуса і тангенса кута α, де 0° < α < 180° залежить тільки від α і не залежить від довжини R. І в загальному вигляді sin α, cos α, tg α, а також ctg α залежать тільки від кута α.
Вирази sin α і cos α, визначені для будь-яких а, так само як для будь-якого
![]() кута повороту, можна знайти відношенням y і x .
кута повороту, можна знайти відношенням y і x .
R R
Вираз tg α має смисл при будь-яких а, крім кутів повороту ±90°; ±270°; ±450°, тобто α 90°+180° n , (п Ζ).
Вираз ctg α має смисл при будь-яких а, крім кутів повороту 0°; ±180°; ±360°.., тобто, α 180° n , (п Ζ).
Кожному допустимому значенню α відповідає єдине значення sin α, cos α, tg α, ctg α, тому синус, косинус, тангенс, котангенс є функціями кута α. Їх називають тригонометричними функціями. Виконання вправ
1. Чому дорівнюють кути повороту, які показано на рисунку 39.
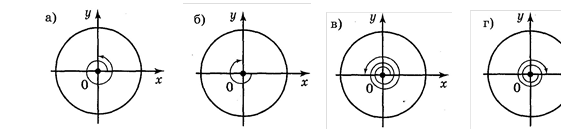
Рис. 39
2. Накресліть коло із центром у початку координат і побудуйте кут повороту, що дорівнює: а) 135°; б) -120°; в) 540°; г) -810°.
3. Запишіть всі кути поворотів, при яких радіус ОА переходить у радіус ОВ
(рис. 40).
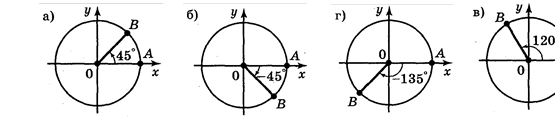
Рис. 40
4. Побудуйте коло з центром у початку координат і кути повороту, що дорівнюють:
а) 90° + 360° n, (п Z); б) 180° + 360° n, (п Z);
в) –90º + 180° n, (п Z); г) ±60° + 360º n, (п Z).
5. Визначте, кутом якої чверті є кут α, якщо кут а дорівнює:
а) 181°; б) 179°; в) 271°; г) 361°; д) 345°; є) 800°.
Роганін Алгебра 10 клас, Урок 5 4
IV. Підсумок уроку.
V. Домашнє завдання.
§ 7. Вправи № 7.4, 7.6, 7.10, 7.18.

про публікацію авторської розробки
Додати розробку
