конспект уроку алгебра 9 клас "Розв'язання лінійних нерівностей з однією зміною та їх системи"
Тема. Розв’язання лінійних нерівностей з однією змінною та їх системи.
Мета: навчальна: відтворити знання про лінійні нерівності з однією змінною та їх системи; удосконалювати вміння учнів розв’язувати нерівності з однією змінною та їх системи; формувати навички самостійної роботи;
розвивальна: розвивати увагу, пам'ять, вміння бачити закономірності, розвивати культуру математичного мовлення;
виховна: виховувати наполегливість у досягненні мети, почуття відповідальності, толерантність.
Тип уроку: формування вмінь та навичок.
Обладнання : роздавальний матеріал, мультимедійна презентація, картки контролю, картки «Лото».
Хід уроку
І. Формулювання теми, визначення мети, завдань уроку.
Слово вчителя: Ми любим все- і жар холодних чисел,
І божество у строгості рівнянь,
Але нерівності любого змісту
Торують шлях в країну знань!
Тема сьогоднішнього уроку «Розв’язання лінійних нерівностей з однією змінною та їх системи». Досягти успіху можна тоді, коли перед вами стоїть мета. Тому сформулюємо мету уроку. Сьогодні ми:
- повторимо відомості про лінійні нерівності з однією змінною та їх системи;
- розширимо, узагальнимо знання про лінійні нерівності з однією змінною та їх системами;
- повторимо алгоритм розв’язання нерівностей з однією змінною;
- вдосконалюємо навички з застосуванням алгоритму до розв’язання нерівностей з однією змінною;
- розвиватимемо увагу, пам'ять, мислення, культуру математичного мовлення.
У вас на столах є «піктограми настрою» . Покажіть який у вас зараз настрій.
Також у вас на столах є картки самоконтролю, у яких ви виставляєте одержані бали за кожний вид роботи.
|
|
Кількість правильних відповідей |
Загальна кількість балів |
|
Теоретичний матеріал (за кожну правильну відповідь 1 бал) |
|
|
|
Тестові завдання ( за кожну правильну відповідь 0,5 балів) |
|
|
|
Завдання №1 |
|
|
|
Завдання №2 |
|
|
|
Завдання №3 |
|
|
|
Математичне лото |
|
|
|
Виконання тестових завдань в зошиті ( за кожну правильну відповідь 1 бал) |
|
|
|
Всього |
|
|
Отже побажаємо один одному успіху, і пам’ятаємо , що мудрим ніхто не народився, а навчився.
ІІ. Актуалізація опорних знань
а) перевірка домашнього завдання;
б) перевірка теоретичного матеріалу (учні задають один одному питання):
1. Що називається нерівністю?
2.Що називається числовою нерівністю?
3.У якому випадку число а вважається більшим за число в?
4.Яку нерівність називають лінійною нерівністю з однією змінною?
5.Що називають розв’язком лінійної нерівності з однією змінною?
6. Що означає розв’язати нерівність?
7. Властивості числових нерівностей.
8. Які нерівності називаються рівносильними?
9.Що є системою нерівностей з однією змінною?
10. Що називається розв’язком системи лінійних нерівностей?
11.Щор означає розв’язати системи нерівностей?
в) виконання тестових завдань
|
1 |
а > в |
А |
а – в = 0 |
|
2 |
а ≥в |
Б |
а – в > 0 |
|
3 |
а = в |
В |
а – в ≤ 0 |
|
4 |
а < в |
Г |
а – в ≥ 0 |
|
|
|
Д |
а – в <0 |
1. Встановити відповідність між висловленням (1-4) та наслідком із нього (А-Д)
|
1 |
х< 5 |
А |
(0; 5] |
|
2 |
х ≥ 5 |
Б |
(-∞; 5) |
|
3 |
0 < х ≤ 5 |
В |
(-∞; -5) |
|
4 |
х< -5 |
Г |
(-5; +∞) |
|
|
|
Д |
[5; +∞) |
2. Встановити відповідність між нерівностями (1-4) та числовими проміжками (А-Д)
3.Відомо, що а > в. Яке з поданих нерівностей є неправильною?
|
А |
Б |
В |
Г |
Д |
Е |
|
3а >3 в |
а- 70 > в-70 |
а -5> в-10 |
-6а <-6 в |
а:7 > в:7 |
а+6 > в+6 |
4.Серед наведених нерівностей укажіть лінійну нерівність з однією змінною.
|
А |
Б |
В |
Г |
Д |
|
2< |
|
х2 -5 >0 |
|
х+у >8 |
5.Яка з поданих нерівностей рівносильні?
|
А |
Б |
В |
|
5х +1 >0 і 5х > 1 |
3х < 0 і х < 0 |
-2х > 0 і х > 0 |
6. Які з поданих чисел є розв’язком нерівності 3х +1 >2 ?
|
А |
Б |
В |
Г |
Д |
|
-2 |
|
0 |
-0,5 |
4 |
7. Укажіть числа, які є розв’язком системи нерівностей ![]()
|
А |
Б |
В |
Г |
|
-10; -6; 40 |
2; 4; 6 |
-10; 8; 23 |
-2; 4; 4 |
ІІІ. Узагальнення та систематизація знань.
а)Удосконалення вмінь та навичок учнів.
1.Скільки цілих від’ємних розв’язків має нерівність?
х - ![]() -
- ![]() <
< ![]()
2. При яких значеннях х визначена функція у =![]() +
+ ![]()
3.Туристи мають повернутися на базу не пізніше через 3 години. На яку відстань вони можуть відплисти за течією річки на моторному човні, якщо його власна швидкість 18 км/год, а швидкість течії 4 км/год?
(якщо учень самостійно розв’язував завдання в картку самоконтролю виставляє 3 бали)
б)«Математичне лото.» (учні об’єднуються в групи)
Розв’язати нерівність:
- 6х > 18
- -2х > 10
-
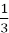 х > 9
х > 9
- – 3х + 5 ≥ 11
- х – 15 ≥ 4х +3
- 8 + 6х ≤ 13 + 6х
- 2 ( х - 1) + 4 < х +7
Картка з відповіддю
|
( 3 ; +∞) |
(27; +∞) |
(-∞; -6] |
( -∞; 5) |
( -∞; -5) |
(-∞; -2] |
х-будь-яке |
|
Г |
Р |
І |
Т |
А |
Р |
О |
Картки «Математичне лото» у клітинках знаходяться відповіді до розв’язання нерівностей. Розв’язання записують у зошитах. Знайшовши відповідь і картку, на зворотній стороні записана буква. Букви розташовуються в такому порядку, як записані нерівності. Розв’язавши усі нерівності учні одержують ім’я відомого вченого, який вперше використав знаки нерівності.( Томас Гарріот)
в)Історична довідка
Знаки нерівності (строгі знаки) <; > з’явилися вперше 1631 року в роботі англійського вченого Томаса Гарріоті. До цього писали словами « більше», «менше». Символи ≥; ≤ (нестрогі знаки) запропонував Валліс у 1670 році. Спочатку риска була вище за знак порівняння, а не під ним, як зараз. Широке розповсюдження ці знаки отримали після підтримки французьким математиком П’єром Бузі у 1734 році. У якого вони набули сучасного вигляду.
1557 році знак нерівності запропонував Роберт Рекорд. Зображення символу було набагато довше, ніж зараз. Автор пояснював, що не має в світі нічого більш рівного, чим два паралельні відрізки рівної довжини. Деякий час поширенню символу Рекорда заважала та обставина, що з античних часів такий символ використовувала для позначення паралельності прямих; у решті було вирішено символ паралельності зробити вертикальними. У Європі знак рівності ввів Лейбніц.
г) Виконання тестових завдань із взаємоперевіркою в парах(за кожне правильно виконане завдання учень отримує 1 бал)
1.Виберіть правильну числову нерівність
|
А |
Б |
В |
Г |
|
0,2>2 |
-1 < -2 |
5 ≥ |
2,36 ≤ 1,1589 |
2.Сумою нерівностей 5 > 3 і 2 > -1 є нерівність
|
А |
Б |
В |
Г |
|
4 > 5 |
4 < 5 |
7 > 2 |
7 ≥ 2 |
3.Вказати строгу нерівність
|
А |
Б |
В |
Г |
|
15 ≥ 5 |
2 ≥ 2 |
7 > -3 |
-10 ≤ -10 |
4. Яке з поданих чисел задовольняє нерівність х2 + 2х +1 ≤ 0 ?
|
А |
Б |
В |
Г |
|
-1 |
0 |
1 |
2 |
5. Скільки цілих чисел задовольняє нерівності -1 ≤ х≤ 1
|
А |
Б |
В |
Г |
|
одне |
два |
три |
чотири |
6. Знайти найменший цілий розв’язок системи нерівностей ![]()
|
А |
Б |
В |
Г |
|
-4 |
-3 |
2 |
1 |
7Знайти область визначення функції у = ![]() +
+![]()
|
А |
Б |
В |
Г |
|
(-∞; 0) |
[0; +∞) |
(0; +∞) |
(-∞;0)U(0; +∞) |
ІV.Підсумок уроку
Підрахуйте кількість балів у картки самоаналізу. Якщо кількість балів належить проміжку [27; 25], то ви отримали 10 балів. Якщо сума ваших балів потрапило до проміжку [24; 19), то ваша оцінка 9. А якщо сума балів належіть проміжку (18; 5), то ви заробили оцінку 8. Якщо ви набрали меншу кількість балів, то вам треба ще попрацювати над цією темою.
Підніміть «піктограму настрію», яка відповідає зараз вашому настрію.
І я хочу закінчити урок народною мудрістю: «Що нині втече , то завтра не зловиш».
V. Домашнє завдання
1. Знайти найменший цілий розв’язок в) 5х≥ 40, б) -7х < 15
2. Розв’язати нерівність ![]() -
- ![]() > -2
> -2
3.Знайти найбільший цілий розв’язок (х + 4)(х - 4) – 5х> (х - 1)2 -17
4. Знайти область визначення функції у = ![]() +
+![]()
5. Турист проплив на човні деяку відстань за течією річки, а потім повернувся назад, витративши на весь шлях не більше 5 годин. Швидкість човна 5 км/год. Швидкість течії 1 км/год. Яку найбільшу відстань міг проплити турист за течією річки?


про публікацію авторської розробки
Додати розробку
