Конспект уроку "Числові функції. Способи задання числових функції"

УРОК 3

Тема уроку: Числові функції. Способи задання числових функцій 

Мета: навчальна: узагальнення і систематизація знань учнів про чис­лові функції (область визначення і область значення функцій, зростаючі і спадні функції, парні і непарні функції).;

виховна: виховувати розуміння ролі математики в житті, розуміння важливості математичних знань.

Тип уроку: застосування знань та вмінь.

Хід уроку

     I.Організаційний етап

Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.

    II. Перевірка домашнього завдання

Перевірити наявність виконаного домашнього завдання та відповісти на запитання, які виникли в учнів під час його виконання.

    IІІ. Актуалізація опорних знань та вмінь учнів

  1.Як позначають порожню множину, множини натуральних, цілих, раціональних, дійсних чисел?

  2. Дайте означення рівності множин. Наведіть приклади двох рівних множин.

  3. Дайте означення перерізу, об’єднання, різниці двох множин. Наве- діть приклади. Проілюструйте за допомогою кругів Ейлера—Венна.

   4.Нехай А, В, С — деякі множини. Доведіть указані рівності та про- ілюструйте їх за допомогою кругів Ейлера—Венна: 1) (А И В) È С = А И (В И С) — сполучний закон для об’єднання; 2) (А З В) Ç С = А З (В З С) — сполучний закон для перерізу;

IV. Вивчення нового матеріалу

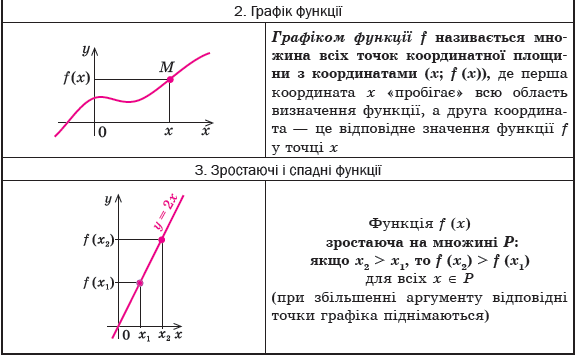
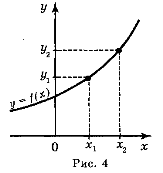Поняття функції. З поняттям функції ви ознайомилися в курсі ал- гебри. Нагадаємо, що залежність змінної y від змінної x називається функцією, якщо кожному значенню x відповідає єдине значення y. У курсі алгебри і початків аналізу ми будемо користуватися таким означенням числової функції. Числовою функцією з областю визначення D називається залеж- ність, при якій кожному числу x із множини D ставиться у відповідність єдине число y. Функції позначають латинськими (інколи грецькими) буквами. Розглянемо довільну функцію f. Число y, яке відповідає числу x (на ри- сунку до пункту 1 табл. 3 це показано стрілкою), називають значенням функції f у точці x і позначають f (x).

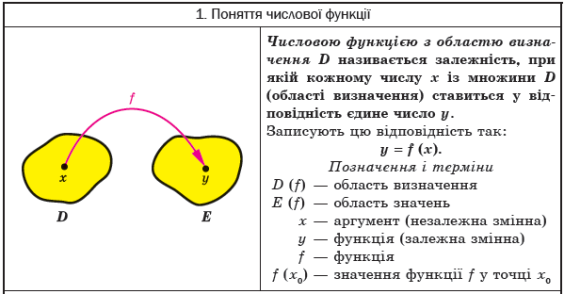
Функція у = f(x) називається зростаючою (рис. 4), якщо більшому значенню аргументу відповідає більше значення функції, тобто для будь-яких значень х₁ і х₂ з області визначення функції таких, що х₁ < х₂, виконується нерівність f(x₁) < f(x₂) і навпаки: із того, що f(x₁) < f(x₂) виконується нерівність х₁ < х₂.

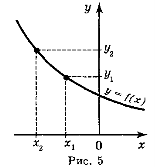Функція у = f(x) називається спадною (рис. 5), якщо більшому значенню аргументу відповідає менше значення функції, тобто для будь-яких значень х₁ і х₂ з області визначення функції та­ких, що х₁ < х₂, виконується нерівність f(x₁) > f(x₂) і навпаки: якщо у = f(x) — спадна, то із того, що f(x₁) > f(x₂), виконується нерівність х₁ < х₂.

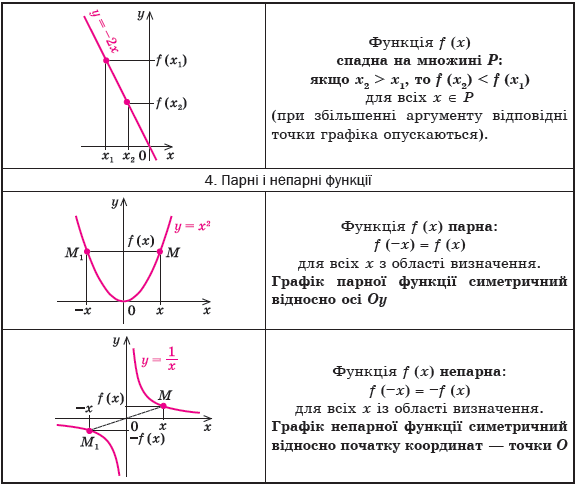
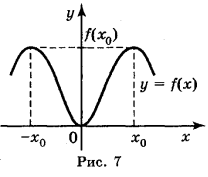Функція у = f(x) називається парною, якщо для будь-якого значення х із D(y) значення – х також належить D(y) і виконується рівність f(-x) = f(x).

Графік парної функції симетричний відносно осі ОУ (рис. 7).

Приклад 1. Чи парна функція f(x) = χ⁴ + χ² ?

Оскільки D(f) = R і f(-x) = (-х)⁴ + (-x)² = х⁴ + х² = f(x) , функція парна.

Приклад 2. Чи парна функція f(x) = х² + х ?

Оскільки D(f) = R, але f(-x) = (-х)² + (-х) = х² – х f(x), то функція не є парною.

Функція у = f(x) називається непарною, якщо для будь-якого значення х із D(y) значення -х D(y) і виконується рівність f(-x) = -f(х).

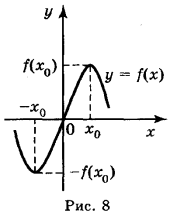
Графік непарної функції симет­ричний відносно початку координат (рис. 8).

Приклад 3. Чи непарна функція f(х) = x³ - x⁵?

Оскільки D(f) = R і f(-х) = (-х)³ - (-х) =  -х³ + х⁵ =

= -(х³ - х⁵) = -f(х), функція непарна.

Приклад 4. Чи непарна функція f(х) = х³ – х² ?

Оскільки D(f) = R і f(-x) = (-х)³ - (-х)² = -х³ - х² = -(х³ + х²)f(x) = -х³ + х², функція не є непарною.

IV. Розв’язування вправ

Ст____Впр_______________

1. Знайдіть значення функції:

 a) f(x) = у точках 1; -1; 5;б) f(x) = у точках 3; 12; 52.

Відповідь: а) f(1) = 2, f(-1) = 0; f(5) = 1,2;

б) f(3) = 0; f(12) = 3; f(52) = 7

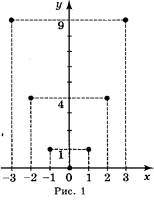
2. Функцію задано формулою у = x² на області визначення D = {-3; -2; -1; 0; 1; 2; 3}. Задайте її за до­помогою:   а)таблиці;        б)графіка.                      Відповідь: Б) рис. 1

3. Знайдіть область значень функції: а) у =  ;      б) у = -1.

Відповідь: а) Е(у) = [2; +);     б) Е(у) = [1; +).

V. Підведення підсумків уроку 

1. Знайдіть область визначення функції:

а) у = х² + х³; б) ; в) ; д) ; є) .

VI. Домашнє завдання

Ст____Впр______________