Презентація "Дослідження функції на монотонність, екстремуми функції"

Знаходження інтервалів монотонності функцій та екстремумів функції

Знаходження інтервалів монотонності функцій. Знайти область визначення функції. Дослідити функцію на парність. Дослідити функцію на періодичність. Знайти похідну даної функціїЗнайти критичні точки функції, т.б. точки, у яких її похідна у′(х)=0 дорівнює нулю або не існує. Ці точки розіб’ють область визначення на інтервали, у яких похідна зберігає знак. Визначити знак похідної у кожному з одержаних інтервалів. Для цього досить обчислити(хоча б визначити знак) значення похідної у одній з внутрішніх точок кожного інтервала. У інтервалах, де похідна додатна -функція зростає, у інтервалах, де похідна від’ємна - функція спадає. Приклад 1. Знайдіть проміжки зростання і спадання функції: у=х3−18х. Розв’язання.2.у(-х)=(−х)3−18−х=−х3+ 18х=-(х3−18х )=-у(х). Отже, функція непарна. 3. Функція неперіодична.   Знаходимо критичні точки: 3х2−18=0; 3(х2−6)=0. Звідси, х=± 6  . 1. Область визначення функції :(х3−18х )- многочлен. D(у) =R, (−∞;∞).  5. Визначаємо знак похідної. у′(-5)=3*25-18 =+у′(0)=3*0-18=-, у′(5)=+4. Знаходимо похідну функції: у′=(х3−18х)′=3х2-18. 6. Отже, похідна додатна на інтервалах ( −∞;-6) і (6; ∞), у=х3−18х – зростає на цих інтервалах. Похідна від’ємна на інтервалі (-6; 6),функція спадна на цьому інтервалі +-+х-6 6 

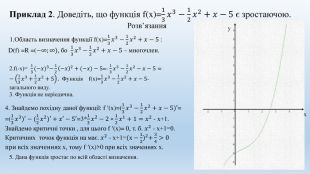
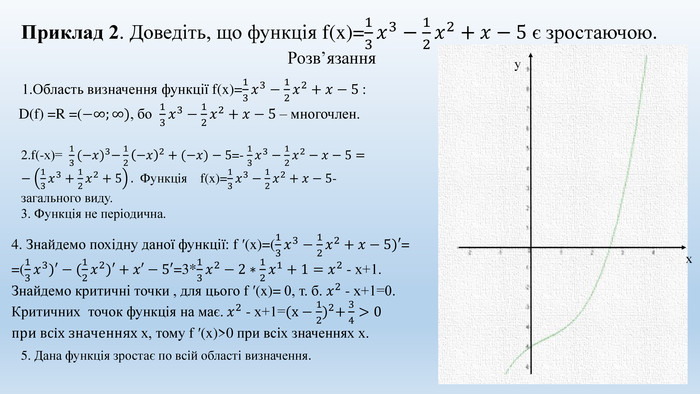
Приклад 2. Доведіть, що функція f(x)=13𝑥3−12𝑥2+𝑥−5 є зростаючою. Розв’язання 1. Область визначення функції f(x)=13𝑥3−12𝑥2+𝑥−5 : D(f) =R =(−∞;∞), бо 13𝑥3−12𝑥2+𝑥−5 – многочлен.  2.f(-х)= 13(−𝑥)3−12−𝑥2+(−𝑥)−5=- 13𝑥3−12𝑥2−𝑥−5=−13𝑥3+12𝑥2+5. Функція f(x)=13𝑥3−12𝑥2+𝑥−5-загального виду. 3. Функція не періодична.  4. Знайдемо похідну даної функції: f ′(x)=(13𝑥3−12𝑥2+𝑥−5)′==(13𝑥3)′−(12𝑥2)′+𝑥′−5′=3*13𝑥2−2∗12𝑥1+1=𝑥2 - х+1. Знайдемо критичні точки , для цього f ′(x)= 0, т. б. 𝑥2 - х+1=0. Критичних точок функція на має. 𝑥2 - х+1=(х−12)2+34>0 при всіх значеннях х, тому f ′(x)>0 при всіх значеннях х. 5. Дана функція зростає по всій області визначення.ху

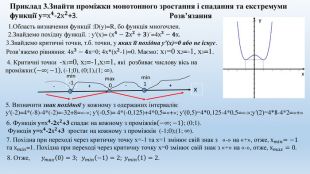
Приклад 3. Знайдіть проміжки монотонності функції f(x)=𝑥2−9𝑥+2. Розв’язання1. Область визначення функції: f(x)=𝑥2−3𝑥+2.  х+2≠0, х ≠-2, х=-2 – вертикальна асимптота. D(f)=(-∞;−2)∪(-2; ∞). 1) Знайдемо нулі функції:f(x)= 0, 𝑥2−3𝑥+2=0, 𝑥2−3=0, х=±3. Отже, нулями функції є (-3;0) та (-3;0).  х-22. f(-x)= (−𝑥)2−3(−𝑥)+2= 𝑥2−3−𝑥+2=−𝑥2−3𝑥−2 - функція загального виду, ні парна, ні непарна. Неперіодична. 3. Знайдемо похідну даної функції: f′(x)=(𝑥2−3𝑥+2)′=(𝑥2−3)′∗(х+2)−(𝑥2−3)(х+2)′(х+2)2=2х∗х+2−(𝑥2−3)(х+2)2=2𝑥2+4х−𝑥2+3(х+2)2=𝑥2+4х+3(х+2)2. Знайдемо критичні точки , для цього f ′(x)= 0, т. б. 𝑥2+4х+3(х+2)2=0, 𝑥2+4х+3=0, х1=-3, х2=-1, х ≠-2. + - - + х-3-2-14. Визначаємо знак похідної методом інтервалів: (-∞;−3), f′(−4)=+; -3ϵ (-∞;−2), то функція – зростає на (-∞;−3]; (-3;-2), f′(-2,5)=-; -3ϵ (-∞;−2), то функція – спадає на [-3;-2);(-2;-1), f′(-1,5)=- ; -1ϵ(-2; ∞), то функція – спадає на (-2;-1]; (-1; ∞), f′(2)= + ; -1ϵ(-2; ∞), то функція – зростає на [-1;+ ∞). xy5. Відповідь: функція зростає на (-∞;−3] і [-1;+ ∞) та функція спадає на [-3;-2) і (-2;-1]. 

Приклад 1. Знайти проміжки монотонного зростання і спадання та екстремуми функції у=х𝟒−𝟒х+𝟓. Знайти область визначення функції. Знайти похідну даної функціїЗнайти критичні точки функції, т.б. точки, у яких її похідна у′(х)=0 дорівнює нулю або не існує. Ці точки розіб’ють область визначення на інтервали, у яких похідна зберігає знак. Визначити знак похідної у кожному з одержаних інтервалів. Для цього досить обчислити(хоча б визначити знак) значення похідної у одній з внутрішніх точок кожного інтервала.6. У інтервалах, де похідна додатна -функція зростає, у інтервалах, де похідна від’ємна - функція спадає 7. Зліва направо похідна змінює знак з “+” на “-”, функція має максимум, зліва на право похідна змінює знак з “-” на “+”, функція має мінімум. Якщо при переході через критичну точку похідна не змінює знак, то у цій точці функція не має екстремуму.8. Обчислити екстремальні значення функції, це значить знайти значення функції у критичних точках, де вона має екстремум. 1. Область визначення функції: D(y)=R, бо х𝟒−𝟒х+𝟓-многочлен.  2. Знаходимо похідну даної функції: у′(х)=(х4−4х+5)′=4х𝟑−4. 3. Знайдемо критичні точки,т.б. точки, у яких її похідна у′(х)=0 або не існує. 4х𝟑−4=0; 4(х𝟑−1)=0; (х-1)(х2+х+1)=0; маємо х-1=0; х=1; х2+х+1)≠0 для всіх значень х з області визначення 4. Критична точка є х=1, яка розбиває числову вісь на два проміжки: −∞;1  та (1; ∞) 5. Визначити знак похідної у кожному з одержаних інтервалів.у′(0)=-4<0,  бо 0ϵ−∞;1. Функція у=х4−4х+5 –спадає на проміжку −∞;1;у′(2)=4*8-4=28>0, бо 2 ϵ(1; ∞)Функція у=х4−4х+5 –зростає на проміжку (1; ∞). х1-+6. При переході через критичну точку х=1, похідна змінює свій знак з «-» на «+». Отже, функція і цій точці досягає мінімуму.у𝑚𝑖𝑛1=14−4∗1+5=1-4+5=2. 

Приклад 2. Знайти проміжки монотонного зростання і спадання та екстремуми функції у=х3х2+4 1. Область визначення функції: D(y)=R, бо х2+4≠0 при всіх значеннях х.  2. Знаходимо похідну даної функції: у′(х)=(х3х2+4)′=(х3)′∗х2+4−х3∗(х2+4)′(х2+4)2=3х2∗х2+4−х3∗2х(х2+4)2=3х4+12х2−2х4(х2+4)2=       =х4+12х2(х2+4)2. 3. Знайдемо критичні точки, т.б. точки, у яких її похідна у′(х)=0 або не існує. х4+12х2(х2+4)2=0; х4+12х2=0, а х2+4≠0; х2* (х2+12)=0. Маємо : х=0 – єдина критична точка, х2+12 ≠0. 4. Критична точка є х=0, яка розбиває числову вісь на два проміжки: −∞;0  та (0; ∞) х05. Визначити знак похідної у кожному з одержаних інтервалів. у′(-1)=13>0,  бо (-1)ϵ−∞;0. Функція у=х3х2+4–зростає на проміжку −∞;0; у′(2)=16+48=64>0, бо 2 ϵ(2; ∞). Отже, функція у=х3х2+4 -зростає на проміжку (0; ∞). 6. Функція точок екстремуму немає.ух++

xy. Приклад 3. Знайти проміжки монотонного зростання і спадання та екстремуми функції у=х𝟒-2х𝟐+3. Розв’язання1. Область визначення функції : D(y)=R, бо функція многочлен.2. Знайдемо похідну функції. : у′(х)= (х𝟒−𝟐х𝟐+𝟑)´=4х𝟑−𝟒х.   3. Знайдемо критичні точки, т.б. точки, у яких її похідна у′(х)=0 або не існує. Розв’яжемо рівняння: 4х𝟑−𝟒х=0; 4х*(х𝟐-1)=0. Маємо: х1=0 х2=-1, х3=1.  4. Критичні точки -х1=0, х2=-1,х3=1, які розбиває числову вісь на проміжки:−∞;−1, (-1;0), (0;1),(1; ∞). 1х0-15. Визначити знак похідної у кожному з одержаних інтервалів: у′(-2)=4*(-8)-4*(-2)=-32+8=«-»; у′(-0,5)= 4*(-0,125)+4*0,5=«+»; у′(0,5)=4*0,125-4*0,5=«-»;у′(2)=4*8-4*2=«+»-+-+minmaxmin6. Функція у=х𝟒-2х𝟐+3 спадає на кожному з проміжків−∞;−1; (0;1). Функція у=х𝟒-2х𝟐+3 зростає на кожному з проміжків (-1;0);(1; ∞).  7. Похідна при переході через критичну точку х=-1 та х=1 змінює свій знак з «-» на «+», отже, х𝑚𝑖𝑛=−1 та х𝑚𝑖𝑛=1. Похідна при переході через критичну точку х=0 змінює свій знак з «+» на «-», отже, х𝑚𝑎𝑥=0. 8. Отже, 𝑦𝑚𝑎𝑥0=3;  𝑦𝑚𝑖𝑛−1=2; 𝑦𝑚𝑖𝑛1=2. 

Індивідуальні ззавдання (Для самостійної роботи, для домашньої роботи) . 1234567123456788