Розробка уроку " Похідна та її застосування до розв"язування задач.Урок-подорож країною Диференціального Числення. "
ПОХІДНА ТА ЇЇ ЗАСТОСУВАННЯ ДО РОЗВ’ЯЗУВАННЯ ЗАДАЧ.
Урок-подорож країною Диференціального Числення.
Ігри – «гімнастика розуму», тренування з комунікабельності – допомагають згуртувати колектив, сформувати організаторські навички, виховувати ініціативність, самостійність.
Для проведення уроку-подорожі клас об’єднується в чотири-п’ять команд (екіпажів). Команди знають, що вичерпна відповідь без помилок – це бали команді, тому під час підготовки сильніші учні тренують слабших, щоб забезпечити бали своїй команді, бо розуміють, що від результату роботи кожного учасника залежить успіх усієї команди. Відбувається активне спілкування членів команди, без участі вчителя, формуються навички самостійної та пошукової роботи.
Результатом уроку буде залік з теми «Застосування похідної».
Загальні правила гри.
- За командою «Консультація» учні допомагають один одному розібратися в питаннях, запропонованих учителем.
- Якщо більшість учнів не розуміють розв’язання, консультацію дає вчитель.
- Учень відповів правильно (+1) бал.
- Учень відповів неправильно (−1) бал.
- Учню підказали (−5) балів.
- Учня висміяли за неправильну відповідь або полаяли (−2) бали.
- Порушення дисципліни (−1) бал.
- Учень відповідає, всі повинні опустити руки й уважно слухати. Порушення (−1) бал.
Мета:
- закріплення та поглиблення знань учнів про похідну та її застосування до дослідження властивостей функції;
- формування вмінь застосовувати знання та способи дій у змінених і нових навчальних ситуаціях;
- розвиток підсвідомої активності учнів, формування навчально-пізнавальних дій у роботі з довідковою літературою;
- поглиблення знань учнів про моделювання процесів дійсності за допомогою апарата похідної;
- формування вміння рецензувати відповіді товаришів та коректування власних відповідей;
- формування вмінь організації та проведення дискусії з питань, що обговорюються.
Тип уроку: застосування знань, умінь навичок.
Питання, що пропонуються до обговорення на уроці:
- Виникнення поняття похідної.
- Дослідження функції.
- Моделювання процесів дійсності за допомогою похідної.
… Сила і загальність методу диференціального та інтегрального числень такі, що, не ознайомившись з ними, не можна як слід зрозуміти значення математики для природознавства та техніки і навіть повністю оцінити всю красу і принадність самої математичної науки.
ХІД УРОКУ
Перший етап уроку.
1. Вступне слово вчителя про роль поняття «похідна» в науці та техніці.
До відкриття похідної прийшли в кінці XVII ст.. незалежно один від одного два відомі вчені – Ісаак Ньютон і Готфрід-Вільгельм Лейбніц: перший, розв’язуючи задачу механіки про миттєву швидкість, а другий – геометричну задачу про проведення дотичної до кривої в певній точці.
Виникнувши з практики, поняття похідної отримало узагальнювальний абстрактний зміст, що збільшило її прикладне значення. Створення диференціального числення розширило можливості застосування математичних методів у природознавстві та техніці.
2. Організація класу
Учень повідомляє, що в подорож країною Диференціального Числення вирушають чотири команди.
Склад команди: капітан, штурман та члени екіпажу.
Учитель дає настановку: якщо в команди виникають труднощі під час виконання завдань, то вона «сигналізує» прапорцем червоного кольору, а якщо завдання виконується, то – зеленим прапорцем.
До дошки запрошуються капітани (штурмани) команд.
Мета роботи: перевірити, чи готові кораблі до подорожі. Капітанам пропонуються завдання.
Капітану 1
- Геометричний зміст похідної.
- Установити відповідність між функціями та їхніми похідними. Відповідь обґрунтувати.
|
Функція |
Похідна функція |
|
1.
2.
3.
4.
5. |
1.
2.
3.
4.
5. |
-
Знайти інтервали монотонності функції
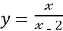 .
.
-
Знайти найбільше та найменше значення функції
 .
.
Капітану 2
- Сформулювати необхідну умову існування екстремуму функції.
- Заповнити таблицю
|
Функція |
Похідна функція |
|
1.
2.
3.
4. |
1.
2.
3.
4. |
-
Знайти проміжки на яких функція
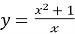 зростає.
зростає.
-
Дослідити функцію
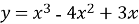 та побудувати її графік.
та побудувати її графік.
Капітану 3
- Знайти область визначення функції:
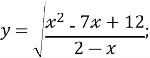
- Знайти критичні точки функції:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
Які з цих точок є точками екстремуму?
- Навести приклад функції, найбільше значення якої на деякому проміжку [а;b] не є максимумом.
- Назвати за наступними даними проміжки монотонності та точки екстремуму функції.
|
f '(x) |
+ |
− |
+ |
− |
x |
|
f (x) |
|
0 |
4 |
8 |
|
Капітану 4
- Що називається найбільшим і найменшим значенням неперервної функції, заданої на замкненому відрізку?
- Перевірити правильність заповнення таблиці. Дати обґрунтовану відповідь.
|
f (x) |
|
|
|
|
|
f '(x) |
|
|
|
|
-
Дослідити на екстремуми функцію
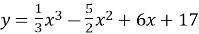 .
.
-
Показати, що функція
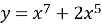 зростає на всій числовій прямій.
зростає на всій числовій прямій.
3. Поки капітани виконують завдання, вчитель проводить з іншими учнями класу (членами екіпажів) фронтальне опитування.
Питання до учнів
- Сформулюйте ознаки зростання (спадання) функції на проміжку.
- Які з поданих функцій зростають, а які спадають на всій числовій прямій?
-
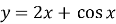 ;
;
-
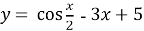 ;
;
-
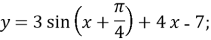
-
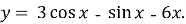
- На рисунку зображено графік диференційованої функції y=h(x). Визначте знак похідної функції на проміжках:
а) (−5;−2); б) (−2;3); в) (3;5).
Відповідь поясніть.
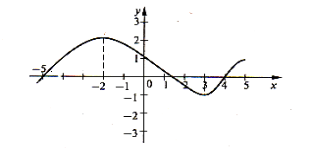
- При яких значеннях змінної функції, графіки похідних яких зображено на рисунку, мають точки максимуму та мінімуму? Назвіть ці точки.
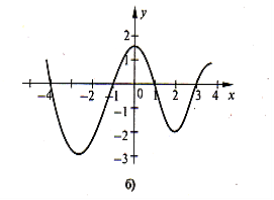
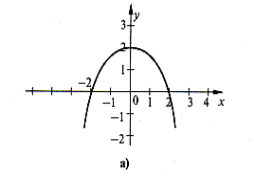
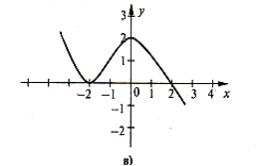
- Дослідіть функцію на екстремум:
а) ![]() =
=![]() ; б)
; б) ![]() =
=![]() ;
;
в) ![]() =
=![]() ; г)
; г) ![]() =
=![]() .
.
- Поясніть, чому наведені нижче функції не мають точок екстремуму:
а) ![]() ; б)
; б) ![]() в)
в) ![]() ; г)
; г) ![]() .
.
-
Сформулюйте алгоритм знаходження найбільшого та найменшого значень функції
 f (x) на відрізку [а;b].
f (x) на відрізку [а;b].
- На відрізку [m;n] максимум функції дорівнює 4, мінімуми функції дорівнюють 2 і −1. Яких умов не вистачає для того, щоб визначити найбільше та найменше значення функції на [m;n]?
- Чи може значення функції в точці максимуму (мінімуму) бути менше (більше) від її значення в точці мінімуму (максимуму)?
- Чи правильне твердження «…добуток двох зростаючих функцій є зростаючою функцією»?
-
Чи буде функція
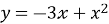 неперервною на інтервалі (1;3)?
неперервною на інтервалі (1;3)?
-
Дослідіть функцію
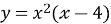 та побудуйте її графік.
та побудуйте її графік.
Другий етап уроку
1. Капітани команд беруть зі столу вчителя конверти під назвою «Важке питання». У кожному конверті декілька завдань, причому завдання між членами екіпажу розподіляють капітан і штурман.
2. Виконання учнями завдань.
Картка «Важке запитання» (зразок)
-
Знайдіть похідну функції f (x)=
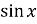 +2
+2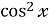 у точці
у точці 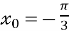 .
.
- Знайдіть область визначення функції
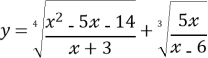
-
Знайдіть проміжки зростання та спадання функції
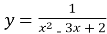
- Знайдіть критичні точки функції
![]() .
.
-
Дослідіть функцію
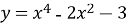 .
.
3. Захист розв’язань завдань кожним з екіпажів.
Для захисту розв’язань задач до дошки запрошуються по два учні від екіпажу: один представляє розв’язання найбільш складних задач, а інший розкриває «проспекти» розв’язання інших задач, картки з повним виділенням тих математичних знань, які довелось застосувати під час розв’язування.
4. Учитель коригує дії учнів; звертає особливу увагу на правильність і грамотність побудови графіків функцій.
Третій етап уроку
1. Капітани (штурмани) команд отримують пакети із завданнями.
Пакети мають назву «Випробуй свою долю». Розподіляються завдання, як і на попередньому етапі.
2. Виконання учнями завдань.
Картка «Випробуй свою долю» (зразок)
-
Досліди функцію
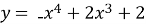 та побудуй її графік.
та побудуй її графік.
- Знайди область визначення функцій
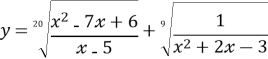
- Знайди число, яке в сумі зі своїм квадратом дає найменшу суму.
- Вікно має форму прямокутника, який зверху закінчується правильним трикутником. Периметр вікна дорівнює 3м. Якою повинна бути основа прямокутника, щоб вікно мало найбільшу площу?
3. Захист кожним з екіпажів своїх завдань. Один із представників екіпажу повністю наводить розв’язання текстової задачі, а інший надає «проспект не» розв’язання інших задач.
IV. Підсумок уроку.
Підраховується кількість балів, зароблених учасниками подорожі, з’ясовується, хто найуспішніший у країні Диференціального Числення.
V. Домашнє завдання.


про публікацію авторської розробки
Додати розробку