Презентація "Найбільше і найменше значення функції на проміжку".
Про матеріал
Цю презентацію можна використати для ознайомлення учнів зі знаходженням найбільшого і найменшого значення функції на заданому проміжку. Подібні задачі на пошук оптимального розв'язку займають значне місце в практичній діяльності людини. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
-
Дякую, що поділились.
-
pptx
До підручника
Алгебра і початки аналізу (профільний рівень) 10 клас (Мерзляк А.Г., Номіровський Д.А., Полонський В.Б., Якір М.С.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку


![Найбільшим значенням цієї функції на заданому проміжку буде f(-2)=4, а найменшим – f(0)=0. Це записують так: 𝑚𝑎𝑥𝑓𝑥=−2;1𝑓−2=4; 𝑚𝑖𝑛𝑓𝑥−2;1=𝑓0=0. Бачимо, що на заданому проміжку функція має точку мінімуму: х𝑚𝑖𝑛=0, але не має точок максимуму. Від найбільшого та найменшого значень функції, неперервної на проміжку, залежить і множина значень Е(f) на цьому проміжку. Так , множиною значень функції f(x)=𝑥2, заданої на проміжку хϵ−2;1, є множина Е(f)=[0;4] Отже, якщо m-найменше значення неперервної на проміжку [a;b] функції y=f(x), а М – найбільше значення, то множиною значень функції y=f(x) на проміжку [a;b] буде множина[m;M]. Найбільшим значенням цієї функції на заданому проміжку буде f(-2)=4, а найменшим – f(0)=0. Це записують так: 𝑚𝑎𝑥𝑓𝑥=−2;1𝑓−2=4; 𝑚𝑖𝑛𝑓𝑥−2;1=𝑓0=0. Бачимо, що на заданому проміжку функція має точку мінімуму: х𝑚𝑖𝑛=0, але не має точок максимуму. Від найбільшого та найменшого значень функції, неперервної на проміжку, залежить і множина значень Е(f) на цьому проміжку. Так , множиною значень функції f(x)=𝑥2, заданої на проміжку хϵ−2;1, є множина Е(f)=[0;4] Отже, якщо m-найменше значення неперервної на проміжку [a;b] функції y=f(x), а М – найбільше значення, то множиною значень функції y=f(x) на проміжку [a;b] буде множина[m;M].](/uploads/files/294516/231222/247112_images/2.jpg)
![Мал.1. Якщо на проміжку [a;b] функція має екстремуми, це не означає, що найбільшого або найменшого значення функція досягає в саме в точках екстремуму. Мал.1. На відрізку [a;d] найменшого і найбільшого значень функція набуває на кінцях проміжку [a;d], хоча має на цьому проміжку точки максимуму і мінімуму. Мал.2. На проміжку [b;d] найменшого значення функція досягає в точці мінімум. Мал.2. х1х2 Мал.1. Якщо на проміжку [a;b] функція має екстремуми, це не означає, що найбільшого або найменшого значення функція досягає в саме в точках екстремуму. Мал.1. На відрізку [a;d] найменшого і найбільшого значень функція набуває на кінцях проміжку [a;d], хоча має на цьому проміжку точки максимуму і мінімуму. Мал.2. На проміжку [b;d] найменшого значення функція досягає в точці мінімум. Мал.2. х1х2](/uploads/files/294516/231222/247112_images/3.jpg)
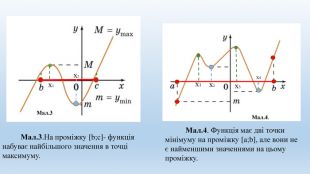
![Мал.3 Мал.3. На проміжку [b;c]- функція набуває найбільшого значення в точці максимуму. Мал.4. Функція має дві точки мінімуму на проміжку [a;b], але вони не є найменшими значеннями на цьому проміжку. Мал.4. х1х2х1х2х3х4 Мал.3 Мал.3. На проміжку [b;c]- функція набуває найбільшого значення в точці максимуму. Мал.4. Функція має дві точки мінімуму на проміжку [a;b], але вони не є найменшими значеннями на цьому проміжку. Мал.4. х1х2х1х2х3х4](/uploads/files/294516/231222/247112_images/4.jpg)
![Найбільше і найменше значення на відрізку та їх знаходження. Для функцій неперервних на замкненому проміжку має місце теорема Вейєрштраса: якщо функція у=f(x) визначена і неперервна на відрізку [a;b], то вона досягає на ньому найбільшого значення М і найменшого значення m.Інакше кажучи, на відрізку[a;b] знайдуться такі точки х1 та х2, що значення f(x1) і f(x2) будуть відповідно найбільшими і найменшими з усіх значень функції y=f(x) на цьому відрізку. Для знаходження найбільшого значення на відрізку достатньо знайти критичні точки, що лежать усередині відрізка;обчислити значення функції у цих критичних точках та на кінцях відрізка;з усіх отриманих значень функції вибрати найбільше і найменше. Найбільше і найменше значення на відрізку та їх знаходження. Для функцій неперервних на замкненому проміжку має місце теорема Вейєрштраса: якщо функція у=f(x) визначена і неперервна на відрізку [a;b], то вона досягає на ньому найбільшого значення М і найменшого значення m.Інакше кажучи, на відрізку[a;b] знайдуться такі точки х1 та х2, що значення f(x1) і f(x2) будуть відповідно найбільшими і найменшими з усіх значень функції y=f(x) на цьому відрізку. Для знаходження найбільшого значення на відрізку достатньо знайти критичні точки, що лежать усередині відрізка;обчислити значення функції у цих критичних точках та на кінцях відрізка;з усіх отриманих значень функції вибрати найбільше і найменше.](/uploads/files/294516/231222/247112_images/5.jpg)
![Розв’язування вправ. Приклад 24.1. Знайдіть найбільше і найменше значення функції на вказаному проміжку:f([)= 3𝑥2−𝑥3 , [-1;3]. Розв’язання.1. Знайдемо похідну функції. Маємо: f′(x)=(3𝑥2−𝑥3)′=3*2x-3𝑥2=6x-3𝑥2. 2. Знайдемо критичні точки функції. Для цього прирівняємо похідну до нуля. Маємо:6x-3𝑥2=0; 3х(2-х)=0. Звідси х1=0; х2=2. 3. Бачимо, що 0ϵ[-1;3] та 2ϵ [-1;3]. 4. Знайдемо значення функції на кінцях проміжка та в точках, що належать цьому проміжку.f(-1)=3-(-1)=4; f(3)=3*9-27=0; f(0)=0; f(2)=3*4-8=4. Отже, 𝑚𝑎𝑥𝑓𝑥=−1;3f(-1)=f(2)=4; 𝑚𝑖𝑛𝑓𝑥−1;3= f(0)=f(3)=0 -13х02 Розв’язування вправ. Приклад 24.1. Знайдіть найбільше і найменше значення функції на вказаному проміжку:f([)= 3𝑥2−𝑥3 , [-1;3]. Розв’язання.1. Знайдемо похідну функції. Маємо: f′(x)=(3𝑥2−𝑥3)′=3*2x-3𝑥2=6x-3𝑥2. 2. Знайдемо критичні точки функції. Для цього прирівняємо похідну до нуля. Маємо:6x-3𝑥2=0; 3х(2-х)=0. Звідси х1=0; х2=2. 3. Бачимо, що 0ϵ[-1;3] та 2ϵ [-1;3]. 4. Знайдемо значення функції на кінцях проміжка та в точках, що належать цьому проміжку.f(-1)=3-(-1)=4; f(3)=3*9-27=0; f(0)=0; f(2)=3*4-8=4. Отже, 𝑚𝑎𝑥𝑓𝑥=−1;3f(-1)=f(2)=4; 𝑚𝑖𝑛𝑓𝑥−1;3= f(0)=f(3)=0 -13х02](/uploads/files/294516/231222/247112_images/6.jpg)
![Самостійна робота.1234567123456788[-1;4][-2;2][-2;2][-2;2][-2;2][-2;2][-2;2][-2;2][-2;2]Знайдіть найбільше і найменше значення функції на заданому проміжку: Самостійна робота.1234567123456788[-1;4][-2;2][-2;2][-2;2][-2;2][-2;2][-2;2][-2;2][-2;2]Знайдіть найбільше і найменше значення функції на заданому проміжку:](/uploads/files/294516/231222/247112_images/7.jpg)