Конспект уроку "Числові нерівності"

Урок №5. Тема:  Числові нерівності

Формування компетентностей:

предметна компетентність:

• формування знань про числові нерівності;
• розвивати уміння порівнювати , здатність самостійно розв’язувати  задачі, підводити підсумки;

ключові компетентності:

• спілкування державною мовою – уміння доречно та коректно вживати в

мовленні математичну термінологію, чітко, лаконічно та зрозуміло формулювати думку; поповнювати свій словниковий запас;

• математична компетентність – уміння оперувати числовою інформацією;
• уміння вчитися впродовж життя – уміння оцінювати результати своєї

навчальної діяльності.

Тип уроку: засвоєння знань, вироблення вмінь.

Обладнання та наочність: підручник з алгебри за 9 клас, автори: Мерзляк, Полонський, Якір, 2017 р.

Хід уроку

I. Організаційний момент.

• Налаштовування на роботу.
•   Перевірка домашнього завдання: повідомлення балів за пройдений тест і розбір типових помилок.

II. Актуалізація опорних знань.

Фронтальне опитування

1. Які числа називають додатні?  Від’ємні?
2. Що таке координатна пряма?
3. Які знаки для порівняння чисел ви знаєте?
4. Який запис правильний: а) 3 < 5; б) 6 > 8; в) 0 < 1?
5.  Яке з чисел 1, 5, 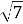, , 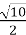-42,3 найбільше?

III. Вивчення нового матеріалу

Мотиваційна задача

Визначте, який із записів зайвий. Відповідь обґрунтуйте.

1. 25 > 17; 0,32 < 0,4; 0,5 = 1,4 – 0,9;
2. 25 > 17; 0,32 < 0,4; 0,5 < 1,4 – 0,9.

Після обговорення з учнями результатів виконання запропонованого завдання формулюється такий висновок: у 7 класі було вивчено питання про види, властивості й способи перетворення виразів, що не містять ділення на змінну (цілі вирази); у 9 класі настав час вивчити способи порівняння виразів. Цей висновок і є по суті основною дидактичною метою всього розділу

План вивчення нового матеріалу

1. Означення, що виражає залежність між співвідношеннями >, <, = і знаком різниці лівої та правої частин нерівно¬сті.
2. Види числових нерівностей.
3. Алгоритм доведення числових нерівностей.
4. Приклад доведення числової нерівності.

Опорний конспект

Означення: Два вирази, з’єднані між собою одним із знаків >, <,  ≥ , ≤ -  утворюють нерівність.

Означення. Число а більше від числа b, якщо а – b > 0; чис¬ло а менше від числа b, якщо а – b < 0.

3 цього означення випливає умова рівності двох чисел: число а дорівнює числу b, якщо а - b = 0.

Види числових нерівностей

Числові нерівності поділяють на такі види:

1. за знаком — строгі (а > b, а < b) і нестрогі (а ≥ b, a ≤ b);
2. за змістом — правильні (3 > 2) і неправильні (3 > 4).

Алгоритм доведення числових нерівностей

Щоб довести, що нерівність f(x) < g(x) (f(x) > g(x)) правиль¬на при будь-яких значеннях змінних, треба:

1. знайти різницю лівої та правої частин нерівності: f(x) – g(x);
2. перетворити (спростити, виділити повний квадрат тощо) різницю так, щоб можна було визначити її знак (< 0, > 0; = 0 );
3. скориставшись означенням, зробити висновок.

Приклад. Доведемо нерівність 

Доведення. Знайдемо різницю лівої та правої частин нерівності та перетворимо її:

Оскільки різниця лівої та правої частин нерівності дорівнює -4 < 0, то за означенням ліва частина менша від правої, тобто при будь-яких а.

IV. Засвоєння нових знань і способів дій

№1.2. Відомо, що . Чи може різниця дорівнювати числу:

1) 4,6;               2) –5,2;             3) 0?

№1.7.  Порівняйте значення виразів ) і при значенні що дорівнює: 1) –1; 2) 0; 3) 3. Чи можна стверджувати, що при будь-якому значенні b значення виразу більше за відповідне значення виразу

 ?

№1.8. Доведіть, що при будь-якому значенні змінної є правильною нерівність:

1)

2) ;

3) ;

4)

№1.16. Дано три послідовних натуральних числа. Порівняйте:

1. квадрат середнього із цих чисел і добуток двох інших;
2. подвоєний квадрат середнього із цих чисел і суму квадратів двох інших.

№1.20. Доведіть, що сума будь-яких двох взаємно обернених додатних чисел не менша від 231.

V. Підбиття підсумків уроку, рефлексія

В ході фронтального опитування разом з учнями підвести підсумки уроку. Запропонувати наступні питання:

• Сформулюйте означення нерівності
• Яка нерівність називається правильною
• Які властивості нерівностей ви знаєте

VI. Домашнє завдання
(§1 п.1 № 1.9, 1.17)