Конспект уроку для 5-х класів на тему: Розв'язування вправ. Самостійна робота з теми “Середнє арифметичне. Середнє значення величини»

Дата ___/___/___ Клас __________ Прізвище учителя _________________________

 

Урок № 106

Тема. Розв’язування вправ. Самостійна робота

Мета: систематизувати знання учнів щодо понять «середнє арифме­тичне», сформувати вміння учнів розв'язувати задачі високого рівня складності на застосування цих понять.

Тип уроку: узагальнення і систематизація навичок, знань і вмінь.

Ключова компетентність: на рух та його безпеку.

Хід уроку

І. Органiзацiйний етап

Привітання

▪ Перевірка присутності учнів: кількість за списком ______, кількість присутніх на уроці ________, відсутніх _______

▪ Перевірка готовності учнів та кабінету до уроку.

ІI. Перевірка домашнього завдання

• Перевірка завдання за підручником

№ 1244.

Відповідь:

№ 1247.

Відповідь: Середній виграш Олега складає х грн:

Відповідь: 48,75 грн.

• Усні вправи

1. Обчисліть:

1) 0,5 · 2,5 · 4 · 2; 2) 2 · 1,69 · 500; 3) 8,6 · 0,34 + 1,4 · 0,34;

4) 10,8 · 11,3 – 10,8 · 10,9.

2. Знайдіть значення виразу 6,5а + 0,035b, якщо:

1) а = 10; b = 1000; 2) a = 1; b = 1; 3) a = 0,1; b = 0; 4) a = 0; b = 0,2.

ІІІ. Узагальнення знань

• Запитання до класу

1. Сума 6 чисел дорівнює 45. Чому дорівнює їх середнє арифметичне?
2. Змішали 4,сорти цукерок за ціною 7,5 грн.; 8,4 грн., 9,5 грн., 10,6 грн. Скільки коштує 1 кг суміші, якщо взяли:

1) кожного сорту цукерок по 1 кг;

2) цукерок 1 і 3 сорту — по 2 кг; цукерок 2 і 4 сорту — по 1 кг?

3. Чи може середнє арифметичне двох десяткових дробів бути натураль­ним числом? Якщо так — навести приклад.

IV. Розв'язування задач

 Коментар. Оскільки поняття середнього арифметичного чисел і се­редньої величини (опрацьовані) осмислені учнями, на уроці розгляда­ються задачі високого рівня складності, розв'язання яких вимагає за­стосування понять про середнє арифметичне і середньою величину.

 

• Робота учнів з підручником біля дошки

№ 1251.

Для виготовлення сиру змішали 4 бідони молока різної жирності: 4,2 %, 4 %, 3,6 % та 3 %. Яку середню жирність молока одержали?

Відповідь:

Для самостійного виконання.

№ 1252.

Для приготування заправки до фруктового салату взяли по 100 г йогуртів жирністю 10 %, 3 % та 5 %. Йогурт якої жирності одержали в результаті змішування?

Відповідь:

Для самостійного виконання.

№ 1254.

Водій атобуса завжди дотримувався правил безпеки руху. За першу годину він проїхав 60 км, за другу й третю - у середньому по 61 км, а за четверту - на 10 км більше, ніж за першу годину. Скільки кілометрів у середньому за годину долав автобус?

Відповідь:

Для самостійного виконання.

№ 1255.

Відповідь:

Середній бал у команди «Чемпіон» складає х балів, тобто:

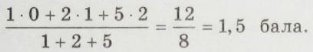
Відповідь: 1,5 бала.

• Умова Самостійної роботи з теми “Середнє арифметичне. Середнє значення величини»

 

Варіант 1

1. Купили 3 кг цукерок за ціною 50 грн., 68,4 грн. і 85,9 грн. Знайдіть середню ціну цукерок.

• 52,5 грн.;
• 68,1 грн.;  *
• 75,2 грн.;
• 34,8 грн..

Розв’язання:

(50 + 68,4 + 85,9) : 3 = 204,3 : 3 = 68,1 (грн.).

2. Перерви в школі тривають 5 хв., 10 хв., 20 хв., 15 хв., 10 хв. Яка середня тривалість перерви в школі?

• 14 хв.;
• 11 хв.; 
• 15 хв.; 
• 12 хв. *

Розв’язання:

(5 + 10 + 20 + 15 + 10) : 5 = 60 : 5 = 12 (хв.).

 

3. Оленка має такі результати зі стрибків у довжину: 2,9 м, 4,4 м, 3,5 м, 4,1 м. Обчисліть середній результат стрибка.

• 3,215 м;
• 3,725 м;  *
• 3,314 м;
• 3,435 м.

Розв’язання:

(2,9 + 4,4 + 3,5 + 4,1) : 4 = 14,9 : 4 = 3,725 (м).

4. У команді сім гравців. Двом із них по 10 років, трьом – по 11 років, а двом – по 12 років. Який середній вік гравців у команді?

• 11,5 років;
• 11 років;  *
• 12 років;
• 10,5 років.

Розв’язання:

(2 · 10 + 3 · 11 + 2 · 12) : 7 = (20 + 33 + 24) : 7 = 77 : 7 = 11 (років).

5. Автомобіль їхав 3 год. зі швидкістю 58,3 км/год і 2 год зі швидкістю 72,3 км/год. Знайдіть середню швидкість автомобіля на всьому шляху.

• 71,1 км/год.;
• 63,9 км/год.; *
• 52,1 км/год.;
• 67,4 км/год.

Розв’язання:

(3 · 58,3 + 2 · 72,3) : 5 = (174,9 + 144,6) : 5 = 319,5 : 5 = 63,9 (км/год).

6. Середнє арифметичне чисел 5,8 і х дорівнює 10,1. Знайдіть х.

• 14,4;  *
• 13,9;
• 22,5;
• 17,3.

Розв’язання:

(5,8 + х) : 2 = 10,1;

5,8 + х = 10,1 · 2;

5,8 + х = 20,2;

х = 20,2 – 5,8;

х = 14,4.

7. Із поля площею 4 га зібрали врожай пшениці 104,1 ц/га, а з поля площею 6 га зібрали 135,8 ц/га пшениці. Обчисліть середній урожай пшениці з 1 га.

• 123,12 ц/га; *
• 134,95 ц/га;
• 122,15 ц/га;
• 130,28 ц/га.

Розв’язання:

(4 · 104,1 + 6 · 135,8) : 10 = (416,4 + 814,8) : 10 = 1231,2 : 10 = 123,12 (ц/га).

8. Перше число в 1,5 рази більше за друге, а їх середнє арифметичне дорівнює 35. Знайдіть ці числа.

• 42 і 28;  *
• 70 і 35;
• 50 і 20;
• 40 і 30.

Розв’язання:

Нехай 1,5 · х – перше число, тоді х – друге число. Складаємо рівняння:

(1,5 · х+ х) : 2 = 35;

1,5 · х + х = 35 · 2;

2,5 · х  = 70;

х = 70 : 2,5;

х = 28. – друге число.

1,5 · х = 1,5 · 28 = 42. – друге число.

Варіант 2

1. Купили 3 кг печива за ціною 42,8 грн.,  53,2 грн і 72,3 грн. Знайдіть середню ціну печива.

• 70,4 грн.;
• 56,1 грн.;  *
• 67,3 грн.;
• 48,9 грн..

Розв’язання:

(42,8 + 53,2 + 72,3) : 3 = 168,3 : 3 = 56,1 (грн.).

2. Перерви в школі тривають 5 хв., 15 хв., 20 хв., 20 хв., 10 хв. Яка середня тривалість перерви в школі?

• 15 хв.;
• 12 хв.;
• 14 хв.;  *
• 11 хв.

Розв’язання:

(5 + 15 + 20 + 20 + 10) : 5 = 70 : 5 = 14 (хв.).

3. Павлик має такі результати зі стрибків у довжину: 3,9 м, 4 м, 3,7 м, 4,2 м. Обчисліть середній результат стрибка.

• 4,5 м;
• 4 м; 
• 3,95 м;  *
• 4,95 м.

Розв’язання:

(3,9 + 4 + 3,7 + 4,2) : 4 = 15,8 : 4 = 3,95 (м).

4. У команді п’ять гравців. Двом із них по 10 років, двом – по 11 років, а одному – 12 років. Який середній вік гравців у команді?

• 10,5 років;
• 10,8  років;  *
• 10 років;
• 11 років.

Розв’язання:

(2 · 10 + 2 · 11 + 12) : 5 = (20 + 22 + 12) : 5 = 54 : 5 = 10,8 (років).

5. Автомобіль їхав 3 год. зі швидкістю 44,2 км/год і 3 год зі швидкістю 62,4 км/год. Знайдіть середню швидкість автомобіля на всьому шляху.

• 81,1 км/год.;
• 53,3 км/год.; *
• 42,1 км/год.;
• 62,4 км/год.

Розв’язання:

(3 · 44,2 + 3 · 62,4) : 6  = (132,6 + 187,2) : 6 = 319,8 : 6 = 53,3 (км/год).

6. Середнє арифметичне чисел 4,4 і х дорівнює 12,8. Знайдіть х.

• 15,7; 
• 12,8;
• 21,2;  *
• 18,6.

Розв’язання:

(4,4 + х) : 2 = 12,8;

4,4 + х = 12,8 · 2;

4,4 + х = 25,6;

х = 25,6 – 4,4;

х = 21,2.

7. Із поля площею 3 га зібрали врожай пшениці 102,8 ц/га, а з поля площею 7 га зібрали 125,1 ц/га пшениці. Обчисліть середній урожай пшениці з 1 га.

• 120,2 ц/га;
• 118,41 ц/га;  *
• 112,5 ц/га;
• 134,28 ц/га.

Розв’язання:

(3 · 102,8 + 7 · 125,1) : 10 = (308,4 + 875,7) : 10 = 1184,1 : 10 = 118,41 (ц/га).

8. Перше число в 1,2 рази більше за друге, а їх середнє арифметичне дорівнює 42.  Знайдіть ці числа.

• 46 і 38;  *
• 50 і 53;
• 35 і 40;
• 70 і 84. 

Розв’язання:

Нехай 1,2 · х – перше число, тоді х – друге число. Складаємо рівняння:

(1,2 · х+ х) : 2 = 42;

1,2 · х + х = 42 · 2;

2,2 · х  = 84;

х = 84 : 2,2;

х ~38. – друге число. Або х ~38,2. Або х ~38,18.

1,2 · х = 1,2 · 38 ~ 46. – друге число.  Або 1,2 · х = 1,2 · 38,2 ~ 45,8. – друге число. 

Або 1,2 · х = 1,2 · 38,18 ~ 45,82. – друге число. 

V. Підсумок уроку

• Вправа « Заморочки з бочки» - на маленьких папірцях записати запитання, папірці закрутити та кинути в коробку у вигляді бочки. Учні по черзі витягують запитання та дають на них відповіді.

VI. Домашнє завдання

Завдання для всього класу: § 34 (повторити), розв’язати № 1250, № 1253. – стор. 226-227,

§ 19 (повторити).