Конспект уроку "Формула коренів квадратного рівняння"

Конспект уроку алгебри, 8 клас,             

Тема:   Формула коренів квадратного рівняння

Мета: Освітня: закріпити означення квадратного рівняння, формули дискримінанта квадратного рівняння та формул коренів квадратного рівняння; вдосконалити вміння відтворювати вивчені означення і формули та використовувати їх для розв'язування завдань; відпрацювати вміння розв'язувати квадратні рівняння за формулами;

Розвиваюча: розвивати розумову діяльність та комунікативні навички учнів; розвивати пізнавальні інтереси;

Виховна: виховувати самостійність, намагатися скласти ситуацію успіху для кожного учня.

Тип уроку: урок застосування знань і вмінь.

Обладнання та наочність: роздавальний матеріал, індивідуальні таблички «квадрати натуральних чисел», правила проведення інтерактивних вправ «Карусель» та «Поспішай та не помились».

Епіграф: Про глибину ідеї, закладеної в формулюванні нового математичного поняття, можна робити висновок лише згодом за тим, наскільки вміло вдається використати це поняття.

Вігнер Ю.

ХІД УРОКУ:

I. Організаційний етап

Оноре де Бальзак сказав, щоб дійти до мети, треба найперше йти. Ми також будемо йти до своєї мети, відтворивши перш за все матеріал попередніх уроків.

Рівняння, рівняння, рівняння -

На кожному кроці вони.

Тобі допоможуть із складної ситуації

Вихід правильний знайти!

Вони, мов той ключик чарівний,

Відкрили світ дивний-предивний,

Усім допомогли зрозуміти,

Що з ними потрібно дружити.

Чи дружите ви з рівняннями домашніх завдань?

II. Перевірка домашнього завдання

1) Перевірка завдання заданого за підручником

Два учні біля дошки відтворюють ті завдання, які для більшості дітей показалися найважчими.

2) Перевірка додаткового завдання

З місця один з учнів пояснює розв’язання додаткового завдання.

III. Актуалізація опорних знань і вмінь

Яку тему ми вивчали на попередньому уроці? (Квадратні рівняння. Формула коренів квадратного рівняння.) Тож давайте пригадаємо, що ми вивчили.

Індивідуальне опитування:

-Рівняння, що має вигляд ах² + bх + с = 0, де х - змінна,   a, b, c - довільні числа, причому а не дорівнює нулю, називають…

 (квадратним)

-Вираз b² – 4aс називають … квадратного рівняння

 (дискримінантом)

-Якщо у квадратному рівнянні перший коефіцієнт дорівнює 1, то його називають…

 (зведеним)

-Квадратне рівняння називають ще рівнянням другого…

( степеня)

-Якщо дискримінант квадратного  рівняння дорівнює нулю, то рівняння має один…

 (корінь) 

-Якщо хоча б один з коефіцієнтів b або c квадратного рівняння дорівнює нулю, то рівняння називають…

 (неповним)

-Для обчислення коренів квадратного рівняння існує…

( формула)

-Якщо значення виразу b² – 4aс є від'ємним числом, то рівняння не має

…  коренів

( дійсних)

-Число а в квадратному рівнянні називають першим….

( коефіцієнтом)

-Квадратне рівняння має два корені, якщо дискримінант є …. числом

( додатним)

-Який термін з латинської мови перекладається як «розрізняючий»

 ( дискримінант)

 

Виконання усних вправ

 

1. Укажіть у квадратному рівнянні його коефіцієнти:

а) 3у² – 5у + 1 = 0;

б) -х² + х – 3 = 0;

в) 12t – 7t² + 4 = 0;

г) 9t – 6 + t² = 0;

д) 5т – т² = 0;

є) п² – 7 = 0.

2. Спростіть вирази:

;                (2k)² – 4ат.

3. Скільки коренів має квадратне рівняння:

x² – 64 = 0;     у² + 49 = 0;    2р² – 7р = 0;     k² = 0; 2х² + 4х – 1 = 0;

х² + 3х + 4 = 0;       у² + 3у + 2= 0.

IV. Формування вмінь та навичок

Ми сьогодні з вами продовжимо вивчати тему квадратні рівняння, а саме зупинимося на вивченні формул коренів квадратного рівняння, якщо другий коефіцієнт парне число.

Якщо другий коефіцієнт квадратного рівняння - парне число, тобто b = 2k, то при розв’язуванні квадратного рівняння можна користуватися формулою: 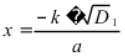, де , .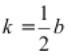

Виконання письмових вправ

1. Інтерактивна гра « Поспішай та не помились»

Учитель по черзі вивішує завдання за завданням, для кожного з варіантів, а учні на аркушах – трафаретах пишуть відповіді.

Варіант 1	Варіант 2
1. У квадратному рівнянні підкресліть однією лінією старший коефіцієнт, двома лініями - другий і трьома - вільний член:
а)2х² + 3х -4 =0; б) 13х -5х² +1=0; в) 12+ х² -5х=0; г) х² + 4=6х;	а) 4х² -2х+5=0; б) 11-2х² +4=0; в) 14-х² -2х=0;  г) 7х -х² =5;
2. Складіть квадратне рівняння ах² +bх +с=0, в якому:
а) а=1, b=-2, с=3; б) b=4, а=-1, с=4; в) с=-5, а=2, b=-1; г) b=0, с=9, а=-1.	а) а=2, b=-1, с=5; б) b=-5, с=3, а=-1; в) с=-4, b=2, а=-3; г) с=0, а=5, b=-3.
3. Виділіть квадрат двочлена:
4х² + 20х + 31;	9х² + 24х+20;
х² +14х+25	х² + 10х +16

 

Підводиться підсумок виконання завдань.

 

2. Розв'язування квадратного рівняння за формулами.

(Учні по черзі виходять до дошки і під керівництвом учителя розв’язують рівняння)

1) Розв'яжіть рівняння:

а) х² – 2х – 1 = 0;

 б) 7х² – 18х + 8 = 0;

в) 3х² + 22х – 16 = 0;

г) х² + 21х + 90 = 0;

д) 3х² + 53х – 18 = 0;

є) -25х² + 50х + 75 = 0;

ж) х² + 0,5х – 1,5 = 0;

з) 2х² – х + = 0;

2) Розв'яжіть рівняння:

а) 3х² – 14х + 16 = 0;

б) 5х² – 16х + 3 = 0;

в) х² + 2х – 80 = 0;

г) х² – 22х – 23 = 0;

д) 4х² – 36х + 77 = 0;

є) 15у² – 22у – 37 = 0;

ж) 7z² – 20z + 14 = 0;

з) у² – 10у – 25 = 0.

3. Розв'язування рівнянь з попереднім виконанням рівносильних пе­ретворень та обранням найбільш зручного способу розв'язання.

1) Розв'яжіть рівняння:

а) t² + 3t = - 4t – 6 – t²;                     б) 5(y² + 3) = -24у + 20;

в) 4х(х – 2) + х² = 6х + 3;                   г) 6х² + 3х = 5(2х + 1);

д) (х – 1)² + 4х² = 0;                            е) (3х – 2)(3х + 2) = 6х + 3;

ж) 5х² – х = 0,1 – х + 4х²;            з) .

2) Знайдіть корені рівняння:

а) 3(х + 4)² = 10х + 32;              б) 15х² + 17 = 15(х + 1)²;

в) (x + 1)² = (2х – 1)²;                 г) (х – 2)² + 48 = (2 – 3х)².

3) Розв'яжіть рівняння:

а) ;                    б) ;

в) ;               г) .

 

V. Систематизація та узагальнення знань учнів

1. Виконання усних вправ

Розкладіть на множники:

x²-81;    а²+10a+25;    4a-12;    4а³-16a;     а³+2а²+а.

2. Повторення теоретичних знань із використанням інтерактивної  вправи « Карусель»

Учні сидять у двох колах обличчям один до одного. Внутрішнє коло нерухоме, а зовнішнє рухається. Вчитель вивішує на дошці завдання, учні розв’язують його в парах ( як сидять - один навпроти одного ). За сигналом вчителя відбувається зміна партнерів, і робота продовжується вже у складі інших пар. Учитель контролює роботу.

Завдання

1.) Розкладіть на множники многочлен:

1) 2х²-18;

2) 4х²+4х+1;

3) х²-5х+6.

2.) Знайдіть корені квадратного тричлена:

1) х²-5х+6;

2) х²-5х;

3) 3х²-4х+1.

3.)  Скільки коренів має рівняння:

1) х² – 10х + 25 = 0,

2) х² + 6х + 9 = 0

3) х² + 5x – 14 = 0;

4) 3у² – 3у + 4 = 0;

5) 25х² + 60х + 36 = 0?

(По закінченні вправи підводиться підсумок)

VI. Підсумки уроку

Прес – конференція. Обговорення того, наскільки повно було виконано роботу на уроці  , в якому напрямку необхідно працювати далі.

Отже, в результаті активної праці сьогодні на уроці кожен учень з впевненістю може сказати:

Рівняння – це не просто рівність

З однією змінною чи кількома.

Рівняння – це думок активність,

Це інтелекту боротьба.

Виставлення оцінок

VII. Домашнє завдання

Основний рівень

Повторити § 19, № 644, 646, 648

Високий рівень

Додатково № 660(1)

(за підручником: А.Г. Мерзляк, В.Б. Полонський, М.С. Якір. Алгебра. Підручник для 8 класу — 2016 р.).