Конспект уроку " Лінійні нерівності з однією змінною з використанням платформи Мійклас"

Тема уроку. Лінійні нерівності з однією змінною.

 

Мета уроку: систематизувати і узагальнити знання учнів по темі, продовжити формувати практичні навики по розв`язуванню нерівностей; на прикладах показати учням застосування нерівностей до практичних задач; розвивати підприємливість та фінансову грамотність, логічне мислення; вчити учнів працювати як з підручником так і на освітніх платформах.

 

Тип уроку: урок узагальнення та систематизації знань з використанням матеріалів платформи Мійклас.

 

Обладнання: таблиці зі схемами, роздатковий матеріал, індівідуальні гаджети з підключенням до інтернету, ноутбук вчителя.

 

Хід уроку

1. Теоретична розминка.

1.Правило порівняння двох довільних чисел.

2. Сформулювати теореми, які виражають властивості числових нерівностей.

3. Що називається розв`язком нерівності? Що означає розв’язати         нерівність?

 4. Які нерівності називаються рівносильними?

 5. Сформулювати властивості, які використовуються при розв’язуванні    нерівностей.

 

 2. Усний рахунок.

 

1) Відомо, що  3 < a < 4.  Оцінити   3a   

 

2) Знаючи, що  4 < x < 5;  1 < y < 2  Оцінити  x + y;  x - y

 

3) Зобразити на координатні прямій проміжок [ -3; 6]   (7; 10) 

 

4) Які з цілих чисел належать проміжку ( -4; 0)

 

Зміст миттєвого тесту.

 

1. Яка з нерівностей правильна?

 А) – 10 > - 7; Б) 5,3 > - 5,4; В) – 6,5 > 0;  Г) 0 > 3,6.

 

2. Які з неведених чисел є розв`язками нерівності 10x + 1> 11?

      А) 1;      Б) 0;     В)  - 3;     Г) 1,2.

 

3. Які з неведених чисел є розв`язками нерівності  (x + 7)(x – 10) > 0?

      А) – 7;     Б) 11;    В) 5;     Г) – 5.

 

Учні класу працюють над тестовими завдання, виконуючи попередньо необхідні обчислення в зошиті. Вчитель постійно здійснює контроль. Для цього після виконання завдання учні піднімають картки з буквами правильної відповіді. Комплект букв А, Б, В, Г  є у кожного учня.

 

3. Перевірка виконання домашнього завдання.

Домашнє завдання учні виконували на платформі Мійклас.

 

       На уроці вчитель вже має результати всіх учнів, і  аналізує основні помилки які були допущені в перевірочній роботі за темою «Властивості числових нерівностей».

 

 

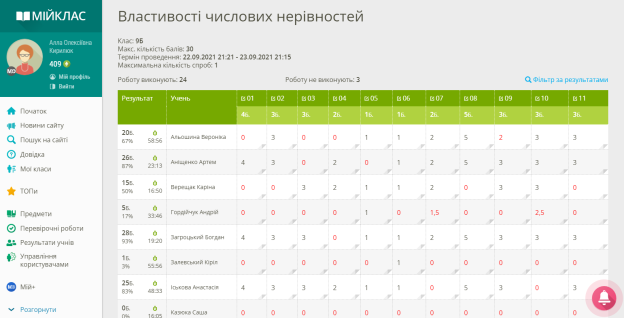
1. Відомо, що k<6,t<8

Оцінити значення виразу 4k+5t.

 

2. Відомо, що b>c.

  

Правильними нерівностями є:

  

Можливі кілька правильних варіантів відповідей.

 

• 7,31−b>7,31−c
• 7,31b>7,31c
• b+7,31>c+7,31
• b−7,31>c−7,31
• −7,31b<−7,31c

 

 

3)Обери нерівності, на основі яких можна стверджувати, що a>b.

 
 

• a−11>b−11
• a7>b7
• 2a>2b
• 14−a>14−b
• −2a>−2b

 

4.Розв’язування тренувальних вправ.

 

 

    1. Відомо, що  15 < a < 25.     Оцінити значення виразів

    а)  0,2a  +  3;          б) 6 – 2a

 

   2. Знаючи, що    2 < x < 4;  1< y < 3.   Оцінити

     а) 2x – 3y;           б) 4xy

 

   3. Розв`язати нерівності

     а)  5x + 7 < 3x + 1;          б) 4x – 2 > 7x + 1

 

5.Робота з підручником : №5.23,  5.26,  5.28. А.Г. Мерзляк

 

  В кінці уроку вчитель вибірково збирає зошити  учнів для перевірки.

 

6. Розв’язування прикладних задач з використанням нерівностей.

 

      На мові нерівностей розв`язується багато практичних задач. До них належать так звані задачі оптимізації. Тобто це є пошук найкращого варіанту у вирішенні того чи іншого завдання. Це є задачі на знаходження найбільш вигідних варіантів перевезень на транспорті, способів розкрою тканини, деревини, металу, пластмаси та інше, знаходження найбільш ефективних режимів роботи підприємств.

      Учні знайомляться з найпростішими задачами оптимізації. 

 

 

1. Маса чавунної заготовки 16 кг. Яку найменшу кількість таких заготовок треба взяти щоб відлити 41 деталь масою 12 кг кожна?

 

2. З дроту, довжина якого 10 м, виготовляють обручі, завдовжки 45см. Яку найбільшу кількість обручів можна виготовити?

 

3. Зі складів А і Б потрібно привести 60 комплектів меблів до магазину. Відомо, що перевезення одного комплекту зі складу А в магазин коштує 70 гривень, а зі складу Б – 40 гривень. Яку найбільшу кількість меблів можна вивантажити на складі А якщо на перевезення меблів до магазину виділяється 2800 гривень?

 

4. Фермерське господарство виділило під кормові культури 100 га. Вирішили використати цю землю під посіви кукурудзи і цукрового буряка. Як розподілити площу між цими культурами, якщо врожайність кукурудзи 500 ц з гектару, а буряка – 200 ц з гектару, що зібрати не менше 32 000 ц врожаю? Яка найменша площа може бути засіяна кукурудзою? 

 

Вчитель працює з учнями класу.

Учні які були визначені як «сильна ланка», розв`язують самостійно індивідуальні завдання . Інша група учнів, що розв’язували вже запропоновані задачі оптимізації, складають самостійно подібні задачі. Якщо складно це виконати, то розв’язують ще одну із класних задач.

 

6. Самостійна робота.

 

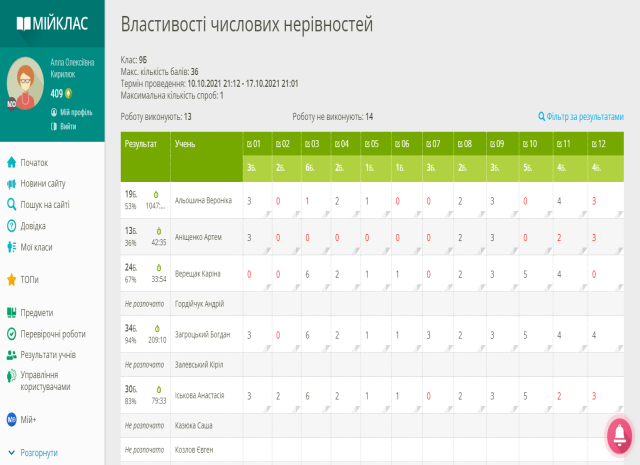
Як підсумок урок , самостійну роботу вчитель пропонує виконати  знову ж на платформі Мійклас. Учні використовують власні гаджети і кожен виконує свій варіант. Вчитель на ноутбуці стежить за роботою учнів та  надає індивідуальні коментарі.

 

 

 

7. Підсумок уроку.

 

     Проаналізувати разом з учнями, що було зроблено для досягнення мети уроку.

 Оголосити оцінки за знання теоретичного матеріалу ; за кращу роботу під час тестів.

Результати виконання самостійної роботи учні автоматично отримують на платформі Мійклас.

 

8. Домашнє завдання.

 

Учні виконують письмові диференційовані завдання зі збірника дидактичних матеріалів під редакцією А.Г.Мерзляка.