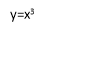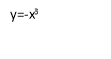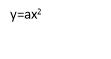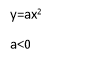Система уроків з теми «Квадратична функція» із застосуванням інтерактивних методів та опорних схем. 9 клас

Про матеріал

Найбільш ефективним при вивченні теми «Квадратична функція» вважаю застосування прийому розподілу навчального матеріалу на окремі частини – опорні блоки та опорні схеми. Зорове сприйняття матеріалу дає можливість учню краще засвоювати необхідну інформацію та легко справлятися із практичними завданнями. Тому пропоную розподілити матеріал на окремі блоки, використовуючи підручник алгебри для 9 класу (А.Мерзляк, В.Полонський, М.Якір; Х «Гімназія» 2017) :

Перегляд файлу

Система уроків з теми «Квадратична функція» із застосуванням інтерактивних методів та опорних схем. 9 клас

Функція – одне з найважливіших понять сучасної математики. Воно створювалося і збагачувалося протягом кількох тисячоліть. В основній щколі поняття «функція» реалізує такі основні завдання як формування системи функціональних понять, уміння використовувати функції та їх графіки для характеристики залежностей між величинами, опису явищ та процесів.

Тому пропоную розподілити матеріал на окремі блоки, використовуючи підручник алгебри для 9 класу (А.Мерзляк, В.Полонський, М.Якір; Х «Гімназія» 2017) :

направляючий блок включає завдання на організацію пізнавальної діяльності;
блок самоперевірки допомагає учням перевірити рівень засвоєння матеріалу;
контрольно-узагальнюючий блок дозволяє визначити рівень засвоєння основного змісту теми;
розширювальний блок носить творчий характер, вимагає глибоких знань і вміння використовувати їх у новій навчальній ситуації.

Крім того , слід структурувати навчальний матеріал.

Пропоную орієнтовну структуру навчального матеріалу при вивченні теми «Квадратична функція».

МЕТА	ТЕХНОЛОГІЯ
НАПРАВЛЯЮЧИЙ БЛОК
Урок ознайомлення з новим матеріалом (ознайомлення учнів з особливостями методики складання опорних схем)	Ситуаційна технологія
Урок вивчення нового матеріалу (Опорні схеми створюються разом з учнями)	Технологія евристичного мислення
Урок фронтального опрацювання матеріалу (навчання учнів згортати інформацію у схеми)	Технологія укрупнення дидактичних одиниць
БЛОК САМОПЕРЕВІРКИ
Урок колективного опрацювання матеріалу (робота над опорними схемами)	Технологія інтерактивного навчання
Урок індивідуального опрацювання матеріалу (самостійне складання опорних схем)	Технологія рівневої диференціації
КОНТРОЛЬНО-УЗАГАЛЬНЮЮЧИЙ БЛОК
Урок систематизації знань та вмінь (практичне застосування опорних схем)	Технології використання опорних схем та моделей
РОЗШИРЮВАЛЬНИЙ БЛОК
Урок контролю знань та вмінь	Технології вузівського навчання

В направляючий блок включають завдання на організацію пізнавальної діяльності, які спонукають учнів до активної розумової праці. Наведу приклади складання опорних схем і таблиць на окремих уроках з теми «Квадратична функція».

Тема: Функція. Властивості функцій Мета уроку: формувати уміння будувати та аналізувати графіки функцій; характеризувати за графіками функцій процеси, які вони описують.

Очікувані результати: учні повинні відтворити знання за 7-8 клас по вивчених темах «Функція»; вміти будувати графіки відомих функцій та формулювати їх властивості

Основні поняття:функція,графіки відомих функцій, властивості функцій.

Компетентності, що формуються:математична-вміти будувати та аналізувати графіки функцій;

уміння вчитися-самоорганізуватись до навчальної діяльності;

спілкування державною мовою-розпізнавати проблему, міркувати, робити висновки на основі інформації поданої в графіках;

соціальна-розвивати вміння працювати в колективі;

інформаційна-навчати учнів використовувати таблиці, малюнки як джерело інформації

Обладнання: підручник, роздавальні матеріали, мультимедійний супровід.

Тип уроку: урок систематизації знань та вмінь.

Хід уроку

І. Організаційний момент.

II. Формулювання теми, мети й завдань уроку. Мотивація навчальної діяльності

Епіграф: «Єдиний шлях, що веде до знань-діяльність»

Проводиться обговорення епіграфа. Із різних думок пропонується висновок: щоб отримати знання , потрібно діяти.

Вчитель знайомить учнів із структурою навчального матеріалу при вивченні теми «Квадратична функція»; оголошує тему, мету уроку ; надає рекомендації основних прийомів роботи з опорними схемами та конспектами; пропонує діяти

ІІI.Сприйняття та усвідомлення нового матеріалу

Опорні знання: Відтворення знань з теми «Функція» за 7-8 класи.

Використовуючи інтерактивні вправи «Пошук інформації», «Синтез думок», «Шпаргалка», фронтальну бесіду, учні пригадують раніше вивчений матеріал:види функцій, їх графіки та властивості.

Фронтальна бесіда:

Що таке функція?
Як називають змінну х, змінну у?
Що таке область визначення ? Область значення?
Які існують способи завдання функції?
Пригадайте формули знайомих функцій та їх графіки.

В процесі обговорення теми уроку складається опорна схема.

ВИДИ ФУНКЦІЙ

- лінійна функція

2.emf Графік – пряма.

$C:\Documents and Settings\User\Рабочий стол\temp\1.emf$

2.emf 1.emf

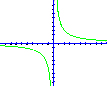
Обернена пропорційність.

Графік – гіпербола.

3.emf 3.

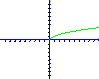
Графік – одна вітка параболи.

1.emf 2.emf 4.

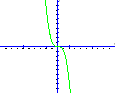
Графік – кубічна парабола.

1.emf

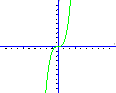
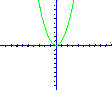
Графік - парабола

3.emf a>0

За схемою учні повторюють усі властивості вивчених функцій.

IṾ. Осмислення нового матеріалу: учні ознайомлюються із таблицею підручника( ст. 60) Вчитель проводить бліцопитування по вивченому матеріалу.

V.Домашнє завдання: відтворити зміст конспекту, виконаного за підручником, і звірити його з конспектом у зошиті;розв’язати 7.2, 7.7, 7.11.

Тема: Перетворення графіків функцій.

Мета уроку:домогтися засвоєння правил перетворення графіків функцій

формувати вміння будувати графікі функцій, застосовуючи відповідні перетворення.

Очікувані результати:учні повинні знати правила та уміти будувати графіки функцій, застосовуючи відповідні перетворення.

Основні поняття:графік функції, паралельне перенесення вздовж осі, осьова симетрія.

Компетенції, що формуються:

математична-уміння застосовувати правила перетворення графіків функцій при розв’язуванні задач, що передбачають побудову;

спілкування державною мовою-розвивати вміння відтворювати інформацію словесно, формулювати та аргументувати свої думки;

соціальна-вчитись працювати в команді,аналізувати отримані дані з точки зору власного досвіду;

інформаційно-цифрова-розвивати просторове уявлення, вчитись моделювати графіки за допомогою прикладних програм.

Обладнання:підручник, роздаткові матеріали, мультимедійний супровід.

Тип уроку: засвоєння нових знань і вмінь.

Хід уроку

І. Організаційний момент.

II. Перевірка домашнього завдання.

1) Гра-сюрприз: учням пропонуються лотерейні білети (15шт).В коробці по три білети із формулою однієї функції; в кожному із трьох- різні завдання, але вони разом складають повну відповідь на одне запитання, наприклад : Опишіть функцію у=2х; Побудуйте графік функції у=2х; Сформулюйте властивості функції у=2х».

Учням необхідно об’єднатись у групи по троє, підготуватись і дати повну відповідь.

III.Формулювання теми, мети й завдань уроку; мотивація навчальної діяльності.

Вчитель перевіряє виконані завдання, коментує відповіді. Далі говорить про те, що дослідження функції за готовим графіком є більш простим, ніж за формулою. Розвиваючи цю думку, повідомляє учням, що розв’язання деяких задач передбачає побудову графіків функцій, які не є елементарними( вчитель наводить приклади).

Проблемне запитання: Чи є способи, за допомогою яких можна побудувати графік будь-якої функції, використовуючи вміння будувати графіки елементарних функцій?

Пошук відповіді є метою уроку.

IV. Сприйняття та усвідомлення нового матеріалу

Вивчення нового матеріалу подається за планом з мультимедійним супроводом.

Вчитель демонструє побудову графікау=

1.Побудова графіка у=;

2.у= (графік функціїу= переміщується вправо на 3 одиниці вздовж осі Ох);

3. у=(графік функції у= переміщується на 2 одиниці вверх вздовж осі Оу)

Після завершення побудови узагальнюються правила побудови графіків функцій за допомогою геометричних перетворень і на прикладі функції навчальний матеріал відображається в опорних схемах.

Перетворення графіків функції

2.emf

Графіки функцій

симетричні відносно осі ОХ

1.emf

, де k>0

розтягується відносно осі ОХ у k разів (ІІІ);

графік функції

стискається в разів до осі ОХ (ІІ)

4.emf

Графіки функцій рухаються відносно т.0 по осі ОY:

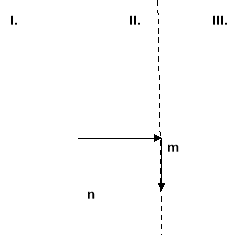
І. n>0 – вверх відносно т.0 на n одиниць.

ІІ. n<0 – вниз відносно т.0 на n одиниць.

5.emf

Графіки функцій рухаються відносно т.0

по осі ОY:

І. Вправо на на m одиниць, якщо m>0.

II. Побудуйте, Вліво на на m одиниць, якщо m<0.

V. Осмислення нового матеріалу

Самостійна робота

Завдання: Перетворити графіки заданої функції за формулами та властивостями, які вивчалися на уроці.

І варіант: Функція

ІІ варіант: Функція

VI. Підбиття підсумків

Рефлексія

VII Домашнє завдання

Опрацювати конспект уроку, скласти таблицю; завдання на встановлення відповідності ( «Повний курс математики в тестах» Ю.О. Захарійченко, ст.98, №57,58)

Тема: Квадратична функція та її властивості.

Мета:сформувати поняття квадратичної функції; формувати вміння будувати графік квадратичної функції.

Очікувані результати:розпізнавати квадратичну функцію серед інших елементарних функцій; знаходити координати вершини та напрям віток графіка квадратичної функції за формулою;виконувати побудову за вивченим алгоритмом.

Основні поняття:квадратична функція, парабола,вершина параболи, вісь симетрії параболи.

Компетентності, що формуються:математична-уміння застосовувати набуті знання до побудови графіка квадратичної функції;

спілкування державною мовою-розвивати вміння грамотно висловлюватися, коректно вживати математичну термінологію;

ініціативність і підприємливість-вміння аргументувати та захищати власну позицію, проявляти ініціативу.

Обладнання:підручник, роздавальні матеріали, мультимедійний супровід;

Тип уроку: засвоєння нових знань і вмінь.

Хід уроку

І. Організаційний момент.

Вчитель наголошує, що опорні схеми, які вивчались на попередніх уроках, послідовно розкривали тему «Квадратична функція».

ІІ. Перевірка домашнього завдання

Учням пропонується відтворити на окремих прикладах (приклади наводять школярі) основні етапи перетворень графіків функцій:

III. Актуалізація опорних знань

Інтерактивна вправа: «Мозковий штурм»

Що таке функція?

Що таке область визначення? Область значень?

Як знайти нулі функції?

Що таке проміжок знакосталості?

Яку функцію називають зростаючою на деякому проміжку? Спадною?

Як побудувати графік функції y=kf(x) y=f(x)+b y=f(x+a) y=-f(x)

IV. Формулюваннятеми, мети й завданьуроку.Мотивація навчальної діяльності.

На етапі вивчення нового матеріалу з метою розумової та пізнавальної діяльності вчителем ставиться проблемне запитання: Як побудувати графік функції , спираючись на раніше вивчений матеріал?

Використовуючи метод бесіди, взаємних запитань, із попереднім самостійним опрацюванням тексту підручника, учні розкривають суть проблеми і пропонують побудувати графік квадратичної функції , виділивши квадрат двочлена.

Матеріал узагальнюється у вигляді опорної схеми.

КВАДРАТИЧНА ФУНКЦІЯ

1. Функція виду , де b,c – довільні числа, а х – аргумент називають квадратичною.

2. Графіки і - однакові параболи, які можна сумістити паралельним перенесенням.

Побудова графіка

у=(х-m)²–n, у=а(х-m)²-n

1-й спосіб

A(x₀;y₀) – вершина параболи, де

Отже, схема побудови шуканого графіка є такою:

Паралельно перенести графік функції у=х² вздовж осі ОХ на m=x₀ одиниць вправо;
Паралельно перенести графік функції у=(х-m)² вздовж осі ОY на n=y₀ одиниць вниз;
При а>1, графік функції стискаємо до осі параболи в a разів/

1.emf

II.Вчитель пропонує інший спосіб побудови графіка квадратичної функції та узагальнює його у вигляді опорної схеми.

2-й спосіб:

Знайти координати вершини параболи A(m;n).
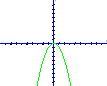
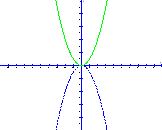
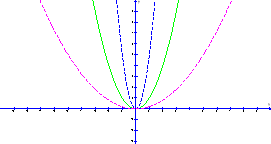
Визначити напрям віток параболи: a>0 – вітки напрямлені вверх, a<0 – вітки напрямлені вниз.
З ОДЗ знайти точку з координатами, побудувати її симетрично.
Позначити точки на координатній площині, провести через них плавну лінію.

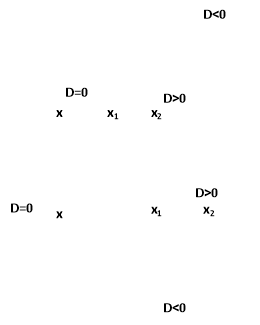
5. Вигляд графіка функції залежно від D, .

2.emf

a>0

3.emf

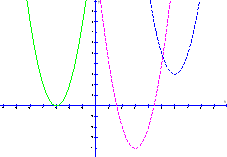
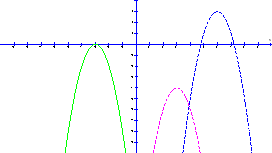
a<0

V. Сприйняття та усвідомлення нового матеріалу

1. Робота з підручником

Учні під керівництвом учителя опрацьовують підручник (рис11.1, 11.2)

VI.Осмислення нового матеріалу

1. За підручником самостійно учні опрацьовують приклад( ст100-101)

2. Розминка  гра « так чи ні»

- Функція- це правило,за яким кожному аргументу ставиться у відповідність декілька значень функції ні

- Функцію можна задати тільки описово ні

- Незалежну змінну називають аргументом так

- Область визначення функції y=7х-15 ,всі числа крім 0 ні

- Для функції y=-2х-5 f(1)=0 ні

- y=ах+в квадратична функція ні

- Вітки параболи квадратичної функції напрямлені вниз, якщо а>0

Ні

тА(m n)-вершина параболи так

VII.Підбиття підсумків

Продовжіть речення:сьогодні на уроці я зрозумів(ла)…

Сьогодні на уроці я навчився(лась)…

VIII. Домашнє завдання:

1. Запропонувати свій спосіб побудови графіка квадратичної функції

2. Опрацювати п11(підручник)N 11.3, 11.7. 11.9

3.У вайбер- групу скиньте свої враження про засвоєння вивченого матеріалу (смайлики).

Завдання блоку самоперевірки - допомогти учням перевірити рівень засвоєння нового матеріалу. На уроках учні відтворюють набуті знання, які подані в опорних схемах, та вчаться застосовувати їх при розв’язуванні вправ. Методи та прийоми роботи з опорними схемами:

відтворення матеріалу за готовою схемою (малюнок на дошці);
усне опитування по опорних схемах;
письмова перевірка узагальнених знань;
домашня та індивідуальна робота з опорною схемою;
практичне закріплення нового матеріалу (навчити прийомам роботи із опорними схемами, виконання тренувальних вправ).

Завдання контрольно-узагальнюючого блоку – дозволити учням визначити рівень засвоєння основного змісту теми. Вчитель підбирає такі вправи, які дозволяють учню дати впевненість у тому, що в навчанні він досягне успіху, тобто вчить вчитися. З метою організації пізнавальної і творчої діяльності учнів на уроках можна практикувати КВК, уроки-змагання, «Математичний бій», уроки-практикуми з елементами досліджень, уроки-семінари.

Форми роботи: індивідуальні, парні, групові та колективні.

Завдання розширювального блоку носять творчий характер, вимагають глибоких знань та вміння використовувати їх у новій навчальній ситуації. Використані технології на цьому етапі вивчення теми направлені на пізнавальну і творчу діяльність учнів. Однак, перевагу слід надавати індивідуальному та диференційованому підходам у навчанні.

Учням пропонуються такі опорні схеми:

ПОБУДОВА ГРАФІКІВ КВАДРАТИЧНОЇ ФУНКЦІЇ

З МОДУЛЯМИ

Побудувати графік функції .
Частина графіка над віссю ОХ – без змін, а частина графіка III I IV чверті симетрично відображається у верхню півплощину.

Приклад:

Графік складається з двох частин: - права півплощина, - ліва півплощина.

Графіки симетричні відносно ОУ.

Приклад:

Графік залежностей складається з графіків двох функцій і .

Частина графіка, що лежить над віссю ОХ, залишається без змін і ця сама частина симетрично відображається відносно осі ОХ.

Приклад:

На уроках розглядаються побудови графіків функцій виду:

[1. ст.127]

Використання геометричного змісту модуля (при )

Узагальнення

Матеріали розширювального блоку можна розглядати на факультативних заняттях.

Пропоновані опорні таблиці при вивченні теми «Квадратична функція» не є обов’язковими. Однак, в роботі утворюється значний резерв часу для виконання завдань, спрямованих на відпрацювання прийомів навчальної діяльності.

docx

Завантажити

Зберегти на потім

Додав(-ла)

Іванченко Лариса Володимирівна

Пов’язані теми

Алгебра, 9 клас, Розробки уроків

До підручника

Алгебра 9 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)

До уроку

§ 2. Квадратична функція

Додано

26 жовтня 2021

Переглядів

1093

Оцінка розробки

Відгуки відсутні