Конспект уроку "Множини. Операції над множинами. Множина дійсних чисел."

УРОК 2

Тема уроку: Множини. Операції над множинами. Множина дійсних чисел.

Мета: навчальна: узагальнити та систематизувати знання учнів про степеневу функцію;

розвиваюча: розвивати логічне мислення, увагу;

виховна: виховувати активність, самосвідомість.

Тип уроку: застосування знань та вмінь.

Хід уроку

     I.Організаційний етап

Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.

    II. Перевірка домашнього завдання

Перевірити наявність виконаного домашнього завдання та відповісти на запитання, які виникли в учнів під час його виконання.

    IІІ.Вивчення нового матеріалу

Одним з основних понять, які використовують у математиці, є поняття множини. Для нього не дають означення. Можна пояснити, що множиною називають довільну сукупність об’єктів, а самі об’єкти — елементами даної множини. Так, можна говорити про множину учнів у класі (елементи — учні), множину днів тижня (елементи — дні тижня), множину натуральних дільників числа 6 (елементи — числа 1, 2, 3, 6) тощо. У курсах алгебри та алгебри і початків аналізу найчастіше розглядають множини, елементами яких є числа, і тому їх називають числовими множинами.

Можна розглядати також множину, яка не містить жодного елемента, — порожню множину.

Множини бувають скінченні і нескінченні залежно від того, яку кількість елементів вони містять. Так, множини А = {7}; M = {1; 2; 3} — скінченні, бо містять скінченне число елементів, а множи- ни N, Z, Q, R — нескінченні.

         Дві множини називаються рівними, якщо кожний елемент першої множини є елементом другої множини і, навпаки, кожний елемент другої множини є елементом першої множини.

          Якщо кожен елемент однієї множини A є елементом другої множини B, то кажуть, що перша множина A є підмножиною другої множини B, і записують так: A ⊂ B. Наприклад, {1; 2} ⊂ {0; 1; 2; 3}, N ⊂ Z (оскільки будь-яке натуральне число — ціле), Z ⊂ Q (оскільки будь-яке ціле чис- ло — раціональне), Q ⊂ R (оскільки будь-яке раціональне число — дійсне). Вважають, що завжди ∅ ⊂ A, тобто порожня множина є підмножи- ною будь-якої непорожньої множини.

Операції над множинами

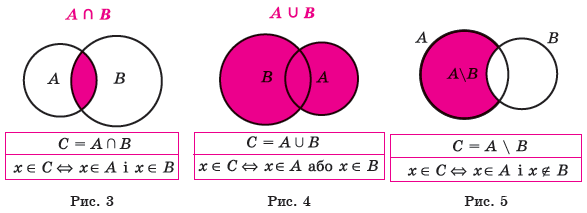
      Перерізом множин А і В називають їхню спільну частину, тобто множину C усіх еле- ментів, що належать як множині А, так і множині В. Переріз множин позначають знаком З (на рисунку 3 наведено ілюстрацію означення перерізу множин). Наприклад, якщо A = {2; 3; 4}, B = {0; 2; 4; 6}, то A Ç B = {2; 4}.

     Об’єднанням множин А і В називають множину С, складену з усіх елементів, що належать хоча б одній із цих множин (А або В). Об’єднання множин позначають знаком И (на рисунку 4 наведено ілюстрацію означення об’єднання множин). Наприклад, для множин A і B з попереднього прикладу A È B = {0; 2; 3; 4; 6}. Якщо позначити множину ірраціональних чисел через M, то M È Q = R.

    Різницею множин А і В називається множина С, яка складається з усіх елементів, які належать множині А і не належать мно жині В. Різницю множин позначають знаком \ (на рисунку 5 наведено ілю- страцію означення різниці множин).

    ІV. Розв’язування вправ

Ст________Впр________________________________________________

1°. Запишіть за допомогою фігурних дужок множину: 1) букв у слові «алгебра»; 2) парних однозначних натуральних чи- сел; 3) непарних однозначних натуральних чисел; 4) однозначних простих чисел.

2°. За якою характеристичною властивістю записано такі множини: 1) {понеділок, вівторок, середа, четвер, п’ятниця, субота, неділя}; 2) {січень, лютий, березень, квітень, травень, червень, липень, сер- пень, вересень, жовтень, листопад, грудень}; 3) {Австралія, Азія, Америка, Антарктида, Африка, Європа}; 4) {до, ре, мі, фа, соль, ля, сі}; 5) {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}?

3°. Наведіть приклади порожніх множин.

    V. Підведення підсумків уроку 

     Наведіть приклади множин, укажіть декілька елементів кожної множини. 2. Як позначають порожню множину, множини натуральних, цілих, раціональних, дійсних чисел? 3. Дайте означення рівності множин. Наведіть приклади двох рівних множин. 4. Дайте означення підмножини. Наведіть приклади. Проілюструйте це поняття за допомогою кругів Ейлера—Венна.

    VІ. Домашнє завдання 

Ст________Впр________________________________________________

Вивчити означення.