Конспект уроку на тему: Формули скороченого множення
Тема уроку: Формули скороченого множення
Мета уроку: Узагальнити і систематизувати знання, вміння та навички у застосуванні формул квадрата двочлена і різниці квадратів. Розвивати вміння узагальнювати, робити висновки. Сприяти розвитку логічного мислення, математичної мови.
Хід уроку
І. Організаційна частина
Привітання
З гарним настроєм хто прийшов – махніть рукою,
Хто чує мене – кивніть головою,
Хто бачить мене-прошу оком моргнути,
Хто любить дітей-ті підводяться тихо,
Хто найвеселіший-ви всім усміхніться.
Хто ввічливий-сусідові злегка вклоніться
ІІ. Перевірка домашнього завдання
Гра «Знайди помилки»
І. 1) (х+3)2=х2+6х+9; ІІ. 1) (m-5)2=m2-10m+25;
(a2-c)2=a4-2a2c-c2; (x2-z)2=x4-2x2z+z2;
2) (ax+b2)2=a2x2+2axb2+b4; 2) (cx+2b)2=c2x2+4cxb+9b2;
(-1+2c3)2=4c6+4c3+1; (-2+3c)2=9c2-12c+4;
3) 12ab-(2a+3b)2=12ab-4a2- 3) 30xc-(3x+5c)2=30xc-9x2-
-12ab-9b2= -4a2-9b2; -30xc-25c2= -9x2-25c2;
4) (х-3)2 =(х-5)(х+4); 4) (х-2)2=(х+3)(х-4);
х2-6х+9=х2+4х-7х-20; х2-4х+4=х2-4х+3х-12;
-6х-4х+5х= -20-9; -4х+4х-3х= -12-4;
-5х= -29; -3х= -16;
х= 5,8. х= 5![]() .
.
ІІІ. Мотивація навчальної діяльності
Вправа «Чарівний глечик»
Пропоную вам дістати по одному папірцю з чарівної коробочки,яка підкаже, що на вас чекає сьогодні або що вам потрібно зробити найближчим часом. Ці побажання чарівно впливають на настрій, підбадьорюють, надають упевненості.
- Тобі сьогодні особливо пощастить!
- Життя готує тобі приємний сюрприз!
- Усе складається для тебе найкращим чином!
- Сьогодні твій день, щасти тобі!
- Сьогодні Фортуна з тобою разом!
- Пам’ятай: ти народилася, щоб бути щасливою!
- Люби себе такою, якою ти є, — неповторною!
- Потурбуйся про здоров’я свого тіла!
- Зроби собі подарунок, ти на нього заслуговуєш!
- Вищі сили оберігають тебе!
- У тебе є все, щоб насолоджуватися життям!
- Усе, що потрібно тобі, легко приходить до тебе!
- Усі твої бажання та мрії реалізуються, повір у це!
- Сьогодні з тобою спокій і радість!
- Сьогодні щасливий день
Ми починаємо урок, а на уроці ми…
Уважні!
Розумні!
Організовані!
Кмітливі!
ІV Актуалізація опорних знань, вмінь, навичок.
1)Пригадайте формули скороченого множення.
2) Але ось біда, до нас потрапили комп’ютерні віруси та наробили багато шкоди.
- перший вірус змішав ліву і праву частини виразів. Поставте їх на свої місця.
- другий вірус заховав окремі доданки або їх частини, відновіть їх.
3) Щоб ваш мозок не заіржавів обчисліть, чому дорівнює 1012.
4) Отримавши відповідь, ви відкриєте відповідну комірку
- (x-8)2 = x2-16, 2) (x+7)(x-3)-x2 = 3979,
x2-16x+64 = x2-16, x2-3x+7x-21-x2 = 3979,
-16x = -16-64, -3x+7x = 3979+21,
-16x = -80, 4x = 4000,
х = 5. x =1000.
3) 4y2-(2y+5)2=-385, 4) (a+5)(a-1)-a2+4a=315,
4y2-4y2-20y-25=-385, a2-a+5a-5-a2+4a=315,
-20y= -385+25, 8a=315+5,
-20y= -360, 8a=320,
y=18. a=40.
5) (x-9)(x+9)-(x-3)2=30, 6) Як називається сума кількох
x2-81-x2+6x-9=30, одночленів? (Многочлен)
6x=30+81+9,
6x=120,
x=20.
І так, ми отримали ЕВКЛІД. Це хто? Послухаємо доповідь учнів.
Геометрична інтерпретація
Фізкультхвилинка
«Цифри»
Хід вправи: стоячи, за інструкціями вчителя виконуємо вправу: «Зараз ми будемо писати цифри у незвичний спосіб.
Цифру 1 «пишемо» носом (кажемо і виконуємо),
цифру 2 – підборіддям,
цифру 3 – правим плечем,
цифру 4 – лівим плечем,
цифру 5 – «пишемо» правим ліктем,
цифру 6 – лівим ліктем,
цифру 7 – правим коліном,
цифру 8 – лівим коліном,
цифру 9 – правою ногою
Ще Евклід знав прийом піднесення до квадрату суми двох доданків, який і ми сьогодні з вами вивчаємо. Правда трактував він це з геометричної точки зору.
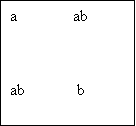
![]() a b
a b
a (a+b)2=a2+2ab+b2.
![]()
b
Але чому тільки квадрат двох чисел? І чому тільки до квадрату? А чи не можна знайти метод піднесення до третього , четвертого і більш високих степенів суми трьох, чотирьох і більше доданків? Давайте спробуємо. В зошитах накресліть квадрат і спробуйте записати формулу квадрата суми трьох чисел.

![]()
![]() а b c
а b c
![]() а
а
![]() b c (a+b+c)2=a2+b2+c2+2ab+2ac+2bc.
b c (a+b+c)2=a2+b2+c2+2ab+2ac+2bc.
А давайте виведемо цю формулу з точки зору алгебри, кажуть, аналітично: (a+b+c)2=(a+b+c)(a+b+c)=a2+ab+ac+ab+b2+bc+ac+bc+c2= =a2+b2+c2+2ab+2ac+2cb.
Отже, квадрат тричлена дорівнює сумі квадратів всіх виразів і подвоєних добутків всіх можливих пар цих виразів.
Спробуйте дописати наступні рядки і виправити формулу четвертого степеня двочлена:
(a+b)4 =a4+4a3b+6a2b2+4ab3+b4.
Піднесіть двочлен до п’ятого степеня, використовуючи вказані властивості:
(a+b)5 =a5+5a4b+10a3b2+10a2b3+5ab4+b5.
Додаткове завдання.
V. Домашнє завдання.
Математичне кафе – кожен обирає собі додаткове завдання на певну оцінку
VІ. Підведемо підсумок сьогоднішнього уроку.
Ідентифікація ( перед учнями фарба, вкінці уроку вони визначають чи сподобався урок, якщо так – червона фарба, ні – зелена)
![]()


про публікацію авторської розробки
Додати розробку
