Бінарний урок з алгебри та інформатики на тему "Найпростіші перетворення графіків функцій"

Бінарний урок з алгебри у 9 класі.

Тема уроку. Найпростіші перетворення графіків функцій

Мета уроку: - сформувати розуміння учнями змісту поняття «перетво­рення графіка функції», а також розуміння того факту, що певне перетворення рівняння функції тягне за собою перетворення графіка та навпаки. Сформувати знання учнів про основні види геометричних перетворень графіків функцій (на інтуїтивному рівні) та про рівняння функції, що задається цим перетворенням. Сформувати первинні уміння «читати» графіки функцій (тобто за готовими графіками задавати рівняння функцій), а також виконува­ти побудови графіків функцій за допомогою перетворень, заданих рівнянням даної функції.

- продемонструвати можливість та доцільність використання комп’ютерної програми “ Geo Gebra ” при вивченні даної теми;

- розвивати уяву, логічне мислення, спостережливість, вміння аналізувати; виховувати охайність математичних записів та малюнків.

Епіграф

Немає людини, яка б не робила помилок, але той, хто виправляє свої помилки - мудрець.

         Китайський вислів 

Хід уроку

I. Організаційний етап. Повідомлення  теми  й мети  уроку.

Вчитель інформатики:

Повторюються правила техніки безпеки в комп’ютерному класі.

II. Перевірка домашнього завдання. Актуалізація опорних знань

1.Робота в парах (Лото)

Учні отримують конверти з картками, на яких схематично зображені графіки функцій та окремо – функції, задані формулами. Учні, працюючи в парах, співставляють зображення графіка функції та її аналітичним записом.

2. Усні вправи

1. Залежність, при якій кожному значенню аргументу відповідає одне єдине значення у, називається …

2.Назвіть способи задання функції.

3. Усі значення, які набуває незалежна змінна, називаються областю …

4. Усі значення, які набуває залежна змінна, називаються областю …

5. Для побудови прямої, яка є графіком лінійної функції, потрібно … точки.

 

 

III. Формулювання мети і завдань уроку.
Мотивація навчальної діяльності учнів. Постановка проблемного питання.

На дошці записано функції:

;  ;   ;  ; ;    ;   .

1. Графік якої з наведених функцій ви побудували б якнайшвидше?

2. А який би з цих графіків вам не хотілося б будувати самостійно?

3. Який спосіб побудови графіків функцій ви найчастіше застосовували на уроках? (Варіант відповіді: складання таблиці значень аргументу та функції, побудова графіка за координатами точок)

4. Скільки часу забирає такий спосіб побудови графіків функцій?

– Дійсно, для дослідження функції та побудови її графіка потрібно багато часу, доводиться виконувати багато громіздких обчислень. Це незручно.

– Сьогодні на уроці ми розглянемо з вами ще один спосіб побудови графіків функцій за допомогою так званих геометричних перетворень. Крім того, познайомимось з програмним засобом GeoGebra

Вчитель інформатики:

На уроці інформатики ми з вами вивчали історію розвитку обчислювальної техніки. Давайте пригадаємо коли і ким була винайдена перша машина, що виконувала чотири арифметичні дії?

Доповідь учня:

Перша машина, що дозволяє легко виконувати  віднімання, множення і ділення, була винайдена в Германії Готфрідом Вільгельмом Лейбніцем. У 1672 році, знаходячись в Парижі, Лейбніц познайомився з голландським математиком і астрономом Хрістіаном Гюйгенсом. Бачивши, як багато обчислень доводиться робити астрономові, Лейбніц вирішив винайти механічний пристрій для розрахунків. У 1694 році він завершив створення механічного калькулятора.

ІV. Вивчення нового матеріалу

Вчитель інформатики

На сьогодні розроблено значну кількість програмних засобів, що дозволяють розв’язувати досить широке коло математичних задач за допомогою комп’ютерів. Це прикладні програми навчального призначення. Сьогодні на уроці ми скористаємося однією з таких програм, яка дуже спрощує процес побудови графіків функцій. Звернемось до програми GeoGebra, оскільки  Лейбніц говорив, що «Негідно обдарованій людині, витрачати подібно рабу, час на обчислення, які, безумовно, можна було б довірити будь-якій особі, якщо при цьому застосувати машину»

Для того, щоб побудувати  графік в програмі GeoGebra необхідно:

Інструкційна карта

•  У рядок <Введення> ввести формулу функції і натиснути клавішу <Enter>.

•  Треба пам’ятати: множення - *, ділення - /, степінь - ^, модуль – abs(), квадратний корінь – sqrt().

•  На полотні графічних побудов отримаємо графік шуканої функції, а на панелі об’єктів його аналітичне представлення.

•  Навівши покажчик миші на графік функції, клацнути правою кнопкою миші і в контекстному меню обрати пункт Властивості.

•  За допомогою діалогового вікна, що з’явиться, скориставшись вкладкою <Основні> і оберіть в контекстному меню «Показувати значення»  значення «Ім’я і значення»

Програма GeoGebra  може працювати в режимі електронної таблиці, тому потрібно пам’ятати, що формула електронної таблиці починається зі знака =, може містити знаки арифметичних операцій, адреси клітинок, числа, функції             

 

Робота в групах (дослідження)

Клас об’єднується у чотири групи. Кожна група отримує завдання для досліджень.

Завдання для І групи:

1. Побудувати в одній координатній площині графіки пар функцій:

 

а) y = 2x² , y = –2x²;           б) ;  

2. Схематично зобразити на аркуші отримані графіки функцій (кожна пара графіків зображується окремо).

3. Дослідити закономірність у правилах побудови графіків.

4. Знайти у підручнику правило, що описує дану закономірність (правило записане на сторінці 92).

Завдання для ІІ групи:

1. Побудувати в одній координатній площині графіки трійок функцій:

а) ;   ;                            б) ;    ;          

2. Схематично зобразити на аркуші отримані графіки функцій (кожна пара графіків зображується окремо).

3. Дослідити закономірність у правилах побудови графіків.

4. Знайти у підручнику правило, що описує дану закономірність.

Завдання для ІІІ групи:

1. Побудувати в одній координатній площині графіки трійок функцій:

а) ;      ;                     б) ;     ;    

2. Схематично зобразити на аркуші отримані графіки функцій (кожна трійка графіків – окремо).

3. Дослідити закономірність у правилах побудови графіків.

4. Знайти у підручнику правило, що описує дану закономірність (с. 93-94).

Завдання для ІV групи:

1. Побудувати в одній координатній площині графіки трійок функцій:

а) ;     ;                            б)  ;  ; 

2. Схематично зобразити на аркуші отримані графіки функцій (кожна трійка графіків – окремо).

3. Дослідити закономірність у правилах побудови графіків.

4. Знайти у підручнику правило, що описує дану закономірність (правило записане на сторінці 94).

Звіт груп

 

Узагальнення вмінь

Фронтальна робота

Письмові вправи

Побудуйте графіки функцій

1) у=х²-3;  

2)

3) у=(х-1)²;

4) у=(х-1)²-1.

Індивідуальні завдання для роботи за комп’ютером

1. Скориставшись програмою “ GeoGebra ” визначіть функцію, графік якої отримаємо після наступних перетворень графіка функції у=х²

а) паралельного перенесення графіка  на 2 одиниці ліворуч і на 3 одиниці вгору.

б) паралельного перенесення графіка  на 3 одиниці вниз і на 4 одиниці праворуч

2. Скориставшись програмою “ GeoGebra ” визначіть функцію, графік якої отримаємо після наступних перетворень графіка функції у=х²

а) паралельного перенесення графіка  на 4 одиниці ліворуч і на 2 одиниці вниз.

б) паралельного перенесення графіка  на 3 одиниці вгору і на 4 одиниці праворуч

3. Скориставшись програмою “ GeoGebra ” визначіть функцію, графік якої отримаємо після наступних перетворень графіка функції у=х²

а) паралельного перенесення графіка  на 2 одиниці праворуч і на 4 одиниці вгору.

б) паралельного перенесення графіка  на 2 одиниці вниз і на 4 одиниці ліворуч

4. Скориставшись програмою “ GeoGebra ” визначіть функцію, графік якої отримаємо після наступних перетворень графіка функції у=х²

а) паралельного перенесення графіка  на 3 одиниці праворуч і на 2 одиниці вгору.

б) паралельного перенесення графіка  на 4 одиниці вниз і на 2 одиниці ліворуч

 

 

Додатково 

1. Побудувати графік функції y=(x+3)²-1. Користуючись графіком функції,   знайти:

 а) область значень функцій;

 б) значення х, при яких функція приймає від’ємні значення;

 в) проміжки, на яких функція спадає.

2.Побудувати графіки функцій за допомогою перетворень графіків функцій у=х², у=х³

а) у=(х-3)(х+3)                 б) у=(х-1)³                   в) у=(х+1)²-2х                   г) у=(х-2)²-3               

3.Розв’язати  графічно рівняння:  (х-2)²=4-х

VI. Підсумки уроку

Сьогодні на уроці ви вивчали найпростіші перетворення графіків функцій з алгебри, навчались будувати графіки в програмі GeoGebra.

 Визначте, який вигляд мають функції, графік яких утворю­ється з графіка функції y = g(x) шляхом виконання:

1. паралельного перенесення графіка y = g(x) на 2 одиниці ліворуч;
2. паралельного перенесення графіка y = g(x) на 2 одиниці вниз;
3. симетрії графіка y = g(x) відносно осі абсцис;
4. розтягнення графіка y = g(x) у 2 рази вздовж осі ординат;
5. стиснення графіка y = g(x) у 2 рази вздовж осі абсцис.

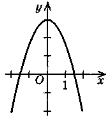
Графік якої функції зображений на рисунку? 1) у = х2 + 3;                  2) у = х2 – 3; 3) у = -х2 + 3;                 4) у = -х2 – 3.

VII. Домашнє завдання §10 повторити § 8, 9  №411 (а); №414; №415