Конспект уроку на тему "Функція y = √x та її графік. Степінь з раціональним показником та її властивості."

Тема. Функція y  ⁿ x та її графік. Степінь з раціональним показником та її властивості.

Мета: сформувати в учнів розуміння змісту поняття функції y  ⁿ x ; сформувати вміння знаходити область визначення та множину значень цієї функції; досліджувати функцію y  ⁿ x на парність та непарність; визначити проміжки зростання та спадання функції; будувати її графік.

Тип уроку: засвоєння знань, формування вмінь.

Література:

- Для вчителя:

1.     Бевз Г.П. Алгебра: підручник для кл. з поглиб. вивч. матем 10 кл. – К.:

Генеза, 2010. – 342 с.

2.     Математика. Комплексне видання: Довідник з математики. 5 – 11 класи. Аналіз найпоширеніших помилок. Тестові завдання/ О.С. Будна, С.М. Будна, А.Р. Гальперіна, М.Я. Забєлишенська, О.Я Михеєва. – Х.:

«Літера» ЛТД, 2009. – 320 с.

- Для учнів:

1. Бевз Г.П. Алгебра: підручник для кл. з поглиб. вивч. матем 10 кл. – К.:

Генеза, 2010. – 342 с.

Структура уроку

I.                                  Організаційний етап                                                                              (1 хв.)

II.                               Перевірка домашнього завдання                                                           (5хв.)

III.                            Актуалізація опорних знань                                                        (5хв.)

IV.                           Вивчення нового матеріалу                                                         (10хв.)

V.                              Засвоєння вмінь та навичок                                                        (20хв.)

VI.                           Підбиття підсумків уроку                                                                     (2хв.)

VII.                        Домашнє завдання                                                                       (2хв.)

Хід уроку.

I.                   Організаційний етап.

Перевірка готовності учнів до уроку, налаштування на роботу.

II.                Перевірка домашнього завдання.

III.            Актуалізація опорних знань.

Фронтальне опитування:

1.     При яких значеннях x має зміст вираз:

а) ⁿ x 3 ; б) ⁴ 72x ; в) ¹⁰  x

2.     Сформулюйте означення парної та непарної функції. Дослідіть на парність функції:

а) f (x)  2x³; б) f (x)  3x⁴; в) f (x)  x 1;

3.     Як розміщенні графіки парної та непарної функції?

4.     Яка функція називається зростаючою? Спадною? Наведіть приклади.

5.     Які елементарні перетворення графіків функції ви знаєте? Як можна побудувати графік функції:

а) f (x)  (x 4)³; б) f (x)  x⁴ 4; в) f (x) x5 ; Г) f (x) x 5;

IV.             Засвоєння знань.

План.

1. 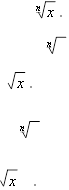                Означення функції y 

2.                 Властивості функції y  x .

3.                 Графік функції y  ⁿ

Функція вигляду y  x , де nN,n 2 називається функцією y  ⁿ x .

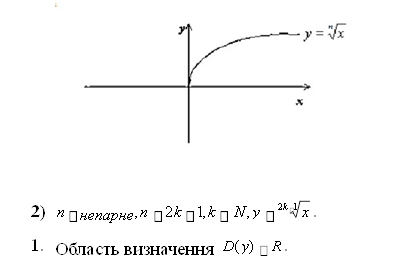
1) nпарне,n  2k,k N, y  ^2k

1.     Область визначення 0;.

2.     Множина значень 0;.

3.     Парність, непарність – ні парна, ні непарна.

4.     Зростання, спадання – зростає при x0;.

5.     Графік функції.

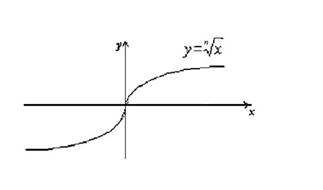
2.     Множина значень E(y) R.

3.     Парність, непарність – непарна.

4.     Зростання, спадання – зростає при xR.

5.     Графік функції.

 

Степенем додатного числа a з раціональним показником r , поданим у вигляді m , де mZ,nN,n1, називається число n am , тобто ar amn  n am . n

Наприклад, 5  ⁷ 5³ ,3^  ³ 3^1 ,_0,4^0,3  0,4 ¹⁰ 0,4³ .

Властивості степеня з раціональним показником:

Для будь-яких a0 і b0 і будь-яких раціональних p і q виконується:

1)ap aq  apq 2)ap  aq  apq

3)(a^p)^q  a^pq            4)(ab)^p  a^pb^q

^ a p ap

        5) b   b_p



V.   Формування вмінь.

1.     Знайдіть область визначення функції:

a)   f (x) 

b) 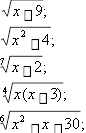  f (x)  ³

c)    f (x) 

d)   f (x) 

e)    f (x) 

2.     Укажіть множину значень функції:

a)   f (x)  ⁵ x 3;

 

b)   f (x)  ⁶ x 3;

3.     Дослідіть на парність функції:

a)   f (x)  ²⁰ x;

 

b)   f (x)  ²¹ x;

4.     Укажіть множину, на якій зростає функція:

a)   f (x)  ¹⁰ x;

 

b)   f (x)  ¹³ x  2;

5.     Чи належить графіку функції y  ³ x7 точка:

a)   A(34;3);

b)   B(1;2);

c)    C(0;7);

6.     Не розв’язуючи рівняння, визначте, чи може число -1 бути розв’язком рівняння ²⁶ x(x3) 3.

7.     Побудуйте графік функції:

a)      y  ⁴ x 1;

b)      y  ³ x  2;

c)       y  ⁵ x 1;

8.     Подайте степінь з дробовим показником у вигляді кореня:

a)      5 ;       e)(ab);

b)      a ;                                    f )ab; 

            c)b;                                      g)(m  n)2,5 ;

1

1

            d)10^_;                                     h)(x 3y) ³ ;

9.     Подайте корінь у вигляді степеня з дробовим показником:

a)      x;         e)⁴ a³;

b)      5 22 ;   f )1149;

              

c)       ⁷ 6⁵ ;     g)⁸ (a b)⁷ ;

d)      ³ 3a;     h)⁸ a⁷ b⁷ ;

10.Знайдіть значення виразу:



             a)4;                                         e)0,216;

           b)25;                                 f )33 ;

                                                                 8



c)364;

g)27;



             d) 50,01^;                           h)320,2 ;

11.Спростіть вираз:

1     2 a 6 a 3

                   1           1                                                                  e⁾        ₁        ;

            a)a2 a3;                                       a4

            b)(a² )³;                                   f )(a ⁶ b ²⁷ ) ⁴ ;

                

                                                                                      5            1



               c)a a;                                     a ² b¹²

                                                                           g)     17            1 ;



             d)a2 a6 a3;                             a 4 b 3

h)(a)1,8 (a)2,4 ;

VI.                Підсумки уроку.

1.     Що називається Функцією y  ⁿ x ?

2.     Які ви знаєте властивості функції y  ⁿ x коли:

          а)        nпарне;

          б)        nнепарне;

3.     Що називається степенем додатного числа з раціональним показником?

4.     Які ви знаєте властивості степеня з раціональним показником?

VII.            Домашнє завдання.

Вивчити теоретичний матеріал, з підручника «Бевз Г.П. Алгебра 10клас» №:

1.     543(1,2);

2.     544(1);

3.     545;

4.     549.