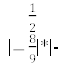Конспект уроку на тему: "Модуль числа"
Урок 81 Дата 18.02.2021
Тема уроку: модуль числа.
Мета уроку:
а) навчальна: сформувати в учнів уявлення про геометричний зміст поняття «модуль числа»; виробити вміння читати, записувати вирази, що містять модуль, а також знаходити значення виразів, що містять числа під знаком модуля; навчити розв’язувати рівняння, що передбачають застосування поняття «модуль числа»;
б) виховна: виховувати працьовитість, старанність, кмітливість,
доброзичливість та любов до математики;
в) розвивальна: розвивати систематичність, послідовність мислення, культуру математичної мови і записів; сприяти розвитку уяви, творчої активності учнів, а також пам’яті, уваги, логічного мислення.
Тип уроку: комбінований (урок вивчення нових знань та засвоєння навичок і умінь)
СТРУКТУРА УРОКУ
1. Перевірка виконання домашнього завдання, актуалізація попередніх знань учнів та їх корекція.
2. Повідомлення теми, мети, задач уроку та мотивація учбової діяльності.
3. Сприйняття та первинне усвідомлення нового матеріалу.
4. Первинне застосування набутих знань (пробні вправи).
5. Застосування учнями знань та вмінь в стандартних умовах із метою набуття навичок (тренувальні вправи).
6. Підсумки уроку. Домашнє завдання.
Обладнання уроку: підручник, дидактичні матеріали.
|
Етап уроку |
Діяльність вчителя |
Діяльність учнів |
Примі тки |
|
|
Вітання з класом. Перевірка домашнього завдання.
Фронтальне опитування
1. Яку пряму називають координатною?
2. Яке число відповідає точці початку відліку на координатній прямій? 3. Які числа називають додатніми?
4. Які числа називають від’ємними?
5. Як позначаються додатні числа? (яким знаком) 6. Як позначаються від’ємні числа? (яким знаком) 7. Нуль – це додатне число чи від’ємне?
А чи знаєте ви в якому місті європейської країни стоїть пам’ятник нулю? Давайте дізнаємося про це місто, позначивши подані точки на координатній прямій: П(3), А(-2), Ш(7), Б(-8), Т(9), Д(-4), У(-6), Е(5). |
Учні вітаються з вчителем.
Учні дають відповіді на запитання. 1. Пряма, на якій позначено початок відліку, одиничний відрізок і напрямок, називається координатною прямою. 2. Число «нуль».
3. Числа, які знаходяться праворуч від точки відліку на координатній прямій. 4. Числа, які знаходяться ліворуч від точки відліку на координатній прямій. 5. Знаком «+», або ніяким знаком. 6. Знаком «-».
7. Нуль – не додатнє, не від’ємне.
|
|
|
|
Тема сьогоднішнього уроку «Модуль числа». Щоб краще зрозуміти цю тему давайте виконаємо наступне завдання.
Якось запросила Баба Яга Лісовика прогулятися в її лісі. Для того, щоб гість орієнтувався на місцевості накреслила Баба Яга схему-підказку у вигляді координатної прямої, де одиничним відрізком був один крок змія Горинича. Повісила свою підказку на старий дуб. Але дощ змив чорнило. Відновіть рукопис - напишіть місце розташування основних пунктів казкового лісу. Алгоритм виконання завдання: 1. Який об’єкт стане точкою відліку? 2. Визначити координати інших об’єктів відносно точки початку відліку 3. Заповніть таблицю:
- Чим відрізняються координати об’єктів від їх відстані до точки початку відліку? |
Діти уважно слухають розповідь вчителя.
1. Дуб 2. Дуб (0), Курочка ряба (4), Хатинка на курячих ніжках (8), Вчений кіт (-4), Соловейрозбійник (-10) 3. Заповнення таблиці.
Учні висловлюють свою думку. |
|
|
|
- Порівнюючи відстані від даних об’єктів до Дуба, ми шукали довжини відповідних відрізків. Кажуть: ми шукали модуль кожного із чисел -4, 4, -10, 8. Отже, модуль числа -10 дорівнює 10, а модуль числа -4, так само, як і модуль числа 4, дорівнює 4. - Модуль числа позначають двома вертикальними рисками: ||. Запис |а| читають: «Модуль числа а». Для чисел -4, -10, 8, 4 можемо записати: |-4|=4, |-10|=10, |4|=4, |8|=8. - Модуль числа показує, на якій відстані від початку відліку знаходиться дане число на координатній прямій. - Як ви гадаєте чи можна сказати модуль числа дорівнює -24. - Так, правильно. Дана фраза не має змісту. А чому дорівнює модуль числа 0? Модуль числа 0 дорівнює нулю: |0|=0. - Давайте зберемо всі властивості модуля числа докупи. Властивості модуля числа 1. Модуль додатного числа дорівнює самому числу. 2. Модуль від’ємного числа дорівнює протилежному числу. 3. Модуль числа 0 дорівнює нулю. |
Учні слухають пояснення вчителя.
4. Ні, оскільки відстань не може дорівнювати від’ємному числу.
|
|
|
|
№983 (усно) На якій від початку відліку розміщується кожна точка (мал. 110)? Чому дорівнює модуль її координати?
№984 (усно) Чи може модуль числа дорівнювати: 1) 0; 2) -2; 3) 4) 6) ; 7) ; 8) −101,1?
|
|
№983 А(2), В(5); F(7); C(-2); D(- 5). |2|=2; |5|=5; |7|=7; |-2|=2; |-5|=5.
№984 1) так; 2) ні; 3) так; 4) так; 5) ні; 6) ні; 7) так; 8) ні. |
|
|
|
№1004 Якими даними заповнити таблицю 7? 1) 13; 2) -6; 3) 5,7; 4) 0; 5) 6) ; 7) ; 8) 9)
№1006 Обчисліть: 1) |-3|*|-4|; 2) 3) |0|*|-5|; 4) 5) 9|; 6) |144|:|-12|. |
треба |
№1004 1) 13; 2) 6; 3) 5,7; 4) 0; 5) 6) ; 7) ; 8) 9) 10) 700.
№1006 1) 3*4=12; 2) 4) ; 5) ; 6) 144:12=12.
|
|
|
|
№ 1014 Знайдіть число, протилежне до значення суми: 1) |15|+|38|; 2) |-16|+|11|; 3) |43|+|-28|; 4) |-101|+|-6|.
№1011 Розв’яжіть рівняння 1) |x|=15; 2) |x|=100; 3) |x|=4,5; 4) 5) ; 6) |x|=0; 7) |x|=-3. |
№1014 1) 15+38=53; 2) 16+11=27; 3) 43+28=71; 4) 101+6=107.
№1011 1) x=±15; 2) x=±100; 3) x=±4,5; 4) 5) ; 6) x=0; 7) немає розв’язків. |
|
|
|
|
- Що ми вивчили сьогодні на уроці? - Що таке модуль?
- Модуль від’ємного числа дорівнює … . - Модуль додатного числа дорівнює … . - Модуль нуля дорівнює … .
Повідомлення завдання додому: №1005, №1015, №1012. |
- Модуль числа. - Модуль числа показує, на якій відстані від початку відліку знаходиться дане число на координатній прямій. - Протилежному йому числу.
- Цьому ж самому числу.
- Нулю.
Діти записують завдання в щоденник. |
|
|
Розв’язання домашнього завдання


про публікацію авторської розробки
Додати розробку


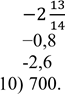 -8,7;
-8,7;