Конспект уроку на тему "Подільність націло та її властивості"
Цикл уроків з теми «Основи теорії подільності» стане у нагоді вчителям, що працюють у класах з поглибленим вивченням математикиє. І хоча дана тема не є простою, але вона одна з тих, де найбільш яскраво проявляється здатність учнів до евристичного мислення. Усім урокам характерне використання різноманітних форм роботи на різних етапах засвоєння знань. Деякі уроки доповнені презентаціями, це допоможе вчителю зробити уроки цікавими і доступними для учнів.
- 1.ppt ppt
- 2.ppt ppt
- 1 подільність націло та її властивості .doc doc
Цикл уроків з алгебри на тему «Основи теорії подільності»
для 8 класів з поглибленим вивченням математики
Урок №1 Тема: Подільність націло та її властивості
Мета: Навчити учнів доводити подільність цілих чисел, розв’язувати рівняння з двома змінними в цілих числах; розвивати розумові операції, вміння аналізувати, порівнювати, узагальнювати, класифікувати, розмірковувати за аналогією; розвивати творче мислення; виховувати волю і мотиви діяльності.
Тип уроку: комбінований урок
Обладнання: підручник, презентація1, презентація 2
Хід уроку:
- Мотивація навчання
- Як ви вважаєте, що вивчає теорія подільності чисел? Яке її основне завдання? Які властивості подільності ви пам’ятаєте з молодших класів?
- Під час вивчення основ теорії подільності ми навчимося доводити подільність цілих чисел, розв’язувати рівняння з двома змінними в цілих числах, ознайомимось з такими поняттями, як конгруенція, а також з рядом теорем, що пов’язані з подільністю чисел. (Презентація 1)
- Пояснення нового матеріалу (Презентація 2)
Означення: Кажуть, що ціле число а ділиться націло на ціле число b, ![]() , якщо існує таке ціле число k, що
, якщо існує таке ціле число k, що ![]() .
.
-
Якщо а ділиться на b, то пишуть:
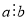 , наприклад,
, наприклад, 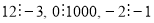 .
.
-
Якщо
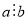 , то число b називають дільником числа а, а число а – кратним числа b. Також кажуть, що число а кратне числу b
, то число b називають дільником числа а, а число а – кратним числа b. Також кажуть, що число а кратне числу b
- Розглянемо основні властивості подільності націло
-
Якщо
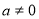 , то
, то 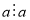 .
.
-
Якщо
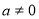 , то
, то 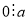 .
.
-
Якщо
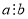 , то
, то 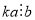 .
.
-
Якщо
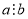 і
і 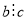 , то
, то 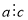 .
.
-
Якщо
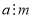 і
і 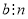 , то
, то 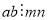 . 6) Якщо
. 6) Якщо 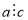 і
і 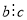 , то
, то 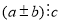
Розв´язування вправ
- Усне розв’язання вправ («Математичний футбол»)
1. Чи дiлиться число a на -a? Чи дiлиться число -a на a?
2. В якому випадку два цiлих числа a i b мають таку властивiсть, що a дiлиться на b i b дiлиться на a?
3. Числа a i b такi, що 0 < a < b. Чи може a дiлитися на b?
4. Доведiть, що добуток трьох послiдовних натуральних чисел дiлиться на 3.
5. Доведiть, що якщо ab + cd дiлиться на ![]() , то ad+bc також дiлиться на a-c.
, то ad+bc також дiлиться на a-c.
6. Доведiть, що число mn (m +n) — парне.
7. Вiдомо, що a кратне 3, b кратне 2. Доведiть, що 2a + 3b кратне 6.
8. Дрiб![]() скоротний. Чи скоротний дрiб
скоротний. Чи скоротний дрiб ![]() ?
?
9. Доведiть, що 13 +23 +33+ ... 993 дiлиться на 100.
10. Доведiть, що будь-яке натуральне число, десятковий запис якого складається iз 3n(n є N) однакових цифр, дiлиться на 37.
11. Доведiть, що:
а) ![]() кратне 9;
кратне 9;
б) ![]() кратне 99;
кратне 99;
в) ![]() дiлиться на 11;
дiлиться на 11;
г) ![]() дiлиться на 11.
дiлиться на 11.
12. Доведiть, що якщо ![]() ціле число, то
ціле число, то ![]() також цiле число.
також цiле число.
13. Доведiть, що якщо в трицифровому числi двi останнi цифри однаковi, а сума його цифр дiлиться на 7, то i саме число дiлиться на 7.
14. Яких чисел бiльше серед першої тисячі натуральних чисел: тих, якi дiляться на 3 або на 5, чи тих, якi не дiляться нi на 3, нi на 5?
15. Чи iснує таке натуральне число n, щоб сума 1+2+3…+n дорiвнювала трицифровому числу, яке складалося б з однакових цифр?
16. Доведiть, що:
a) (a2-b2)![]()
![]()
![]()
![]()
в) (a2-b2)![]()
![]()
![]()
![]()
- Колективне розв’язування «Метод пропозицій»
1) Цілі числа ![]() такі, що
такі, що ![]() . Доведіть, що
. Доведіть, що ![]() .
.
Розв’язання: Маємо: ![]() . Оскільки
. Оскільки ![]() , то за властивістю 6
, то за властивістю 6 ![]() . Тоді з властивості 3 випливає справедливість твердження, що доводиться.
. Тоді з властивості 3 випливає справедливість твердження, що доводиться.
Означення: Розв’язати рівняння з двома змінними в цілих числах означає знайти всі пари цілих чисел, які є розв’язками цього рівняння.
2) Розв’яжіть у цілих числах рівняння ![]() .
.
Розв’язання: Розкладемо ліву частину рівняння на множники: ![]() . Тоді можливі чотири випадки:
. Тоді можливі чотири випадки:
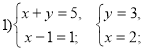
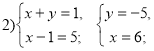
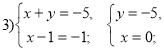
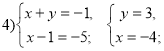
Відповідь: (2;3), (64-5), (0;-5), (-4;3)
3) Цілі числа ![]() такі, що
такі, що ![]() . Доведіть, що
. Доведіть, що ![]() .
.
Розв’язання: Маємо ![]() . Оскільки
. Оскільки ![]() , а з умови і властивості 3 випливає, що
, а з умови і властивості 3 випливає, що ![]() , то за властивістю 6 різниця, що розглядається, кратна 31.
, то за властивістю 6 різниця, що розглядається, кратна 31.
- Домашня робота
-
Число
 кратне 7. Доведіть, що
кратне 7. Доведіть, що  .
.
-
Число
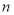 кратне 4. Доведіть, що
кратне 4. Доведіть, що 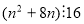
-
Числа
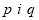 такі, що
такі, що 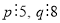 . Доведіть, що
. Доведіть, що 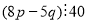
-
Розв’яжіть у цілих числах рівняння: а)
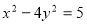 , б)
, б) 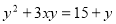
Використані джерела:
1. Алгебра підручник для 8 класу з поглибленим вивченням математики,
А.Г. Мерзляк, В.Б. Полонський, М.С. Якір, - Харків, «Гімназія», - 2009
2. Алгебра та початки аналізу 10 клас, профільний рівень
А.Г. Мерзляк, Д.А. Номіровський, В.Б. Полонський, М.С. Якір, - Харків «Гімназія», - 2010
3. О.Ю. Карік, Матеріали для факультативних занять, спецкурсів, гуртків, математика 5-7, Харків, - «Основа», - 2008


про публікацію авторської розробки
Додати розробку