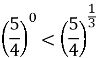Конспект уроку на тему: "Показникова функція"

   Методична мета уроку: застосування інформаційно-комунікативних технологій в процесі формування вмінь та навичок учнів.

УРОК 19

ТЕМА: ПОКАЗНИКОВА ФУНКЦІЯ

МЕТА:

Навчальна: засвоїти означення та властивості показникової функції, розрізняти показникову функцію серед інших елементарних функцій;

Розвиваюча: розвивати вміння аналізувати графіки та властивості показникової функції;

Виховна: виховувати інтерес до вивчення математики через показ, де саме застосовують у житті властивості показникової функції.

Компетенції:

Спілкування державною мовою (уміння ставити запитання і розпізнавати проблему; міркувати, робити висновки на основі інформації, поданої в науковій презентації)

Математична – уміння оперувати  алгебраїчними об’єктами, розрізняти види функцій; застосовувати показникову функцію до опису відношень між об’єктами навколишнього світу.

ТИП УРОКУ: засвоєння нових знань.

ОБЛАДНАННЯ: навчальна презентація, мультимедійне обладнання.

МЕТОД  ПРОВЕДЕННЯ: розповідь, бесіда, розв’язування вправ.

Міжпредметні зв’язки:

    забезпечуючі:    Математика «Степінь з довільним показником та 

                   його властивості», «Графіки функцій та їх властивості»;

    забезпечувані:  Фізика «Фізика атомного ядра», Інформатика «Фінансові розрахунки», Біологія «Молекулярні основи біології» Технологія приготування їжі з основами товарознавства.

 

ХІД УРОКУ:

I. Організаційна частина уроку

• Привітання
• Перевірка присутніх на уроці
• Налаштування на роботу

     (Метод: психолого-педагогічної підтримки роботи учнів на занятті, рефлексія) 2 хв.

Мета етапу: створення сприятливого психологічного клімату на уроці.

 

Слайд 2

Сьогодні  на уроці ми працюватимемо разом, я розраховую на вашу підтримку та допомогу. Кожному з вас я хочу побажати, щоб на цьому уроці ви були:

„У"- усміхненими

„С"- спокійними

„П"- прогресивними

„І"- ініціативними

„X"- хоробрими

Іншими словами, я бажаю вам УСПІХУ!

І не тільки на уроках математики, бо досягнення успішного результату під час розв'язування задач - зовсім не привілей математики. Усе людське життя - це не що інше, як постійне бажання досягти успіху у вирішенні нових питань та проблем.

Підніміть руку, хто бажає досягти успіху? Я теж бажаю досягти  успіху.

ІI. Актуалізація опорних знань.

Мета етапу: організувати цілеспрямовану діяльність учнів:

• розвинути внутрішню мотивацію учнів до теми, що вивчається;
• навчити учнів прогнозувати очікувані результати уроку;
• відтворити необхідні знання та вміння для досягнення результатів уроку.

Слайд 3

1. Вправа «Кошик знань». Я називаю перше слово, а учні «ланцюжком» доповнюють «кошик» основними термінами, поняттями. Наприклад: функція – графік – область визначення функції …

 

Слайд 4

2. Питання на повторення

Методичний прийом «Продовжити речення»

• Числовою функцією називається….

Числовою функцією з областю визначення D називається залежність, при якій кожному числу x із множини D (області визначення) ставиться у відповідність єдине число y.

При цьому х називають аргументом (незалежною змінною), у — функцією (залежною змінною).

 

Слайд 5

• Графіком функції називається…

Графіком функції називається множина всіх точок координатної площини з координатами (x; f(x)), у яких абсциси належать області визначення функції, а ординати дорівнюють відповідним значенням функції.

• Область визначення функції…

Область значень функції f – це множина тих значень, яких може набувати аргумент x. Позначення: D(f)

• Область значень функції…

Область значень функції f – це множина, яка складається із всіх чисел f(x), де x належить області визначення. Її позначають E(f).

• Функція зростаюча, якщо…

Функція f(x) називається зростаючою на множині M, якщо більшому значенню аргументу з цієї множини відповідає більше значення функції.

• Функція спадна, якщо…

Функція f(x) називається спадною на множині M, якщо більшому значенню аргументу з цієї множини відповідає менше значення функції.

 

Слайд 6

3. Усна вправа

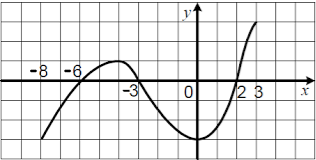1. Використовуючи графік даної функції, назвати:

1) D (f);

2) E (f);

3) нулі функції;

4) проміжки зростання та спадання функції;

5) проміжки знакосталості функції.

 

Слайд 7

Великий Галілео Галілей казав, що природа формулює свої закони мовою математики.

 

Слайд 8

Більшість процесів у житті пов’язано із залежністю між величинами. Наприклад, кількість виконаної роботи залежить від її обсягу та складності самої роботи, вартість покупки від кількості купленого товару і цін. Одна залежність носить випадковий характер, інші постійні. Вони описуються за допомогою функцій.

 

Слайд 9

 

 

Сьогодні ми з Вами розширимо круг функцій, які ви знаєте. Наведіть приклади раніше вивчених функцій.

Відповіді: 1. Лінійна  функція.

                  2. Квадратна функція.

                  3. Тригонометрична функція.

                  4. Степенева функція.

І сьогодні ми з вами розглянемо ще одну функцію яка називається показниковою.  (учні відкривають зошити записують число і тему уроку, план уроку)

 

Ми з'ясували, чого хочемо досягти, але на цьому етапі не менше важливим є питання, нащо нам це потрібно, навіщо вивчається ця тема?

 

Слайд 10

 В природі і техніці часто зустрічаються процеси, які мають спільну назву процесів органічної зміни величин. Ця назва пов‘язана із тим, що такі процеси часто зустрічаються в біології. Значна властивість цих процесів полягає в тому, що за однакові проміжки часу значення величини змінюється в одному і тому ж самому відношенні.

Наведемо приклади, в яких величини змінюються за вказаним вище законом:

- задача про радіоактивний розпад;

- задача про зміну атмосферного тиску;

- задача про розмноження бактерій;

- задача про вакуумування;

- задача про приріст деревини.

 

Слайд 11

Якщо людина хоче зібрати гроші, наприклад, для подорожі, або для певної покупки, або для оплати подальшого навчання, то це можна зробити кількома способами. Можна просто відкладати гроші та зберігати їх удома.  А можна покласти гроші в банк на депозитний рахунок (депозит). На покладені на депозит кошти банк виплачує певні відсотки за один рік тримання коштів на рахунку, що збільшує вкладені кошти, і тим самим вкладник отримує прибуток.  Банки пропонують різні види депозитів із різними умовами нарахування відсотків. Один з видів депозиту — депозит з капіталізацією.

Якщо вкладник поклав х гривень на депозит під р відсотків річних не на рік, а на k місяців з капіталізацією кожного місяця, то після закінчення строку депозиту він отримає x · (1 + (p/100)/12)^k гривень.

На уроках інформатики у минулому навчальному році ми з вами розглядали цю тему, проводили відповідні розрахунки. Сама формула нарахування відсотків є показниковою функцією.

 

Слайд 12

Історія показникової функції починається з далеких часів. Термін «показник» (нім. exponent , лат. еxponere – «виставляти напоказ»;  exponens, exponentis – «що виставляється на показ», «той, що показується») для степеня увів у 1553 р. німецький математик (спочатку монах, а потім – професор) Михайль Штифель (1487-1567). Він увів дробові й нульові показники. Позначення а^х для натуральних показників увів Рене Декарт (1637), а вільно поводитися з такими самими дробовими й від’ємними показниками почав із 1676 р. Ісаак Ньютон.

Слайд 13

Степені з довільними дійсними показниками, без будь-якого загального означення, розглядали Лейбніц та Иоганн Бернуллі. 1679 р. Лейбніц увів поняття експоненціальної (тобто показникової) функції для залежності у = а^х та експоненціальної кривої для графіка цієї функції. Коротке найменування «експонента» відображено в одному з позначень: а=ехра х. Через ехр(х) позначається конкретна експонента – з показником а=е=2,71828…, яка введена у велику кількість мов програмування.

Слайд 14

Повідомлення на тему: «Виникнення показникової функції». Нам відома легенда про арабського царя, у якого винахідник шахівниці зажадав за свій винахід зерна. Причому за першу клітку – 1 зерно (2⁰), за другу – два просив винахідник (2¹), за третю – чотири (2²), за четверту – вісім (2³), за п’яту – шістнадцять (2⁴), за шосту – тридцять два (2⁵) і т. д.

Слайд 15

Чимало часу цар витратив на підрахунок. Коли ж підрахували – розплакалися: вийшло вісімнадцять квінтильйонів чотириста сорок шість квадрильйонів сімсот чотири трильйони сімдесят три більйони сімсот дев’ять мільйонів п’ятсот п’ятдесят одна тисяча шістсот п’ятнадцять (число двадцятизначне!). Цього зерна вистачило, щоб засіяти всю сушу та їсти його довелося б мільйони років!

  Слайд 16

Показникова функція описує значну кількість процесів, що відбуваються в природі. Наприклад, зростання кількості бактерій за сприятливих для них умов існування можна описати за законом ().

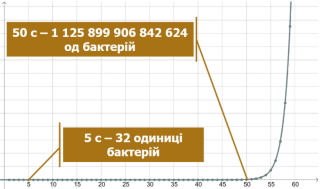
• ЯЯк людина використовує ріст і розмноження бактерій?

(Виробництво антибіотиків, кисломолочних продуктів, виноробство, медицина)

 

 

• Зростання кількості деревини можна порахувати за законом ()

 

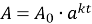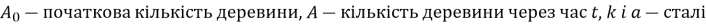• Зменшення маси речовини під час радіоактивного розпаду відбувається за законом 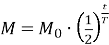( 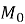– початкова маса речовини, 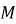– маса в момент часу 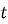, 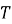– період напіврозпаду речовини (час розпаду половини атомів заданої речовини))

 

• Зменшення тиску повітря з висотою відбувається за законом 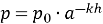( 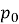– тиск на рівні моря, 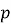– тиск на висоті 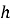, 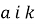- сталі)

 

Отже, показникова функція не випадково народилася, органічно увійшла у життя і знайшла широке застосування. Як бачимо показникові функції трапляються в найрізноманітніших галузях науки — фізиці, хімії, біології, економіці, інформатиці, медицині, лісництві, картографії, будівництві тощо.

Слайд 17

ІІІ. Вивчення нового матеріалу

 

План уроку:

1. Означення показникової функції.

2. Графік показникової функції.

3. Властивості показникової функції.

Слайд 18

Показникова функція

Функція виду називається показниковою.

Наприклад:

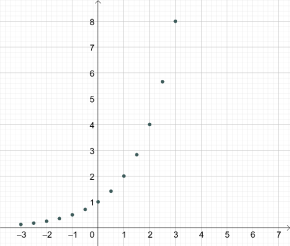
Побудуємо для деяких цілих значень.

 

 

 

 

 

 

 

 

 

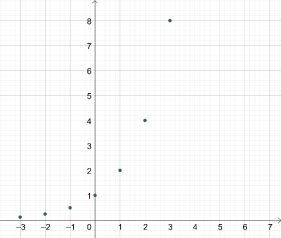
Тепер на цьому ж графіку добудуємо деякі дробові значення функції

 

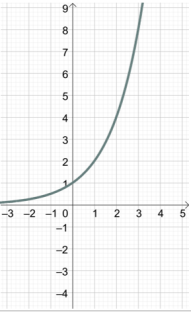
Якщо побудуємо всі значення з множини , то отримаємо графік показникової функції (можливий інший запис, наприклад: ).

 

*Кожна точка цього графіка є степенем числа 2 з дійсним показником .

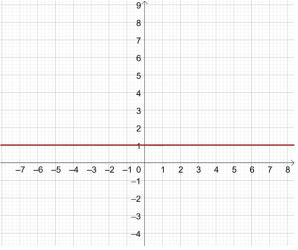
• Чи існує функція при

 

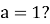
• Існує, але це вже буде не показникова функція. Графіком такої функції є пряма.

 

• Чи може отриманий графік показникової функції перетнути вісь абсцис?

 

• Ні, навіть якщо ми візьмемо від’ємний показник степеня, то завжди отримаємо додатне значення

 

Слайд 19 на екрані

Слайд 20

 

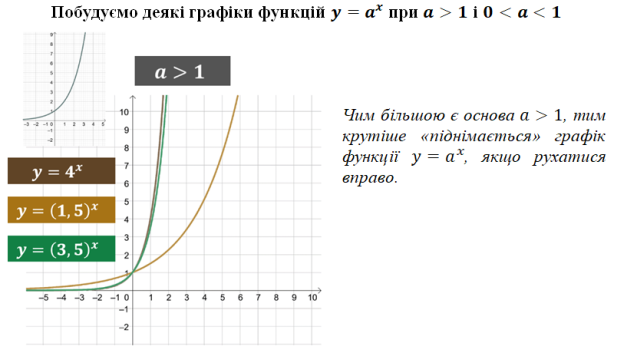
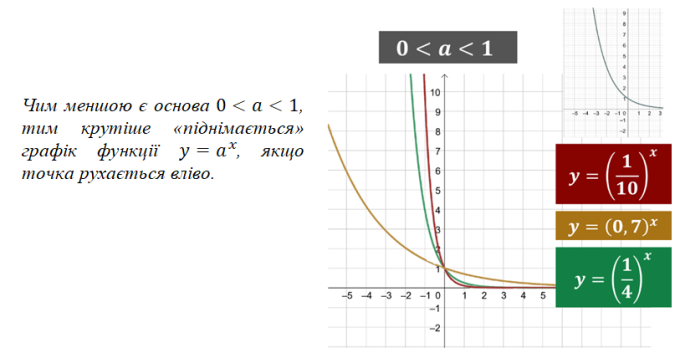
Слайд 21

• Пригадаємо властивості степеня з раціональним показником.

             Всі ці властивості справедливі для та будь- 
            яких дійсних

 

 

Слайд 22

 

Властивості показникової функції

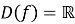1. (Областю визначення показникової функції є множина дійсних чисел)

 

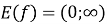2. (Областю значень показникової функції є множина )

 

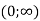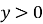3. при всіх значеннях 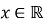(Показникова функція немає нулів, і проміжок 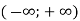є проміжком її знакосталості)

 

4. При 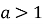зростаюча (При 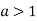зростає на всій області визначення)

При спадна (При спадає на всій області визначення)

 

IV. Закріплення нових знань та вмінь учнів

Слайд 23

№1

Яка з даних функцій є показниковою:

 

Слайд 24

№ 2

Ґрунтуючись на які властивості показникової функції можна стверджувати, що:

?

 

Відповідь: При показникова функція є зростаючою, при – спадною.

Слайд 25

№ 3

Які з наведених показникових функцій є зростаючими, а які — спадними:

а) y = ^x ;     б) y = (0,5)^x;  в) у = ; г) y = 2^-x

слайд 26

№ 4

Порівняйте:

 

 

Слайд 27

Давайте розглянемо, як нам можуть знадобитися знання показникової функції при вивченні предмету «Технологія приготування їжі з основами товарознавства».

Прикладом швидкого розмножування бактерій є виготовлення дріжджів, під час якого по мірі росту бактерій проводиться відповідне додавання цукрової маси. Відомо, що збільшення маси дріжджів виражається формулою показникової функції m=m₀1,2^t, де m₀ – початкова маса дріжджів, t – час бродіння в годинах, m – маса дріжджів в процесі бродіння.

Знайти масу дріжджів, якщо початкова маса складає 10 кг, а тривалість процесу 9 год.

Підставивши наші дані у формулу, отримаємо приблизну відповідь

m=101,2⁹  51,6 кг.

 

Слайд 28

Відповідаємо.

1. Яку функцію називають показниковою?
2. Чи може показникова функція перетнути вісь абсцис?
3. Які властивості має степінь з дійсним показником?
4. Через яку точку проходять всі графіки всіх показникових функцій?
5. За якої умови показникова функція зростає? А за якої – спадає?
6. Чи може значення показникової функції бути від’ємним?
7. Чи може значення показникової функції дорівнювати нулю?

 

V. Підведення підсумків уроку ( рефлексія).

Мета етапу: Визначити чи досягнуті, мета, очікувані результати уроку,  

                          провести рефлексію.

Слайд 29

 

Учням пропонується закінчити речення

1. Було цікаво…

2. Було важко…

3. Я навчилась…

4. У мене вийшло…

 

Таким чином, для успіху потрібно: «самоконтроль», «співпраця», «досконала підготовка». Але протягом уроку ми весь час працювали з партнерами, могли отримати допомогу, а в житті дуже часто випадає розраховувати на свої сили. І цього теж потрібно вчитись. Це одна з причин виконання домашніх завдань.

 

Слайд 30

VІ. Домашнє завдання.

Істер О.С. Математика 11

Опрацювати §1

Виконати № 1,5; 1.7; 1.13;

 

Слайд 31 

Висновок:

Чи існує універсальна форма успіху, чи одержали ми її сьогодні на уроці? Це питання належить до розряду проблем, пошуку філософського каменя, створення вічного двигуна, побудови машини часу. Але без віри людини у можливість у їх створення, не було б кроку вперед, не було б прогресу.

Хочу подякувати вам за урок, ще раз побажати успіху і сказати, що я вірю у ваш успіх. На згадку про наше заняття запам’ятайте ще один рецепт успіху: „Успіх - це тільки 10% таланту і 90% щоденної наполегливої праці."

 

Притча:

Ішов Мудрець, а назустріч йому три чоловіки, які везли під гарячим сонцем візки з камінням для будівництва. Мудрець зупинився і задав кожному запитання. У першого запитав «Що ти робив цілий день?». І той відповів, що цілий день возив це важке каміння. У другого запитав мудрець «А що ти робив цілий день?», і той відповів: «А я добросовісно виконував свою роботу». А третій посміхнувся, його обличчя засвітилося радістю і задоволенням: «А я приймав участь у будівництві храму!»

І ми сьогодні на уроці приймали участь у будівництві храму – храму науки.

Бажаю всім ще кращих результатів. Дякую за роботу!