Розробка уроку на тему:"Розв'язування однорідних тригонометричних рівнянь"

Тема уроку: Розв'язування однорідних тригонометричних рів­нянь.

Мета уроку: Познайомити учнів з розв'язанням однорідніх тригонометричних рівнянь, створити умови для формування вмінь та навичок учнів самостійно поглиблювати знання, застосовувати їх у практичній діяльності. Розвивати пізнавальну активність учнів; логічне та аналітичне мислення, інтерес до вивчення теми. Виховувати увагу, старанність, культуру математичної мови та запису, впевненість у своїх силах.

Тип уроку : Засвоєння знань, умінь та навичок.

Обладнання : Комп’ютер, картки-завдання.

Девіз уроку :   «Ми ніколи не станемо математиками, навіть знаючи напам’ять усі чужі доведення, якщо наш розум нездатний самостійно розв’язувати які б то не було проблеми»                             Рене Декарт                                                                                          

Хід уроку :

І. Організаційний етап

ІІ. Перевірка домашнього завдання

(За необхідності учитель відповідає на запитання, які виникли у ході виконання домашнього завдання)

ІІІ. Актуалізація опорних знань

Виконання тестових завдань

1) Назвіть значення а, при яких рівняння sin t = a має:

а) має один корінь; б) жодного кореня; в) нескінчену множину коренів.

2) Які з наведених тригонометричних рівнянь є найпростішими, а які ні і чому:

 а) 2cosx =-1;  б) sin x=1;    в) 4tgx=3;     г) ctg(2x/3)=0 ?

3) Яке з наведених рівнянь не має розв'язків:

    a) sin x=3/7;     б) tg x=5;  в) cos x=5/2;     г) ctg x=-10  ?

4) Коренем рівняння tg x =a  є   t = … .

5) Яка рівність є правильною:

    а) cos(-x) = cos x;  б)  arcsin(-x) =  arcsin x;  в)  arctg(-x)=arctg x  ?

6) Розв'яжіть рівняння sin x=1/2.

    а) (-1) + 2n , n  ; б) (-1) + n , n  ; в) + 2n , n  ;                  г)  + 2n , n  

7) Знайдіть помилку:

    а) tg x ctg x = 1;   б) cos² - cos2 = - sin²;   в) 2sin x cos x = sin 2x;   

г)

 

 

IV. Формування теми, мети й завдань уроку

V. Сприймання і усвідомлення нового матеріалу

 

1. Розглянемо рівняння виду asin x + bcos x = 0 (однорідне рів­няння 1-го степеня), де а і b не дорівнюють нулю. Значення x, при яких cos x дорівнює нулю, не задовольняє даному рівнянню, бо тоді і sin x теж дорівнював би нулю, а cos x і sin x не можуть одночасно дорівнювати нулю. Тому можна розділити обидві частини рівняння почленно на cos x. Маємо:

        atg x + b = 0      tg x = - .

x = - arctg + πn, n Z.

Приклад 1 Розвяжіть рівняння:  3 sin x + cos x = 0

Розвязання:

Оскільки корені рівняння соs х = 0 не є коренями початкового рівняння, то соs х ≠ 0

 3

3 tg x + 1 = 0

tg x = -

x = - + n , n  

Відповідь: x = - + n , n  

2. Рівняння виду  a sin²x + b sinx cosx + c cos²x = 0 називається однорідним рівнянням 2-го степеня. Якщо числа а, b, с не дорівнюють нулю, то розділимо дане рівняння на cos² x (або на sin²x). (У даному рівнянні cos²x ≠ 0, бо в супротивному випадку sin² x теж дорівнював би нулю, а cos x і sin x не можуть одночасно дорівнювати нулю). Тоді

;  

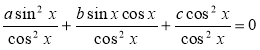atg²x + btgx + c = 0.

 

Розв'язавши отримане, рівняння одержимо корені даного рів­няння.

Приклад 2 Розвяжіть рівняння:   3sin² x + sin x cos x = 2 cos² x

Розвязання:

3sin² x + sin x cos x = 2 cos² x

3sin² x + sin x cos x - 2 cos² x = 0

3tg²x + tgx - 2 = 0, тому що cos²x ≠ 0

 

tg x = -1 ; x = -+ πk, k 

tg x = ; x = arctg + πn, пZ.

Відповідь: -+ πk, k  ; arctg + πn, пZ

3. Рівняння виду

а_n sinⁿ x + a_n-1 sin^n-1x cos x +... + a₁ sinx cos^n-1x + a₀ cosⁿ x = 0

називається однорідним рівнянням п-го степеня відносно си­нуса і косинуса.

Якщо жоден із коефіцієнтів a_n, а _n-1, ... , а₁, a₀ не дорівнює нулю, то, розділивши обидві частини рівняння почленно на cosⁿx, одержимо рівняння n-го степеня відносно tgx. Якщо хоча б один із коефіцієнтів a_n, а _n-1, ... , а₁, a₀ дорівнює нулю, то перш ніж виконувати ділення на cosⁿx, слід довес­ти, що cosⁿx ≠ 0, тобто, cos x ≠ 0.

 

Приклад 3 Розвяжіть рівняння: cos² x - 2 cos x sin x = 0.

Ділити обидві частини на cos² x не можна, бо cos² x = 0 є роз­в'язком даного рівняння. Це рівняння можна розв'язати:

 

І спосіб (винесення множника)

cos² x – 2 cos x sin x = 0  cos x (cos x – 2 sin x) = 0

Звідси cosx = 0 або cosx – 2sinx = 0.

1) cos x = 0; x = + πп, пZ.

2) cosx – 2sinx = 0; ; l – 2tgx = 0; tgx = ; x = arctg + πn, пZ.

Відповідь:  + πn, пZ; arctg + πn, пZ.

 

II спосіб. Розділимо обидві частини на sin² x, оскільки sin x ≠ 0 в даному рівнянні, бо в супротивному випадку і cos x = 0, що неможливо.       

,

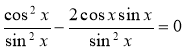ctg² x - 2ctg x = 0;

ctgх(ctg x - 2) = 0.

Звідси ctg x = 0, або ctg x = 2.

1. ctg x = 0; x = 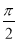+ πп, п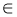Z.  
2. ctg x = 2; x = arcctg 2 + πn, п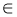Z.

Відповідь: + πn, arcctg 2 + πn, пZ.

VІ. Закріплення вмінь і навичок

Виконання письмових вправ

1.Середній рівень       Розвяжіть рівняння:

а) 4 sin² x - sin 2х =3                             б) sin2 x +4соs²х =1     

Розвязання:

а) 4 sin² x - sin 2х - 3 = 0

 4 sin² x - 2sin х cos x - 3 = 0

4 sin² x - 2sin х cos x = 3 (sin² x + cos² x)

sin² x - 2sin х cos x - 3 cos² x = 0

Одержали однорідне рівняння 2-го степеня. Розділимо обидві частини рівняння на cos²x ≠ 0 (оскільки, якщо cos x = 0, то й  sin х = 0, що неможливо одночасно)

tg²x -2 tgx - 3 = 0

tgx = t;   t² - 2 t - 3 = 0;  t = 3;  t = -1

tgx = 3     х = аrctg 3 + k, k

tgx = -1    x= -+ πn, n 

Відповідь:-+ πn, arcctg 3 + πk, n, kZ.

 

б) sin2 x +4соs²х =1

2sin x cos x +4соs²х = sin² x +cos² x

 sin² x - 2sin x cos x - 3 sin² x =0 (:cos² x≠0)

tg²x -2 tgx - 3 = 0

tgx = t

t² - 2 t - 3 = 0

t = 3;  t = -1

tgx = 3     х = аrctg 3 + k, k

tgx = -1    x= -+ πn, n

Відповідь:-+ πn, arcctg 3 + πk, n, kZ.

2. Високий   рівень    Розвяжіть рівняння:

2 sin x cos²( - x) +3соs²( + х) соs х - 5cos² x sin x ( + x)= 0

Розвязання:

2 sin³ x +3 sin² x соs х - 5cos^³ x = 0 (:cos² x≠0)

2 tg³ x +3 tg² x - 5 = 0

tg x = t; 2t³ +3t² - 5 = 0

2t³ -3t² +5t² - 5 = 0

2t²  (t -1)+ 5 (t - 1)( t  + 1) = 0

t -1=0                                                         або    2t² +5t + 5 = 0

t =1;    tgx = 1    x= + πn, n               D = 25 – 40 = -15 <0    коренів немає

Відповідь:-+ πn, nZ.

VІІ. Підбиття підсумків уроку

Запитаня до класу

1. Яким способом розвязуються однорідні тригонометричні рівняння?

2.Що необхідно перевіряти під час розвязування однорідних тригонометричних рівнянь?

 

VІІІ. Домашнє завдання

1. Опрацювати § 28

2. Виконати  ІДЗ:

Розвяжіть рівняння,  де  A  ваш порядковий номер у класному журналі

1.(3 A +1) cos² ( + x) – 0,5(3 A -1)  sin 2x  = 3 A

Відповідь:-+ πn, arcctg 3A +  πk, n, kZ.

2. (1 + 5 A) cos²  x  – 0,5(1 - 5 A)  sin 2x  = 1  

 

Відповідь:-+ πn, arcctg 5A + πk, n, kZ.

 

 

 

 

 

 

 

 

Список використаних джерел

1. Бурда М.І., Мальований Ю.І.,Дубинчук О.С. Математика.10-11.-К.:Освіта,2006.-512с.

2.Роганін О.М. Алгебра і початки аналізу:10 клас:Плани-конспекти уроків.-Х.:Світ дитинства,2002.- 256с.

3. Цуренко С.П.  Математика 10 клас - Т .: Навчальна книга-Богдан, 2001.-64с.