Конспект уроку на тему "Системи 2 рівнянь з двома змінними як математична модель прикладної задачі. Розв’язування задач і вправ"

          Богдан Юлія

Урок №35        Дата ___________

Тема: Системи 2 рівнянь з двома змінними як математична модель прикладної задачі. Розв’язування задач і вправ.

Мета:

Навчальна: закріпити поняття про системи 2 рівнянь з двома змінними, сформувати вміння за текстом задачі складати та розв’язувати системи 2 рівнянь з двома змінними;

Розвивальна: розвинути в учнів логічне мислення, вміння встановлювати взаємозв’язки у отриманій інформації;

Виховна: виховувати розуміння ролі математики в житті, розуміння важливості математичних знань.

Обладнання: Підручник з математики 9 клас (Мерзляк).

Хід уроку

1. Організаційний етап

• Привітання
• Перевірка присутності учнів на уроці
• Перевірка готовності учнів та кабінету до уроку

2. Перевірка домашнього завдання

Чи є в когось запитання до домашнього завдання? Якщо є запитання, то відповідаю на них, якщо ж ні, то учні відкривають зошити, записують число, класна робота, тему уроку: «Системи 2 рівнянь з двома змінними як математична модель прикладної задачі. Розв’язування задач і вправ». А в цей час я перевіряю наявність домашнього завдання проходячи між рядами.

3. Актуалізація опорних знань

1. Закінчіть речення: «Системою 2 рівнянь другого степеня з 2 змінними називається … »
2. Що означає розв’язати систему?
3. Які є способи розв’язання систем 2 рівнянь з двома змінними?
4. Які переваги та недоліки кожного з методів розв’язування систем 2 рівнянь з двома змінними?

Сьогодні ми продовжимо розв’язувати прикладні задачі за допомогою систем 2 рівнянь з 2 змінними.

4. Вправи для закріплення

№ 14.21 (Алгебра 9 клас Мерзляк)

Розв’язання: Нехай х (х>0) год потрібно щоб наповнити басейн з 1 труби, тоді

у (y>0) год потрібно щоб наповнити басейн з 2 труби.

частина басейну заповнюється з 1 труби за 1 год;

частина басейну заповнюється з 2 труби за 1 год;

За 12 годин 1 труба наповнить частину басейну, а 2 - частину басейну. За умовою за 12 годин одночасної роботи двох труб басейн буде повний. Маємо рівняння: .

У другому випадку за 5 год 1 труба наповнить басейн на , а 2 труба за 9 год наповнить басейн на . За умовою задачі після такої роботи басейн буде наповнено на половину, отже маємо рівняння: . Отримали систему рівнянь:

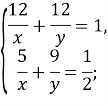
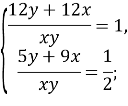
Отже 16 год потрібно щоб наповнити басейн з 1 труби і 48 год щоб наповнити басейн з 2 труби.

Відповідь: 16 год, 48 год.

Методичний коментар: для того щоб розв’язати дану задачу слід встановити взаємозв’язки між її даними та побудувати математичну модель у вигляді системи 2 рівнянь з 2 змінними. Розв’язком задачі будуть розв’язки утвореної системи. Для розв’язання системи слід спочатку застосувати метод порівняння. Для цього перетворити рівняння так, щоб їх праві (ліві) частини були рівними, прирівняти відмінні частини та виразити одну змінну через іншу. Далі застосувати метод підстановки (заміни змінної). Знайшовши розв’язок системи перевірити чи він задовільняє умови накладені на змінні (ОДЗ). Записати відповідь на запитання задачі.

№ 14.23 (Алгебра 9 клас Мерзляк)

Розв’язання: Нехай х Ом – опір 1 провідника, тоді

у Ом – опір 2 провідника.

При послідовному з’єднані 2 провідників їх опори додається, тому маємо рівняння: .

При паралельному з'єднанні провідників опір системи рахуюит за формулою . Маємо рівняння: .

Отримали систему рівнянь:

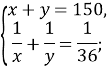
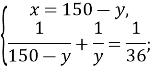
ОДЗ:

Так як порядок з’єднання провідників для обчислення опору у даних випадках не важливий то опвр 1 провідника 90 Ом, а 2 – 60 Ом.

Відповідь: 90 Ом, 60 Ом.

Методичний коментар: для того щоб розв’язати дану задачу слід пригадати раніше вивчений матеріал із фізики, а саме властивості з’єднання провідників. Після цього встановити взаємозв’язки між даними задачі та побудувати її математичну модель – систему рівнянь. Систему рівнянь розв’язати методом підстановки. Для утвореного дробово-раціонального рівняння вказати ОДЗ та звести його до квадратного. Застосувавши дискримінант знайти корені квадратного рівняння, перевірити чи входять вони в ОДЗ. Повернутися до заміни та знайти 2 невідоме значення. Записати відповідь на запитання задачі.

№ 14.25 (Алгебра 8 клас Мерзляк)

Розв’язання:

Нехай х км/год (x>0) – власна швидкість човна, тоді

у км/год (y>0) – швидкість течії,

х+у км/год – швидкість човна за течією,

х-у км/год – швидкість човна проти течії.

Використовуючи співвідношення між часом відстанню та швидкістю маємо, що відстань з пункту А до пункту В за течією човен подолає за год, а проти течій за год. За умовою задачі шлях з п.А до п.В і назад зайняв 6 год. Маємо рівняння: .

2 км за течією човен подолає за год, а 1 км проти течії – за год. За умовою задачі ці інтервали часу рівні, тому маємо рівняння: .

Маємо систему:

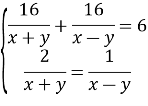
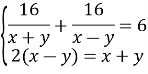
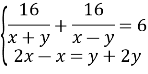
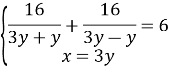
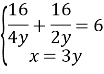
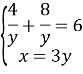
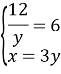
Отже швидкість течії – 2 км/год.

Відповідь: 2 км/год.

Методичний коментар: для того щоб розв’язати дану задачу слід пригадати раніше вивчений матеріал із фізики, а саме, що таке швидкість та особливості руху за та проти течії річки. Після цього встановити взаємозв’язки між даними задачі та побудувати її математичну модель – систему рівнянь. Систему рівнянь розв’язати методом підстановки. Записати відповідь на запитання задачі.

№ 14.30 (Алгебра 9 клас Мерзляк)

Розв’язання:

Нехай х г/см³  (x>0)– густина 1 зливка,

у г/см³ (y>0)– густина 2 зливка.

За умовою задачі відомо, що густина 1 зливка на 2 г/см³ більша ніж густина 2 зливка, отже маємо рівняння: .

Користуючись формулою, що виражає співвідношення між густиною, масою та об’ємом, знайдемо об’єм кожного зливка: см³ – об’єм 1 зливка, см³ – об’єм 2 зливка. За умовою задачі відомо, що об’єм 1 зливка на 10 см³ менший за об’єм 2 зливка, з цього маємо рівняння: .

Отримали систему рівнянь:

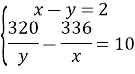
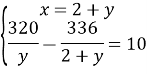
– сторонній корінь, так як він суперечить умові накладеній на у (у>0).

Отже густина 1 зливка 8,4 г/см³, а густина 2 зливка 6,4 г/см³.

Відповідь: 8,4 г/см³, 6,4 г/см³.

Методичний коментар: для того щоб розв’язати дану задачу слід пригадати раніше вивчений матеріал із фізики, а саме, що таке густина та як вона пов’язана з масою та об’ємом. Після цього встановити взаємозв’язки між даними задачі та побудувати її математичну модель – систему рівнянь. Систему рівнянь розв’язати методом підстановки. Для утвореного дробово-раціонального рівняння вказати ОДЗ та звести його до квадратного. Застосувавши дискримінант знайти корені квадратного рівняння, перевірити чи входять вони в ОДЗ. Повернутися до заміни та знайти 2 невідоме значення. Записати відповідь на запитання задачі.

5. Підбиття підсумків уроку

• Що нового ви дізналися сьогодні на уроці?
• Що було для вас уже відомим?
• Що було цікавим на уроці?
• Над чим ще варто попрацювати?

6. Домашнє завдання

§ 14 № 14.24; 14.26.