Конспект уроку "Показникова функція"
Тема: Показникова функція.
Мета:
- узагальнити та систематизувати знання й навички учнів з теми «Показникова функція»;
- розвивати логічне мислення, навички колективної та самостійної роботи, уміння розраховувати свої сили і оцінювати свої можливості, спонукати до самоконтролю, взаємоконтролю;
- виховувати культуру математичної мови, наполегливість, самостійність, контролювати увагу на всіх етапах уроку.
Тип уроку: урок узагальнення й систематизації знань.
Обладнання:
- презентація;
- вислови;
- таблиця-стенд;
- завдання для самостійної роботи;
- бланки для відповідей
Х І Д У Р О К У
І. Мотивація навчання.
Сьогодні на уроці ми повинні узагальнити та систематизувати знання з теми «Показникова функція», закріпити й відкоригувати уміння й навички розв’язувати показникові рівняння та нерівності. І.Хіксон говорив: «Якщо відразу не має успіху, то спробуйте ще і ще». Тому не слід розчаровуватися при можливих невдачах. Обчислюйте, міркуйте раціонально, пам’ятайте, що швидкість потрібна, будьте уважні. Кожен з вас має бланк відповідей, який треба заповнити протягом уроку.
ІІ. Актуалізація навчальної діяльності учнів.
- Чи є запитання по виконанню домашнього завдання? (Якщо є, даю відповіді разом з учнями)
- Повторення теоретичного матеріалу за допомогою презентації.
-
Яка функція називається показниковою? Чому в означенні сказано, що а > 0 і а
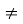 1?
1?
-
Назвати область визначення функції у =
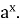
-
Які властивості має функція у =
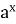 , якщо а > 1?
, якщо а > 1?
- Сформулювати властивості показникової функції, якщо 0<a<1.
- Як називається графік показникової функції?
-
Що можна сказати про числа p і q, якщо
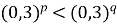 ?
?
-
Що можна сказати про додатну основу а , якщо
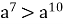 ?
?
ІІІ. Узагальнення й систематизація знань.
- Виконання тестових завдань з занесенням у бланк відповідей
Варіант1
- Яка з наведених функцій є показниковою?
|
а |
б |
в |
г |
|
|
|
у=2х+6 |
|
- Яка з наведених функцій є спадною?
|
а |
б |
в |
г |
|
|
|
|
|
-
Розв'яжіть рівняння
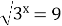
|
а |
б |
в |
г |
|
4 |
2 |
0,5 |
1 |
-
Розв'яжіть нерівність
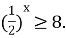
|
а |
б |
в |
г |
|
|
|
|
|
Варіант 2
- Яка з наведених функцій є показниковою?
|
а |
б |
в |
г |
|
|
у = -х |
у = 6 |
|
2.Яка з наведених функцій є зростаючою?
|
а |
б |
в |
г |
|
|
|
|
|
3.Розв'яжіть рівняння ![]()
|
а |
б |
в |
г |
|
2 |
4 |
1 |
-2 |
4. Розв'яжіть нерівність ![]() .
.
|
а |
б |
в |
Г |
|
|
|
|
|
2.Показникові рівняння
- Які рівняння називаються показниковими?
- Які види найпростіших показникових рівнянь вам знайомі?
-
Чи має розв'язок рівняння
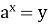 , якщо у < 0?
, якщо у < 0?
- Які основні способи розв'язування показникових рівнянь?
-
Розв'яжіть рівняння (учениця біля дошки)
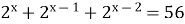 .
.
-
(Завдання ЗНО). Розв'яжіть рівняння
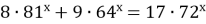 . У відповідь запишіть суму коренів рівняння.
. У відповідь запишіть суму коренів рівняння.
- Фізкультхвилинка.
Пригадайте зображення графіка показникової функції , якщо вона зростає. Покажемо його рухами (плавно показуємо разом ). А зараз будьте уважні. Я називаю вам функцію , а ви показуєте рухами її графік. у = ![]() , у =
, у = ![]() .
.
- Показникові нерівності
- Які нерівності називаються показниковими?
- Що треба враховувати при розв'язанні показникових нерівностей?
-
Розв'яжіть нерівність (біля дошки)
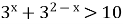 .
.
-
(Завдання ЗНО). Розв'яжіть нерівність
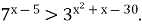
- Виконання завдань із занесенням у бланк відповідей
Варіант 1.
- (з відкритою відповіддю) . Розв'яжіть нерівність.
![]() У відповідь записати суму всіх розв'язків нерівності.
У відповідь записати суму всіх розв'язків нерівності.
- (з розгорнутим розв'язанням). Розв'яжіть рівняння.
![]()
Варіант 2.
- (з відкритою відповіддю). ). Розв'яжіть нерівність
![]() У відповідь запишіть найбільший цілий розв'язок.
У відповідь запишіть найбільший цілий розв'язок.
- (з розгорнутим розв'язанням). Розв'яжіть рівняння
![]()
IY. Підсумки уроку.
Рефлексія.
- Яке завдання було найскладнішим? Найлегшим? Найцікавішим?
- Взаємоперевірка завдань самостійної роботи за готовими відповідями.
- Виставлення оцінок.
Y. Домашнє завдання
При яких значеннях параметра а рівняння ![]() має єдиний корінь?
має єдиний корінь?


про публікацію авторської розробки
Додати розробку
