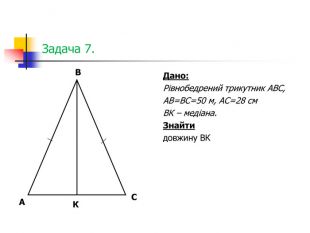
Конспект уроку + презентації на тему: «Теорема Піфагора та її практичне застосування».
У цій розробці Ви зможете ознайомитися з конспектом уроку на тему: «Теорема Піфагора та її практичне застосування» та переглянути презентації учнів.
- Піфагора.Ариніч Марина 8-ФМ.ppt ppt
- Теорема Піфагора.docx docx
- уроку.ppt ppt
- .pptx pptx
Конспект уроку на тему "Теорема Піфагора"
Мета: з'ясувати з учнями зміст теореми Піфагора та її доведення; формувати вміння застосовувати теорему до розв'язування задач; розвивати логічне мислення, культуру мовлення; виховувати інтерес учнів до історичних цінностей.
Тип уроку: засвоєння нових знань.
Обладнання: нитка з вузликами, плакати, проектор, роздатковий матеріал.
ХІД УРОКУ
І. ОРГАНІЗАЦІЙНИЙ МОМЕНТ
II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ
Фронтальне опитування
1. Сформулюйте ознаки подібності трикутників.
2. Що випливає з подібності трикутників?
Закінчи речення:
1. Сторони прямокутного трикутника називають...
2. Більшу сторону прямокутного трикутника називають...
3. Менші сторони прямокутного трикутника називають...
4. Площа квадрата дорівнює...
5. Площа квадрата зі стороною Ь дорівнює...
III. МОТИВАЦІЯ НАВЧАЛЬНОЇ ДІЯЛЬНОСТІ
За допомогою мотузки зробити прямокутний трикутник. Тобто в прямокутному трикутнику існують залежності між сторонами . Сьогодні ми вивчимо і доведемо теорему Піфагора, яка точно вкаже залежність катетів і гепотенузи.
IV. ПОВІДОМЛЕННЯ ТЕМИ ТА МЕТИ УРОКУ
V. СПРИЙМАННЯ ТА ЗАСВОЄННЯ НОВОГО МАТЕРІАЛУ
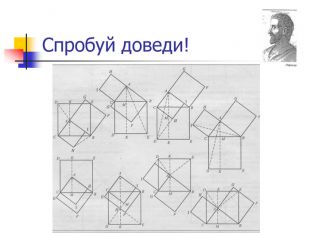
Сьогодні на уроці ми ознайомимось із сучасним формулюванням теореми Піфагора та ним зі способів її доведення (їх існує понад 150).
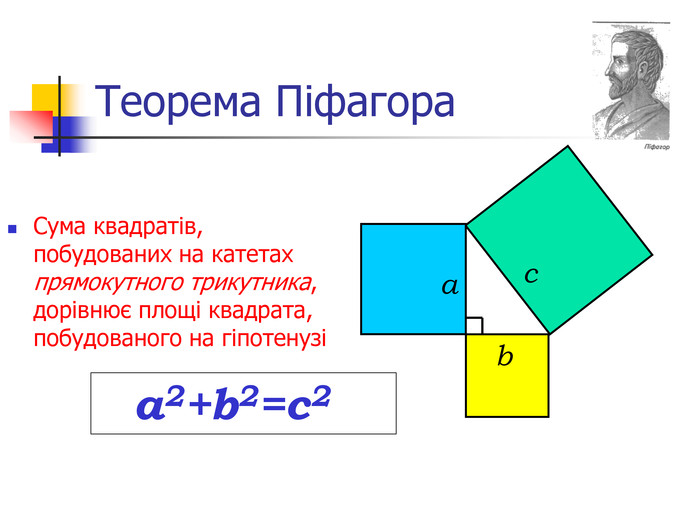
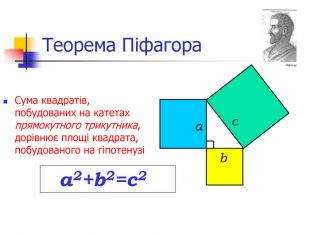
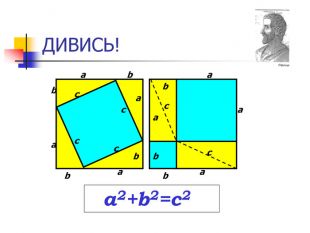
1. Формулювання теореми Піфагора.
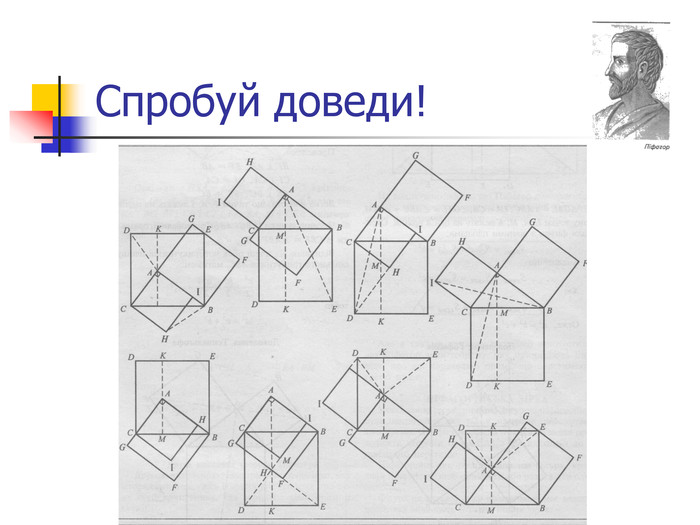
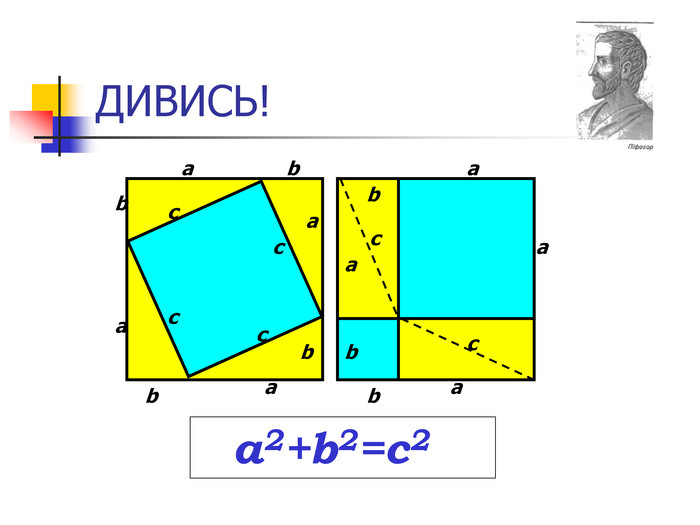
2. Доведення теореми одним зі способів, а саме з використанням властивості висоти.
VI. УСВІДОМЛЕННЯ ЗНАНЬ
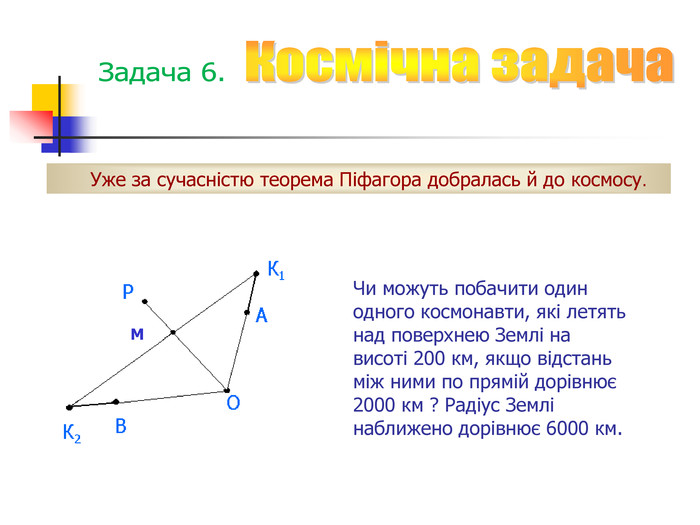
Розв’язування історичних задач презинтації.
VII. УЗАГАЛЬНЕННЯ ТА СИСТЕМАТИЗАЦІЯ ЗНАНЬ
1) Для якого трикутника справедлива теорема Піфагора?
2) Якими формулами пов'язані між собою сторони прямокутного трикутника?
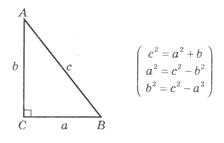
3) Порівняйте гіпотенузу з катетами і навпаки.
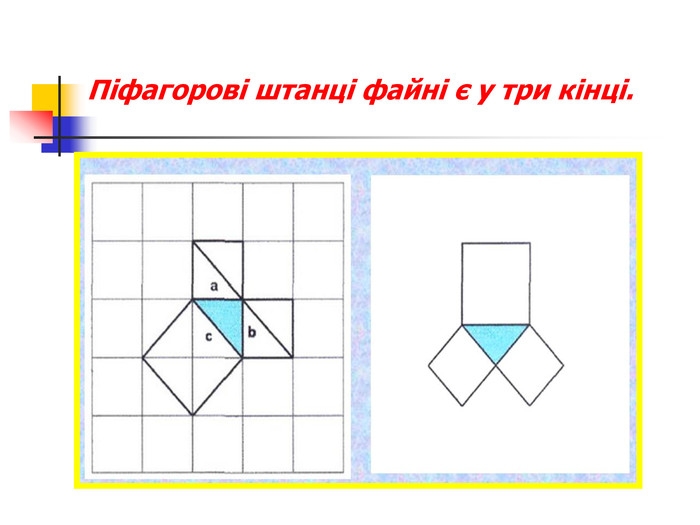
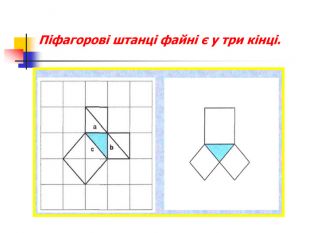
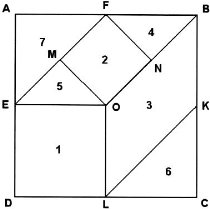 «ПИФАГОРОВА ГОЛОВОЛОМКА»
«ПИФАГОРОВА ГОЛОВОЛОМКА»
Квадрат розрізати на 7 геометричних фігур, а потім учням пропонується знову скласти квадрат.
VIII. ПІДСУМОК УРОКУ
Сьогодні на уроці я дізналась (дізнався)...
IX. ДОМАШНЄ ЗАВДАННЯ
Вивчити теорію. Довести теорему відмінну способом до доведення в класі.
Розв'язати задачі № 23.10, 23.9, 23.20.


про публікацію авторської розробки
Додати розробку