Конспект уроку+ презентація "Додавання векторів"
Розробка уроку з геометрії 9 клас на тему: "Додавання векторів"
Комплект: презентація і конспект уроку.
Тема: Додавання векторів
Мета: вдосконалити та доповнити знання учнів про вектор; ввести поняття суми двох векторів, розглянути закони додавання векторів, навчити будувати суму двох даних векторів, використовуючи правило трикутника і паралелограма; розвивати логічне мислення, вміння переносити знання в нестандартні ситуації; виховувати культуру математичного запису, охайність математичних побудов.
Тема. Додавання векторів
Мета: вдосконалити та доповнити знання учнів про вектор; ввести поняття суми двох векторів, розглянути закони додавання векторів, навчити будувати суму двох даних векторів, використовуючи правило трикутника і паралелограма; розвивати логічне мислення, вміння переносити знання в нестандартні ситуації; виховувати культуру математичного запису, охайність математичних побудов.
Обладнання: конспект уроку, презентація до уроку, підручник геометрія 9 клас, А.П.Єршова, В.В.Голобородько, О.Ф.Крижановський, С.В.Єршов.
Тип уроку: комбінований.
Вимоги до рівня підготовки учнів: описують алгоритм додавання векторів, відкладають вектор, що дорівнює сумі векторів; формулюють властивості суми векторів; застосовують вивчені властивості й означення до розв’язування задач.
ХІД УРОКУ
І. Організаційний момент.
Відмітити відсутніх в класі. Перевірити підготовку учнів до уроку (наявність робочого зошита, щоденника, олівця, лінійки).
ІІ. Перевірка домашнього завдання.
Учні-контролери перевіряють перевіряють виконане домашнє завдання за готовими розв’язками.
ІІІ. Актуалізація опорних знань.
Вправа: «Морський бій»
- Що таке вектор?
а) вектор – це напрямлений відрізок;
б) вектор – це відрізок, що має координати;
в) вектор – це пряма, що має напрям.
- Нульовий вектор – це…
а) вектор, абсолютна величина якого не існує;
б) вектор, у якого початок співпадає з його кінцем;
в) вектор, що не має ні початку, ні кінця.
- Які вектори називаються колінеарними?
а) якщо вони не лежать на одній прямій;
б) якщо вони лежать на одній прямій або паралельних прямих;
в) якщо вони не паралельні одній прямій.
- Які два вектори є рівними?
а) якщо вони співнапрямлені;
б) якщо вони мають рівні довжини;
в) якщо вони співнапрямлені і мають рівні довжини.
- Вектори зображені на рисунку
![]()
![]() а) колінеарні;
а) колінеарні;
б) рівні;
в) протилежні.
-
На площині позначено точки A і B. Якими є вектори
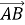 і
і 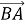 ?
?
а) рівні;
б) мають одинакові довжини;
в) співнапрямлені.
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
а |
Н |
Ф |
Ш |
С |
Я |
Е |
|
б |
В |
А |
П |
Ю |
Г |
М |
|
в |
Д |
Б |
У |
Р |
Ю |
Х |
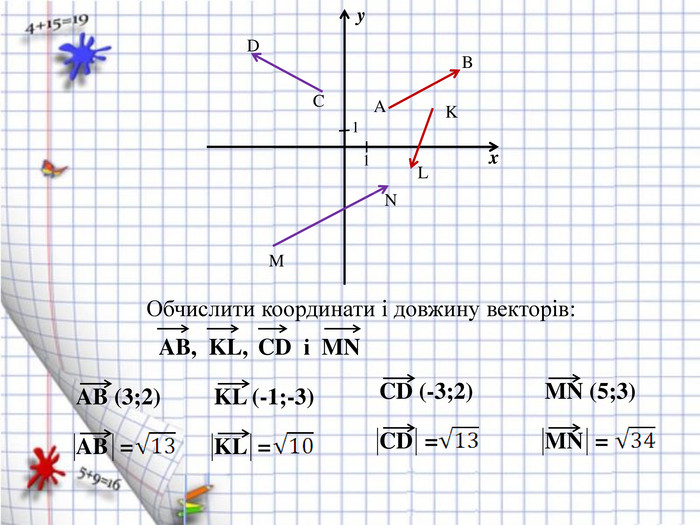
Практична вправа: Двоє учнів виконують завдання на дошці, інші у зошит.
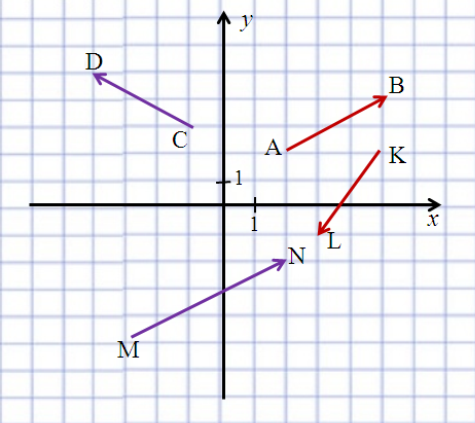
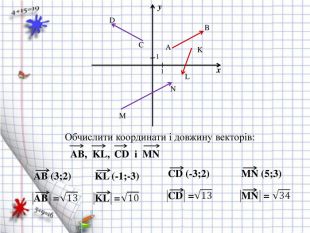
Координати вектора ![]() Координати вектора
Координати вектора ![]()
Довжину векторів ![]() Довжину векторів
Довжину векторів ![]()
ІV. Мотивація навчальної діяльності. Постановка завдань, мети уроку.
Всі ми знаємо байку І.А.Крилова: «Лебідь, Щука і Рак». На вашу думку чому вони так і не змогли потягнути того возика?
Відповідь на це запитання ми можемо знайти у фізиці та геометрії.
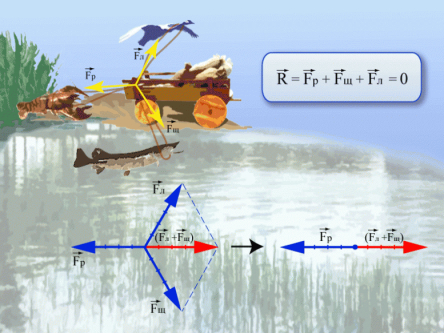
Дивлячись на цей малюнок я думаю ви змогли впізнати тільки нове для себе поняття «вектор», а от що з ним робили, я думаю ви не здогадуєтесь.
Сьогодні на уроці ми доповнимо наші знання про вектор і розглянемо як можна додавати вектори, з’ясуємо, що є сумою векторів. Навчимося будувати суму векторів та знаходити координати суми векторів.
V. Пояснення нового матеріалу.
Означення. Сумою векторів ![]() і
і ![]() називається вектор
називається вектор ![]() з координатами
з координатами ![]() ,
, ![]() .
.
А зараз, розглянемо додавання векторів з фізичної точки зору.
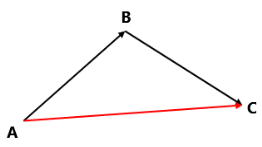
|
Нехай матеріальна точка перемістилась з точки A в точку B, а потім з точки B в точку C. У результаті цих двох переміщень матеріальна точка перемістилась з |
|
точки A в точку C.
Оскільки переміщення з точки A в точку C складається з переміщення з A в B і переміщення з B в C, тобто вектор ![]() природно називати сумою векторів
природно називати сумою векторів ![]() і
і ![]() :
: ![]()
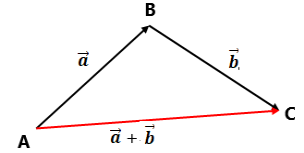
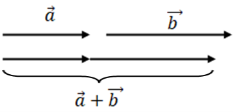
Правило додавання векторів (правило трикутника):
Нехай ![]() і
і ![]() – два вектори. Позначимо довільну точку
– два вектори. Позначимо довільну точку ![]()
![]()
![]() . Потім від точки
. Потім від точки ![]()
![]() . Вектор
. Вектор ![]() називають сумою векторів
називають сумою векторів ![]() і
і ![]() .
.
|
|
|
|
Алгоритм побудови суми векторів ![]() за правилом трикутника:
за правилом трикутника:
-
Від довільної точки відкладемо вектор, що дорівнює вектору
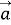 .
.
-
Від кінця вектора
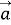 відкладемо вектор, що дорівнює вектору
відкладемо вектор, що дорівнює вектору 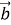 .
.
-
Сумою
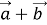 буде вектор, початок якого збігається з початком вектора
буде вектор, початок якого збігається з початком вектора 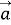 , а кінець з кінцем вектора
, а кінець з кінцем вектора 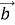 .
.
За правилом трикутника можна додавати вектори не користуючись малюнком. Наприклад: ![]() ,
, ![]() .
.
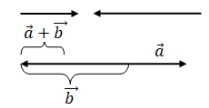
Колінеарні вектори також додаються за цим правилом:
|
|
|
Основні властивості додавання векторів:
-
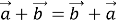 (переставний закон додавання);
(переставний закон додавання);
-
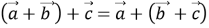 (сполучний закон додавання);
(сполучний закон додавання);
-
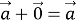 (закон додавання вектора до нульового вектора);
(закон додавання вектора до нульового вектора);
-
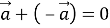 (закон додавання протилежних векторів).
(закон додавання протилежних векторів).
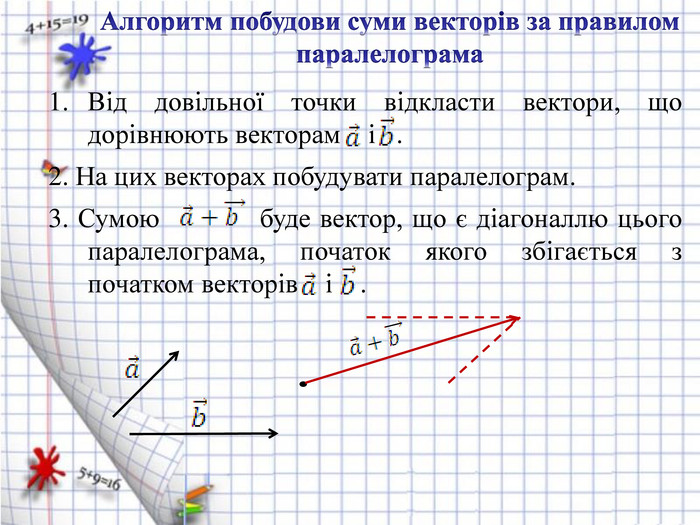
Правило додавання векторів (правило паралелограма):

Алгоритм побудови суми векторів ![]() за правилом паралелограма:
за правилом паралелограма:
-
Від довільної точки відкласти вектори, що дорівнюють векторам
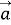 і
і 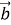 .
.
- На цих векторах побудувати паралелограм.
-
Сумою
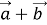 буде вектор, що є діагоналлю цього паралелограма, початок якого збігається з початком векторів
буде вектор, що є діагоналлю цього паралелограма, початок якого збігається з початком векторів 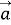 і
і  .
.
VІ. Закріплення вивченого.
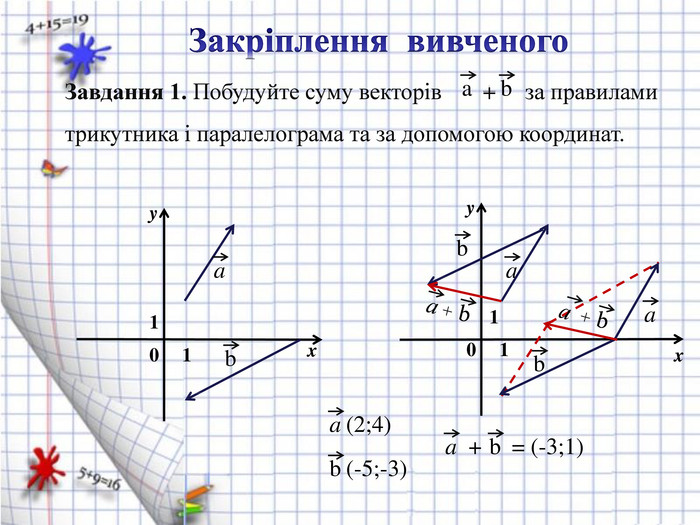
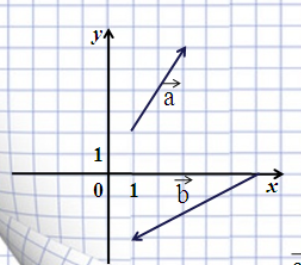
Завдання 1. Побудуйте суму векторів ![]() за правилами трикутника і паралелограма та за допомогою координат.
за правилами трикутника і паралелограма та за допомогою координат.
Завдання 2. № 500 (б, в) з підручника ст.. 160.
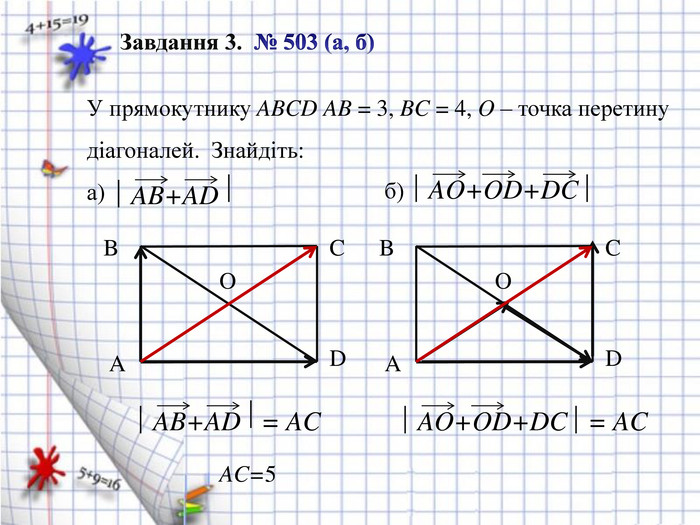
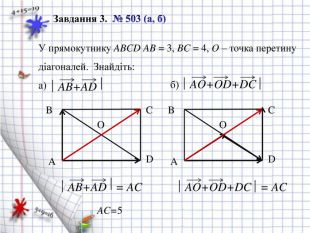
Завдання 3. №503 (а, б) з підручника ст.. 160.
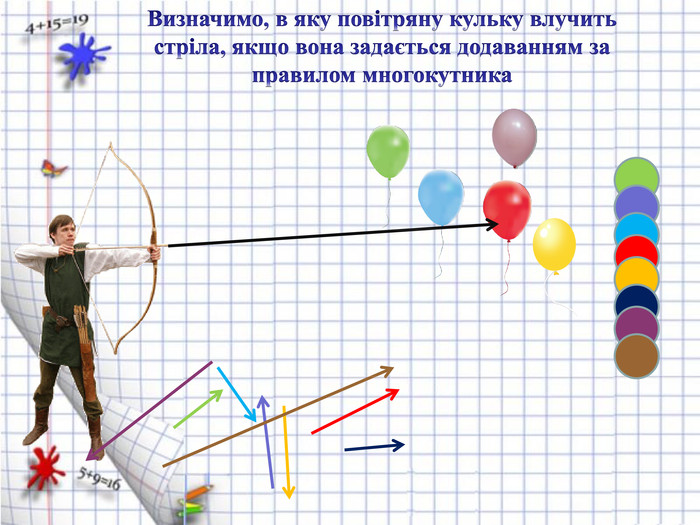
Завдання 4. (узагальнення)
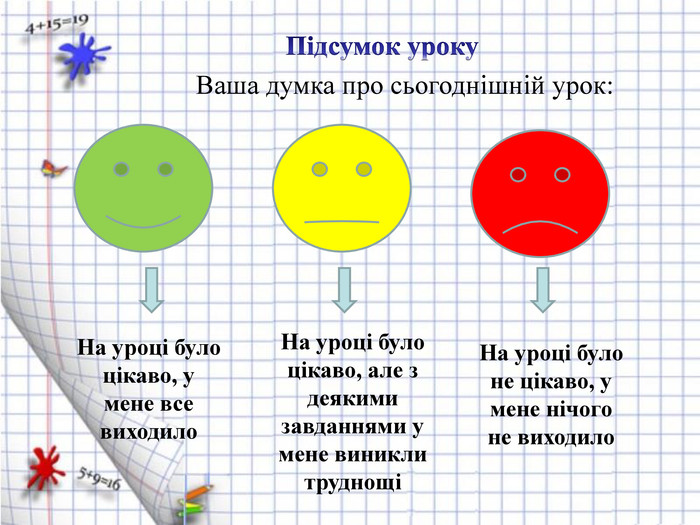
VІІ. Підбиття підсумків.
Рефлексія «Світлофор»

VІІІ. Домашнє завдання.
Опрацювати: § 15, п. 15.1 (стор. 154-156)
Виконати: № 489 (а), 502 (а), 504 (а, б)
-
-
Дякую за розробку!
-
Дякую вам за вашу роботу

про публікацію авторської розробки
Додати розробку