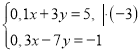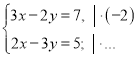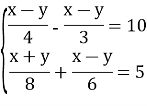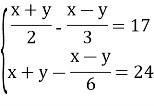Конспект уроку "РОЗВ’ЯЗУВАННЯ СИСТЕМ ЛІНІЙНИХ РІВНЯНЬ ІЗ ДВОМА ЗМІННИМИ СПОСОБОМ ДОДАВАННЯ",7 клас

РОЗВ’ЯЗУВАННЯ СИСТЕМ ЛІНІЙНИХ РІВНЯНЬ

ІЗ ДВОМА ЗМІННИМИ СПОСОБОМ ДОДАВАННЯ

 

Мета:

•     Навчальна:

•        формувати в учнів вміння і навички розв’язувати системи лінійних рівнянь з двома змінними способом додавання;
•        формувати навики самоконтролю та самоорганізації;

•     Розвивальна:

•        розвивати пам’ять, обчислювальні навички, увагу, самостійність при розв’язуванні вправ;

•     Виховальна:

•        виховувати культуру математичних записів, інтерес до математики;
•        виховувати спостережливість та охайність;

Тип уроку: урок формування вмінь і навичок.

Обладнання: мультимедійний проектор, ноутбук, картки із завданнями.

 

Хід уроку

І. Етап орієнтації

Перевірити готовність учнів до уроку.

Основні правила роботи на уроці.

Перевірка домашнього завдання.

2-є учнів по черзі біля дошки вставляють пропущені значення.

 

Усне опитування «Мікрофон»

1.Наведіть приклад і дайте означення лінійного рівняння з двома   змінними.

2.Що називають розв‘язком рівняння з двома змінними?

   Чи є пара чисел (4;1) розв‘язком рівняння х – 2y = 2?

3.Наведіть приклад системи рівнянь з двом змінними.

4.Що називають розв‘язком системи рівнянь з двома змінними?

5.Як розв‘язують систему двох лінійних рівнянь графічно?

6.Скільки розв‘язків може мати система двох лінійних рівнянь з двома змінними?

7.Як розв‘язують систему двох рівнянь з двома змінними способом підстановки?

8.Чи є пара чисел (-2;3) розв‘язком системи рівнянь:

 

 

     9.З рівняння 4х – y = 6 виразіть:

1. змінну х через змінну y;
2. змінну y через змінну х.

 

1.     Що називається системою лінійних рівнянь? (деяка кількість рівнянь, об'єднаних фігурною дужкою)
2.     Що називають розв’язком системи лінійних рівнянь з двома змінними? (пару значень змінних, для яких кожне рівняння системи лінійних рівнянь перетворюється в правильну числову рівність)
3.     Що означає «розв’язати систему лінійних рівнянь з двома змінними»? (означає знайти всі її розв’язки або довести, що розв’язків немає)
4.     Які системи лінійних рівнянь називаються рівносильними? (системи лінійних рівнянь із двома змінними, які мають одні й ті ж розв’язки)
5.     Скільки розв’язків може мати система лінійних рівнянь? (система лінійних рівнянь може мати один, безліч, жодного розв'язків)
6.     Які ви знаєте способи розв’язування системи лінійних рівнянь з двома невідомими? (графічний спосіб, спосіб підстановки та спосіб додавання)
7.     Як перевірити чи є пара чисел розв’язком системи лінійних рівнянь? (підставити цей розв’язок у систему і, якщо він задовольнятиме рівняння системи, тоді і буде він розв’язком даної системи)

 

ІІ. Етап мотивації

Розв’яжіть систему (відомим вам способом).

Зрозуміло, що спробувавши: а) побудувати графік; б) виразити одну змінну через іншу (з будь-якого рівняння), маємо певні труднощі (а) неточні побудови; б) незручність обчислень), тому свідомо доходимо висновку про необхідність подальшого вивчення питання про способи розв’язування та їх застосування під час розв’язування систем лінійних рівнянь із двома змінними (це і є мета й завдання уроку).

 

ІІІ. Етап планування

1. Вивчення способу додавання.
2. Напрацювання навиків розв’язування вправ.
3. Порівняльний аналіз всіх відомих способів розв’язання систем рівнянь.

 

IV. Етап організації і виконання плану діяльності.

1. Усні питання

1. Знайдіть НСК чисел: 1) 1 і 9; 2) 3; 7; 3) 3 і 6; 4) 6; 15; 5) 2; 5.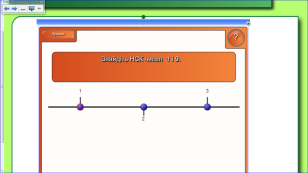

 

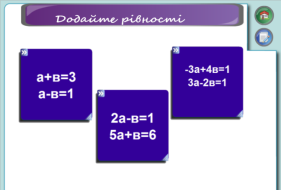
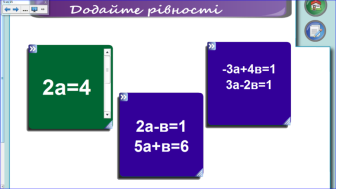
2. Додайте рівності:

1) та ; 2) ; ; 3) ; .

 

 

3. Розв’яжіть рівняння:

1) ;  2) ;  3) ;  4) ;  5) ; 6) .

4. Чи проходить через точку графік рівняння:

1) ; 2) ; 3) ; 4) ?

 

2. Вивчення нового матеріалу

Виведення алгоритму на прикладі.

Як і в попередній темі, вивченню способу додавання передує приклад, що на числових рівностях показує зміст тих рівносильних перетворень рівнянь системи, що передбачені алгоритмом розв’язування систем способом додавання. Як і на попередньому уроці зміст самого алгоритму пояснюємо на прикладі. Особливо звертаємо увагу на те, що цей спосіб є більш універсальний, бо для будь-яких значень коефіцієнтів при змінній, легко приводить до лінійного рівняння з однією змінною. Також звертаємо увагу на те, що п. 1 в алгоритмі може бути виконаний або повністю (множимо на числа обидва рівняння системи), або частково (множимо на число тільки одне рівняння системи).

Записи в зошитах можуть мати вигляд:

 

Конспект 24           Розв’язання систем лінійних рівнянь із двома змінними способом додавання
Алгоритм 1. Помножте обидві частини рівнянь (рівняння) системи на такі числа, щоб коефіцієнти при одній зі змінних стали протилежними числами	Приклад: 1. помножимо обидві частини 1-го рівняння на (–3); маємо систему:
2. Додайте почленно ліві й праві частини рівнянь	2.
3. Розв’яжіть здобуте рівняння з однією змінною	3. ;
4. Знайдіть відповідне значення іншої змінної	4. ; ; ; . Відповідь. (20; 1)

 

3.Прокоментувати розв’язання

Прокоментуйте розв’язання системи рівнянь способом додавання:

; ; ; ; ; .

Відповідь. (5; 3).

Який крок алгоритму в розв’язанні відсутній? Чому?

4.Робота з картками (додаток)

5.Робота з підручником (самостійно)

 

№ 986. Скільки розв’язків має система рівнянь залежно від значень коефіцієнта а?

6.Робота в групах

Розподіл на групи «Голосування ногами»

1. Яка точка лежить на осі Ох?

А) (5;0);

Б) (0;3);

В) (1;1).

2. Яка точка лежить на осі Оу?

А) (5;0);

Б) (0;3);

В) (1;1).

3. Яка точка лежить в І чверті?

А) (5;0);

Б) (0;3);

В) (1;1).

 

Повторити

• Які способи розв’язання системи ми знаємо?
• Алгоритм розв’язання кожного виду.

 

Завдання «Хто швидше»

Кожна група обирає собі спосіб розв’язання (витягує листочки). Виконуємо – хто швидше, але не довше 1  хвилини.

Розв’язати систему

1. .
2. .
3. 

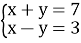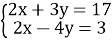Висновок: найзручніший спосіб -  додавання.

Вислови

 

Запам’ятай!

Людині, яка вивчає алгебру, часто корисніше розв’язати одну і ту саму задачу трьома і більше способами, ніж  розв’язати три-чотири різні задачі.

* * *

 

Розв’язуючи задачу різними способами, можна шляхом порівняння з’ясувати, який з них коротший та ефективніший. Так набувається досвід.

У. Сойєр.

 

 

V.  Етап контрольно-оцінюючий.

1. Отже, наш урок закінчується. Тому давайте ще раз пригадаємо алгоритм розв’язування системи лінійних рівнянь способом додавання.

 

Алгоритм:

•   Зрівняти модулі коефіцієнтів при будь-якій змінній.
•   Додати почленно рівняння системи.
•   Розв'язати нове рівняння і знайти значення однієї змінної.
•   Підставити значення знайденої змінної в інше рівняння і знайти значення другої змінної.
•   Записати відповідь: (х; у).

2. Позначити точки на координатній площині.

Ряд точок (утворюється форма яйця)

Символом якого свята є яйце? – відео про писанки.

Побажання від священника!

 

3. Вправа «Відгадай слово»

1) При якому значенні а графік рівняння 2х + ау = 4 проходить через точку    (1; 2)?

      а)  2;             б) 0;           в) 1;           г) -1?                                         (А)

____________________________________________________________________________________________________________________________________________________________________________________________________________

 

2) Знайдіть розв’язок системи рівнянь:

____________________________________________________________________________________________________________________________________________________________________________________________________________

 

     к) (3; 11);          л) (11; 3);         м) (-11; 3);           н) (-3; 11)        (Л)

 

3) Знайдіть розв’язок системи рівнянь: 

____________________________________________________________________________________________________________________________________________________________________________________________________________

 

    а) (3; 3);            б) (1; 3);              в) (1; -3);            г) (-1; 3)           (Г)

4) Знайдіть розв’язок системи рівнянь: 

____________________________________________________________________________________________________________________________________________________________________________________________________________

 

    г) (-1; -1);         д) (1; 1);               е) (5; 5);           і) (-5; -5)            (Е)

5) При яких значеннях а система рівнянь      має безліч розв’язків?

____________________________________________________________________________________________________________________________________________________________________________________________________________

 

    а) 4;             б) -5;         в) 2;         г) 3                                               (Б)

 

6) Сума двох чисел 21, при чому одне з них на 5 більше за друге. Знайдіть ці числа. Яка система рівнянь відповідає умові задачі? ____________________________________________________________________________________________________________________________________________________________________________________________________________

 

     о) ;       п) ;       р) ;        с) (Р)

 

7) Знайдіть координати точки перетину графіків рівнянь 2х – 3у = 16   і    

 х + 2у = 1.

     а) (5; -2);       б) (-2; 5);            в) (2; -5);             г) (-5; -2)                   (А)

____________________________________________________________________________________________________________________________________________________________________________________________________________

 

Оцінювання.

 

Домашнє завдання.

 

Рефлексія.  Розмістити писанки в кошики.

 

 

Картка роботи учня _________________________ Дата _________

Основна частина		Додаткова частина			Оцінка
1	Розв’язання:	1	Розв’язання:
2	Розв’язання:	2	Розв’язання:
3	Розв’язання:	3	Розв’язання:
4	Заповніть пропуски, щоб запис став правильним: Відповідь. (...; ...).
5	Завдання ІІ рівня Розв’язання:	5		Завдання ІІ рівня Розв’язання:
6	Завдання ІІІ рівня Розв’язання:	6		Завдання ІІІ рівня   Розв’язання:

Самооцінка учня ________________ Оцінка вчителя _________________