Конспект уроку "Синус, косинус, тангенс кутів від 0° до 180°"

Урок №4. Тема:  Синус, косинус, тангенс кутів від 0° до 180°

Формування компетентностей:

предметна компетентність:

• сформувати поняття синуса, косинуса, тангенса кутів від 0° до 180°;
• розвивати уміння знаходити тригонометричні функції тупих кутів;

ключові компетентності:

• спілкування державною мовою – уміння доречно та коректно вживати в

мовленні математичну термінологію, чітко, лаконічно та зрозуміло формулювати думку; поповнювати свій словниковий запас;

• математична компетентність – уміння оперувати числовою інформацією;
• уміння вчитися впродовж життя – уміння оцінювати результати своєї

навчальної діяльності.

Тип уроку: комбінований.

Обладнання та наочність: підручник з геометрії за 9 клас, автори: Мерзляк, Полонський, Якір, 2017 р.

Хід уроку

I. Організаційний момент.

• Налаштовування на роботу.
•   Перевірка домашнього завдання: повідомлення балів за пройдений тест і розбір типових помилок.

II. Актуалізація опорних знань.

Фронтальне опитування

1. Сформулюйте означення синуса, косинуса, тангенса гострого кута прямокутного трикутника.
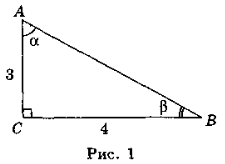
2. Знайдіть за рис. 1 sinα, cosα, tgα, cosβ, sinβ, tgβ.
3. Як пов'язані sinα і cosα, якщо α — гострий кут прямокут­ного трикутника?
4. Якою залежністю пов'язані sinα, cosα, tgα?

Мотивація навчальної діяльності учнів

Ви знаєте означення синуса, косинуса і тангенса гострого кута прямокутного трикутника. А чи можна знайти, наприклад, sin120° або cos180° ? (Відповідь: так.) Сьогодні ви вивчите означення синуса, косинуса, тангенса кутів від 0° до 180°.

План вивчення нового матеріалу

1. Означення синуса, косинуса і тангенса кутів від 0° до 180°.
2. Знаходження значень синуса, косинуса і тангенса тупих кутів.

Опорний конспект

Означення синуса, косинуса і тангенса кутів від 0° до 180°

Побудуємо коло з центром у початку координат і радіусом 1 (рис. 2). Таке коло називається одиничним. Побудуємо гострий кут а, який утворює радіус ОА цього кола з додатним напрямом осі Ох. Нехай точка А має координати (х; у). Тоді для прямокутного трикутника АОВ маємо:

sinα = = = у;  cosα = = = x;  tgα = = .

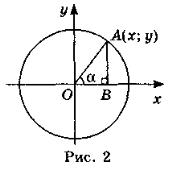
Таким чином: синусом кута α є ордината точки А одиничного кола, причому радіус ОА утворює з додатним напрямом осі Ох кут α. Косинусом кута α є абсциса точки А одиничного кола, причому радіус ОА утворює з додатним напрямом осі Ох кут α. Тангенсом кута α є відношення ординати точки А до абсциси цієї точки, причому радіус ОА утворює з додатним напрямом осі Ох кут α.

Знаходження значень синуса, косинуса і тангенса тупих кутів

Користуючись наданими означеннями, дамо означення для будь-якого кута α, 0° < α < 180°. Тоді sin 0° = 0, cos 0° = 1, tg 0° = 0; sin 180° = 0,

cos 180° = -l,    tg 180° = 0.

Якщо кут α — тупий (0° < α < 90°), то ордината точки А (рис. 3) додатна (тобто sin α > 0), абсциса — від'ємна (тобто cosα < 0), і відношення ординати до абсциси — від'ємне (тобто tgα < 0).

Отже, косинус, тангенс тупого кута від'ємні.

Якщо α – тупий кут (рис. 4), то cos α = ОС = - OD = -cos (180°- α),

sinα = AC = AD = sin (180° - α), тоді tg α = = - = -tg(180° - α).

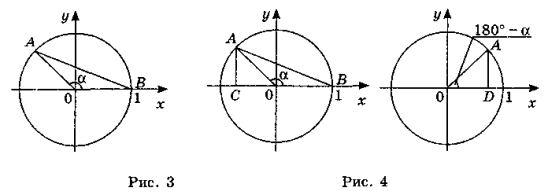
Отже, щоб знайти синус тупого кута, досить знайти синус суміжного кута; щоб знайти косинус, тангенс тупого кута, треба знайти число, протилежне косинусу, тангенсу суміжного кута.

Наприклад, sin 120° = sin (180° - 120°) = sin 60° = ,

cos 150^o = - cos (180° - 150°) = - cos 30° = - ,

tg 135° = -tg (180° - 135°) = - tg 45° = - 1.

Якщо учні класу мають недостатню математичну підготовку, то можна спростити пояснення. Досить сказати, що синус тупого кута дорівнює синусу суміжного кута, а косинус і тангенс тупого кута дорівнюють числу, протилежному косинусу і тангенсу суміжного кута.

Синус 0° дорівнює 0, синус 180° дорівнює 0, синус 90° дорівнює 1; а косинус 0° дорівнює 1, косинус 180° дорівнює -1, косинус 90° дорівнює 0; тоді тангенс 0° і 180° дорівнюють 0, а тангенс 90° не існує.

IV. Засвоєння нових знань і способів дій

№ 1.2. Чому дорівнює:

1) sin якщо

2) cos якщо ;

3) cos якщо

4) якщо ?

№1.4.  Знайдіть значення виразу:

1)

2)

3)

4)

5)

6) .

№1.6. Чому дорівнює синус кута, якщо його косинус дорівнює:

1) 1;            2) 0?

№1.8. Знайдіть

V. Підбиття підсумків уроку, рефлексія

В ході фронтального опитування разом з учнями підвести підсумки уроку. Запропонувати наступні питання:

1. Дайте означення синуса, косинуса, тангенса кутів від 0° до 180°.
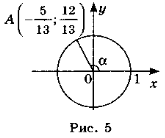
2. Користуючись рис. 5, знайдіть:

а) sin α; б) cos α; в) tg α.

VI. Домашнє завдання
(§1 п.1 № 1.3, 1.9)