Конспект уроку та презентація з геометрії для 8-го класу на тему Теорема Піфагора"

КЗ «БОГОДУХІВСЬКА ЗОШ І-ІІІ СТУПЕНІВ №2»

 

 

 

Урок математики  у 8 класі –

урок однієї теореми

 

 

 

 

 

 

„К Р О К У Ю Ч И

 

З А     П І Ф А Г О Р О М”

 

 

       Підготувала:

       учитель математики

       Зубова В.Б.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Мета:

• Сформувати в учнів розуміння змісту теореми Піфагора та її доведення.
• Формувати вміння відтворювати зміст теореми Піфагора та навички знаходження різних способів її доведення.
• Застосовувати набутих знань у практичній діяльності.
• Сприяти розвитку математичних здібностей школярів; через перегляд презентації та розгадування кросворда посилити цікавість учнів до математики.
• Удосконалювати навички колективної роботи, цілеспрямованості, відповідальності, активності, спостережливості, кмітливості.
• Розвивати пізнавальну та інформаційну компетентності, компетентність продуктивної творчої діяльності.

 

Вступне слово вчителя.

► Урок ми почнемо з розгадування кросворда, щоб дізнатись прізвище великого математика, з біографією якого ми сьогодні ознайомимося, вивчимо та доведемо теорему, названу його ім’ям.

Отож давайте разом розгадаємо кросворд.

         (слайди 1-3)

Кросворд

 

 

7	1				П
			2        4		І
				3	Ф
					А
				5	Г
	6				О
					Р

 

 

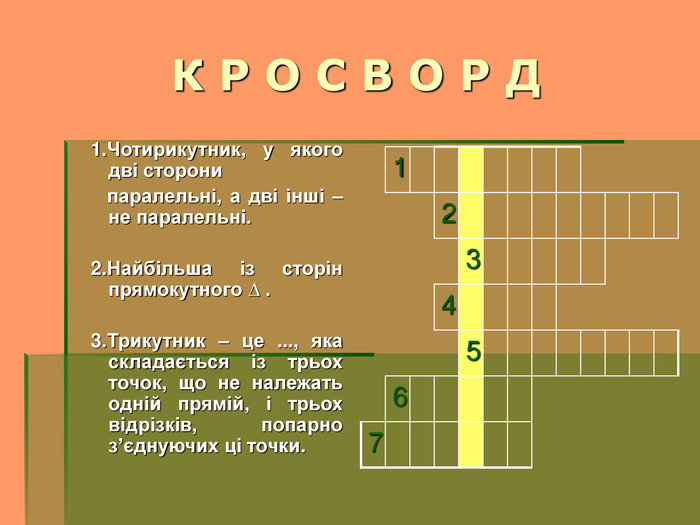
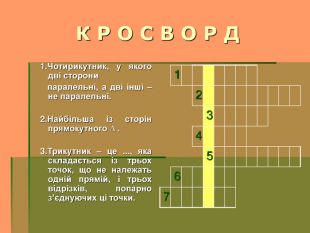
1.Чотирикутник, у якого дві сторони паралельні, а дві інші – не паралельні.

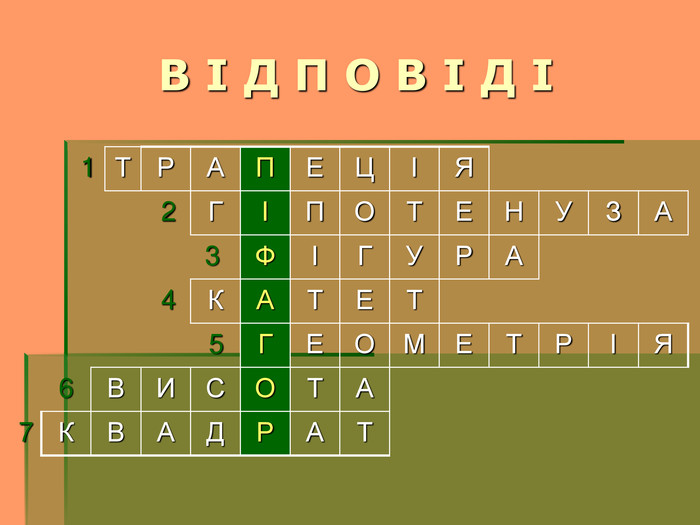
           (Трапеція)

 

2.Найбільша із сторін прямокутного трикутника.   (Гіпотенуза)

 

3.Трикутник – це ..., яка складається із трьох точок, що не належать одній прямій, і трьох відрізків, попарно з’єднуючих ці точки.                            (Фігура)

 

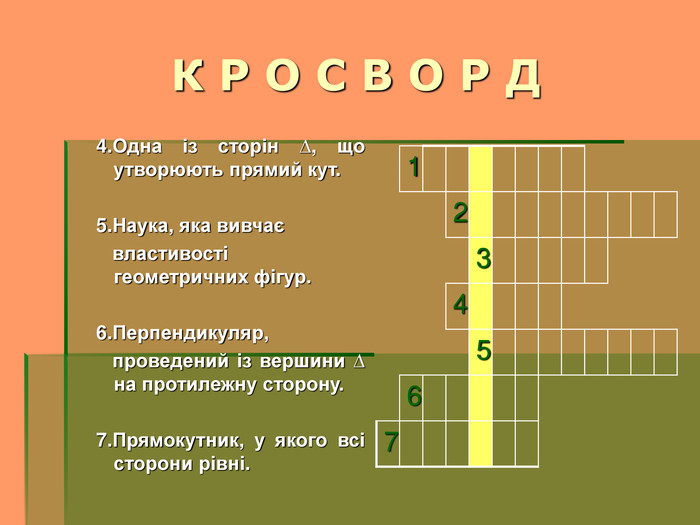
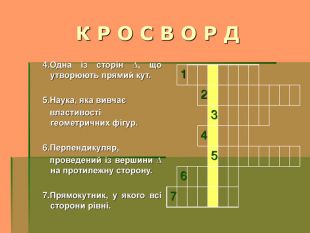
4.Одна із сторін трикутника, що утворюють прямий кут.  (Катет)

 

5.Наука, яка вивчає властивості геометричних фігур.   (Геометрія)

 

6.Перпендикуляр, проведений із вершини трикутника на протилежну сторону.                                                                                                                                                                                                                                                                                                                                  (Висота)

 

7.Прямокутник, у якого всі сторони рівні.    (Квадрат)

Слайд 4

► Теорема Піфагора – одна з основних у евклідовій геометрії. Завдяки їй можна довести та розв’язати не одну задачу. Тому її потрібно добре засвоїти.

Сьогодні у нас урок однієї теореми, на якому ми познайомимося з різними способами її доведення (а відомо понад 300 різних доведень), використовуючи для цього знання із різних розділів геометрії; розв’яжемо декілька задач на використання цієї теореми.

Слайд 5

А епіграфом нашого уроку пропоную взяти наступні слова великого Піфагора:

“Не вважай  себе  великою  людиною  за розміром твоєї тіні під час заходу  Сонця.” 

         

► Напередодні нашого уроку деякі учні вашого класу отримали завдання, використовуючи додаткову літературу та Інтернет-ресурси, підготувати довідку із біографії Піфагора, яку зараз ми заслухаємо:

 

Із біографії Піфагора   (слайди 6-12)

• Відомий древньогрецький філософ і математик Піфагор Самоський народився на острові Самос, далеко від Греції в 576 році до н. е.
• За порадою Фалеса 22 роки Піфагор набирався мудрості в Єгипті. Під час завойовницьких походів на Єгипед Піфагор потрапив у полон і його рпродали у рабство. Так він опинився у Вавілоні. Там він виавчав древню культуру і досягнення науки різних країн. Після повернення додому, він поселився в Італії, а потім у Сицілії.

 

• Піфагор – це не ім’я, а прізвисько, яке дали йому за те, що він висказував істину постійно, як оракул. “ Піфагор” – означає “ переконуючий мовою”.
• Після першої прочитаної ним лекції Піфагор зібрав 2000 учнів і створив школу філософів та математиків.

Школа Піфагора – це організація зі строго обмеженим числом учнів із аристократії,

     і  потрапити туди було не просто. За  твердженням деяких істориків, одним  із таких іспитів була  п’ятирічна обітниця  мовчати, і весь цей час учні могли слухати голос учителя через завісу, а побачити його могли лише тоді, коли „їхні душі  будуть очищені музикою і таємницею гармонії чисел”.

В Піфагоровій школі багато уваги приділялося музиці, живопису, фізичній культурі. Відомо, що Піфагор чотири рази був Олімпійським чемпіоном.

 Учитель.

Піфагорівцями було зроблено багато наукових відкриттів. Одне із самих важливих – це теорема Піфагора.  Довгий час вважалося, що до Піфагора ця теорема біла невідома. Та в теперішній час було встановлено, що ця важлива теорема зустрічалася  у вавілонських текстах, написаних за 1200 років до Піфагора.

 

► А зараз пропоную вам провести експеримент – ви отримуєте мотузку із 12 вузлами. Вам необхідно буде утворити трикутники із сторонами 3,4 і 5 рівних відрізків та визначити вид даних трикутників.

 

Слайд 13

Ще  в  Давньому  Єгипті  була відома  теорема, яка потім дістала  назву  „ТЕОРЕМА  ПІФАГОРА”.

 

Вона застосовувалась тоді для побудови  прямих   кутів  на місцевості за допомогою мотузки з вузликами, яку натягували у вигляді трикутника зі сторонами 3,4 і 5 вузлів.

 

Звідси і походить назва давніх землемірів – „гарпедонапти” - натягувачі мотузок.

 

Та заслуга Піфагора в тому, що він першим її довів.

     

У Франції і деяких областях Німеччини в середні віки цю теорему називали „ослиним мостом”, тому що доведення її було величезною перешкодою, так званим мостом, перейти  який могли тільки розумні учні.

У математиків арабського Сходу ця теорема одержала назву „теореми нареченої”. Справа в тому, що в деяких списках „Начал” Евкліда ця теорема називалася „теоремою німфи” за подібність креслення з метеликом, що грецькою звався німфою. Але цим словом греки називали деяких богинь, а також наречених. При перекладі арабський перекладач, не звернувши уваги на креслення, перевів слово „німфа” як „наречена”, а не „метелик» , – так з’явилась назва „теореми нареченої”. А відома всім школярам назва „Піфагорові штани” виникла через схожість креслення до Евклідового доведення теореми Піфагора зі штанами.

 

Давайте зараз познайомимось із змістом теореми Піфагора.

 

Слайди 14-15

Існує понад 300 різних варіантів доведення теореми Піфагора. Із декількома ми зараз в вами познайомимося.

 

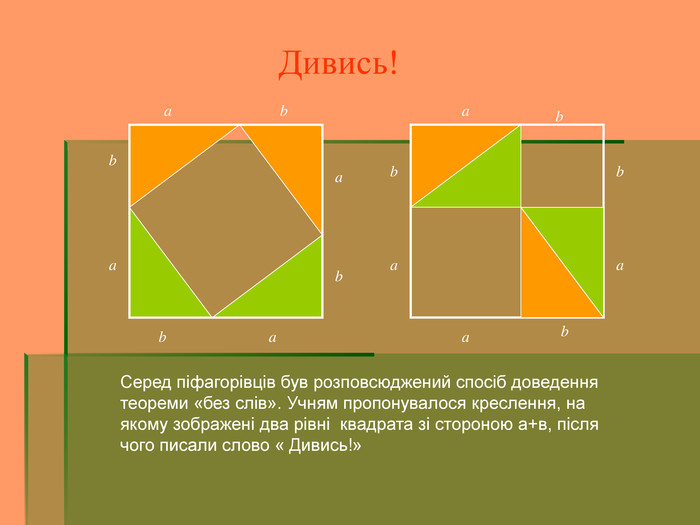
1. Серед піфагорівців був розповсюджений спосіб доведення теореми «без слів». Учням пропонувалося креслення, на якому зображені два рівні  квадрата зі стороною а+в, після чого писали слово « Дивись!»

 

Слайд 16

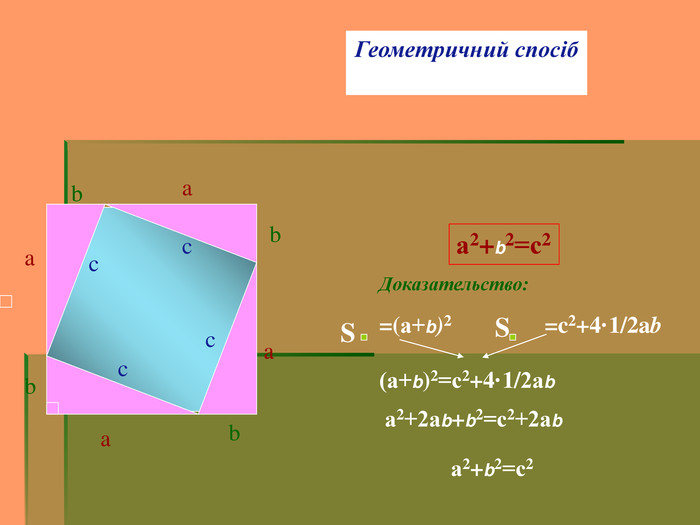
2. Геометричний спосіб.

Слайд 17

 

3. Доведення із підручника на ст..140.

 

► Застосування теореми Піфагора

 

Розв’язування задач із підручника №1, №2 ст.143

(слайди 18-19)

 

►Це цікаво знати!

Слайди 20-23

 Вірші про теорему Піфагора

 

Відкриття теореми Піфагора оточено ореолом красивих легенд. Розповідають, що він на честь цього відкриття приніс у жертву бика, а у деяких легендах один бик перетворився на цілу сотню биків.

Хочу продекламувати сонет Шаліссо:

Пребудет вечной истина, как скоро

Её познает слабый человек!

И ныне теорема Пифагора

Верна, как и в его далекий век.

 Обильно бело жертвоприношенье

 Богам от Пифагора. Сто быков

 Он отдал на закланье и сожженье

 За света луч, пришедший с облаков.

  Поэтому всегда с тех самых пор,

  Чуть истина рождается на свет,

  Быки ревут, её почуяв, вслед.

  Они не в силах помешать,

  А могут лишь, закрыв глаза, дрожать

  От страха, что вселил в них Пифагор.

          (слайди 18-19)

 

 

► Рефлексія (слайд 24)

Підсумок уроку.

Доказів теореми Піфагора дуже багато й вони відкриваються дотепер, так що не сумуйте, може ви знайдете ще один доказ ...

 

Слайд 25

 

► Домашнє завдання:

1. Придумати або знайти в додатковій літературі задачу практичного змісту на застосування теореми Піфагора.

2. Вивчити Теорему Піфагора та її доведення

    Розв’язати №1 (б) та №2 (б) ст.. 143